Irrungen und Wirrungen in einem gestaltlosen Universum – Lotto Tipps Teil 1

Die Erforschung einer elastischen Welt
Die Antriebskraft einer mathematischen Entdeckung ist nicht logisches Denken, sondern Vorstellungsvermögen.
Auguste De Morgan

Offensichtlich … Binden Sie Ihre Fußgelenke mit einem 1,5 Meter langen Strick zusammen. Schlurfen Sie in die Intimsphäre Ihres Schlafzimmers. Lassen Sie jetzt, ohne den Strick zu entfernen, Ihre Hosen fallen und versuchen Sie dann, sie verkehrt herum wieder anzuziehen. Natürlich scheint so ein Kunststück einfach nur unmöglich zu sein. Selbst ein Entfesselungskünstler wie Houdini müsste daran scheitern.

Überraschung… Man kann diesen Trick mit der umgestülpten Hose tatsächlich vorführen. Sie können Ihre Hose ziehen und zerren, bis sie schließlich ordentlich Ihre Waden bedeckt, der Reißverschluss sich in ganzer Pracht präsentiert und die Hosentaschen an Ihren Hüften wedeln. Diese alberne Übung passt wie maßgeschneidert als Einleitung für die erstaunliche, elastische Realität in einer Welt aus Gummi.

Man kann sich nur wundern
Wie oft müssen wir uns anhören, wir sollen flexibel sein. Während manch einer sich diesen Rat zu Herzen nimmt und einen Yogakurs belegt, besteht unser Ziel darin, eine gewisse geistige Beweglichkeit zu entwickeln. In diesem Kapitel wollen wir die Flexibilität auf die elastische Spitze treiben und ein Universum erforschen, in dem alles, was wir berühren und sehen, vollkommen formlos ist.

Eine brauchbare Methode, um einen kreativen Einfall nach dem anderen zu produzieren, besteht darin, uns vorzustellen, dass ein paar subtile Merkmale unserer Alltagswelt geringfügig verändert sind und wir dann diesen veränderten Zustand untersuchen. Welche Eigenschaften bleiben gleich, und welche sind anders? Die Erforschung einer hypothetischen Welt erzeugt ganze Galaxien neuer Ideen. So werden wir ein synergetisches Zusammenspiel entdecken, in dessen Verlauf uns diese neuen Vorstellungen zu frischen Einsichten in unsere vertraute Alltagswelt anregen werden.

Spaß mit Gummi – exotische Abenteuer mit einer Gummifolie
An dieser Stelle wollen wir auf unseren eigenen Rat hören und uns ein Universum mit einer winzigen Abänderung vorstellen: Ein jeglicher Teil unserer stofflichen Welt soll extrem verzerrbar sei. Das heißt, jedes Objekt besteht aus einer unrealistisch biegsamen, gummiartigen Substanz, die grenzenlos elastisch ist. Daher lässt sich jedes Objekt beliebig dehnen, biegen, zusammendrücken, erweitern und ganz allgemein formen. In diesem Reich können wir einen Basketball zur Größe des Mondes aufblasen oder einen Dirigentenstab so weit biegen und dehnen, dass er aussieht wie der berühmte Torbogen von Saint Louis, oder einen Geldschein beliebig vergrößern. Diese anscheinend alberne Phantasie über eine elastische Realität gehört zu einem Gebiet der Mathematik, das als Topologie oder inoffiziell als Gummifoliengeometrie bekannt ist.

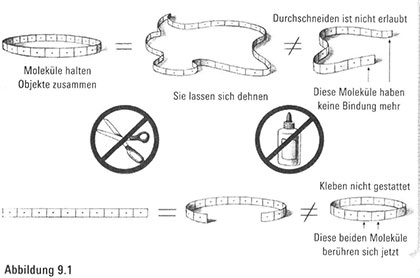
Natürlich hätte dieses hypothetische Reich ohne gewisse Einschränkungen keine interessanten Eigenschaften – denn ließe sich alles einfach in eine strukturlose Brühe auflösen, blieben auch keine diskussionswürdigen Unterschiede übrig. Stattdessen stellen wir uns vor, die Objekte jener Welt bestünden aus Molekülen, die mit benachbarten Molekülen verbunden seien, und wenngleich die Moleküle gedehnt, geschrumpft und verrenkt werden könnten, blieben die Bindungen erhalten, und es kämen keine neuen Bindungen hinzu. Folglich ließen sich die Gegenstände dehnen und verzerren, aber nicht zerschneiden oder verkleben. Denn würde man ein Objekt zerreißen, ginge irgendeine Bindung verloren. Und wenn wir beispielsweise einen Kreis erzeugten, indem wir die beiden Enden eines Linienabschnitts zusammenklebten, käme eine Verbindung zustande, die zuvor nicht existierte (Abbildung 9.1).

Um eine Vorstellung zu entwickeln, was auf erlaubte Art und Weise in diesem Gummireich verwirklicht werden kann und was nicht, wollen wir eine Aufwärmübung mit flexiblen Schriftarten machen. Welche Buchstaben des Alphabets können umgeformt werden, um einander zu ähneln? Entscheidend bei dieser Übung ist die Schriftart, sodass wir serifenlose nehmen (ohne die kleinen horizontalen Striche). Folglich lässt das S sich so verdrehen, dass es aussieht wie ein C. I, J, M, N, U.V, W und ein z. All diese Buchstaben sind lediglich Verzerrungen einer Linie – durch Verrenkung dieser Linie können wir jede beliebige Kurve, Biegung und jeden Winkel erzeugen. Gleichfalls ist das o dasselbe wie das D. Eine andere Buchstabengruppe besteht aus E, F, T und Y. Sie alle können gebogen und gedehnt werden, um so auszusehen wie jeder andere Buchstabe in der Gruppe (Abbildung 9.2). Betrachten wir die Welt aus dieser neuen Perspektive, fragen wir uns, welche Objekte oder Figuren sich dehnen, schrumpfen, biegen oder sonst wie verzerren lassen und bei welchen Gegenständen uns das nicht gelingt.

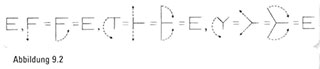
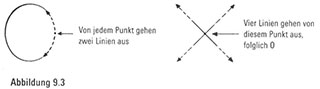
So kann beispielsweise der Buchstabe 0 nicht so umgeformt werden, dass er dem x ähnelt, weil das x einen Punkt hat, von dem vier Linien ausgehen, während von jedem Punkt auf dem Kreis nur zwei Linien ausgehen (Abbildung 9.3). Ganz gleich, wie sehr wir das x auch dehnen, der Punkt, von dem die vier Linien ausgehen, wird immer vier (wenn auch möglicherweise gekrümmte) Linien aufweisen.

Die Betrachtung der Welt aus dieser verzerrten topologischen

Perspektive ist zumindest einigermaßen unterhaltsam, aber sind wir denn tatsächlich schon davon überzeugt, dass dieser elastische Standpunkt irgendeine Bedeutung für unseren Alltag hat? An dieser Stelle wollen wir diese Angelegenheit vorerst auf sich beruhen lassen und stattdessen die Herausforderung dieser nervenden Metallpuzzlespiele annehmen, die in Kneipen herumliegen.

Kneipenpuzzles
Sogenannte Kneipenpuzzles aus Metall, die so aussehen, als hätte sie ein Hufschmied zurechtgebogen, sind unglaublich frustrierend. Da sollen wir also einen daran befestigten Ring entfernen, eine Holzkugel an einer Kette durch ein Loch schieben, das offensichtlich zu klein ist, oder andere Puzzleelemente so Zusammenlegen, dass eine Lösung unmöglich erscheint. Also nehmen wir eines dieser Puzzles auf eigenes Risiko zur Hand. Gelingt es uns nicht, es zu lösen, kriegen wir vor Verlegenheit und natürlich vom Bier einen roten Kopf – was für ernüchternde Aussichten!

Tatsächlich lassen sich diese lästigen Kneipenpuzzles lösen. Dafür müssen wir allerdings ein paar äußerst kreative Spielzüge wagen – als ersten Schritt schieben wir das Bierglas außer Reichweite. Aber was geschähe, wenn wir Topologen wären und diese Puzzles aus dehnbarem Gummi statt aus gnadenlosem Metall gefertigt wären? Dann geriete die Lösung zu einer einfachen Angelegen heit.

Interessanterweise kann uns die Übung, eine Gummiversion des Puzzles zu lösen, auf ein Manipulationsverfahren bringen, das beim unbiegsamen Metall zum gleichen Ziel führt. Schauen wir uns ein Beispiel an.

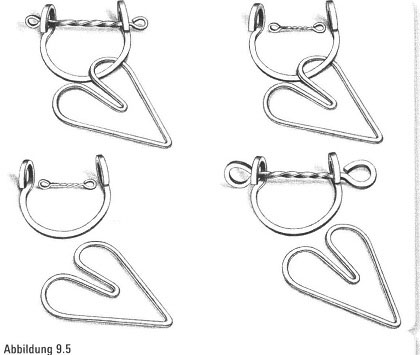
Um das Puzzle in Abbildung 9.4 zu lösen, müssen wir den herzförmigen Ring entfernen. Welche Schritte würden wir unternehmen, wenn das Puzzle aus Gummi und nicht aus Metall gemacht worden wäre? Wir würden einfach die Metallstange schrumpfen und so Vorgehen, wie es in Abbildung 9.5 gezeigt wird. Jetzt ist die Lösung ganz einfach. Wir können ohne weitere Verbiegungen den Ring entfernen. Und so lautet der Dreh: Wir stellen uns vor, die gleiche Folge von Schritten (mit Ausnahme des Schrumpfens) am unverformten Metallpuzzle zu unternehmen, und fragen uns, ob wir den Ring dazu bringen können, den Schritten zu folgen, die wir machen müssen, wenn wir unsere verzerrte Lösung wieder gerade biegen. Wir sehen, dass es funktioniert (Abbildung 9.6), und erkennen folglich, dass die Kneipenpuzzles zu Wachs in unseren Händen werden, wenn wir nur flexibel genug denken.

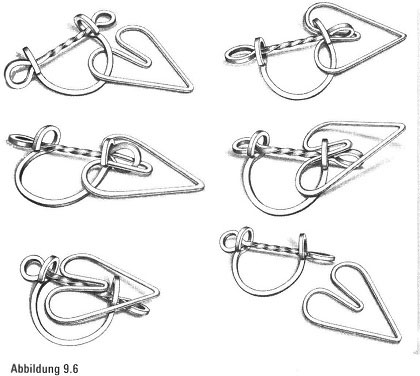
(Wir müssen allerdings gestehen, dass wir die Lösung für manche dieser Puzzles selbst im nüchternen Tageslicht und bewaffnet mit unseren flexibelsten Gedanken für fast unmöglich halten.)

Schneidertricks-Gummiunterwäsche und Hosen runterlassen
Wenden wir dieses flexible Denken nun auf unsere Kleidung an, finden wir provokative Alternativen zu unseren konventionellen Ausziehmethoden. Fangen wir mit folgender Frage an: Ist es möglich, eine ausreichend dehnbare Unterhose auszuziehen, ohne dafür die Hose ablegen zu müssen? Wollten wie hier eine kurze Antwort verraten, könnten einige vornehme Leser dies als geschmacklos betrachten. Allerdings müssen wir im Namen der Mathematik die Herausforderungen annehmen, wo immer sie uns begegnen mögen. Vielleicht möchten ja die wagemutigeren und weniger bescheidenen Leser die topologische Herausforderung annehmen und die Lösung seihst herausfinden, bevor sie weiterlesen.

Es ist tatsächlich möglich, Gummiunterhosen auf diese ab-sonderliche Art und Weise auszuziehen, wobei wir die Kneipenpuzzlemethode anwenden können, um zu verfolgen, wie es funktioniert. Zuerst nehmen wir an, unser linkes Bein sei aus Gummi und kann dramatisch auf fünf Zentimeter Länge zusammengedrückt werden (Abbildung 9.7). Danach lässt sich eine nicht dehnbare Unterhose einfach unter den Fuß unseres neuen, kurzen Beins ziehen. Und anschließend könnten wir sie am rechten Bein herunterfallen lassen (Abbildung 9.8). Mit dieser (möglicherweise beunruhigenden) Lösung eines linken Gummibeins im Hinterkopf, können wir uns inzwischen vorstellen, wie wir die Unterhose über das linke Bein in seiner normalen, ganzen Länge gestreift bekommen, weil nun ja die Unterhose dehnbar sein soll.

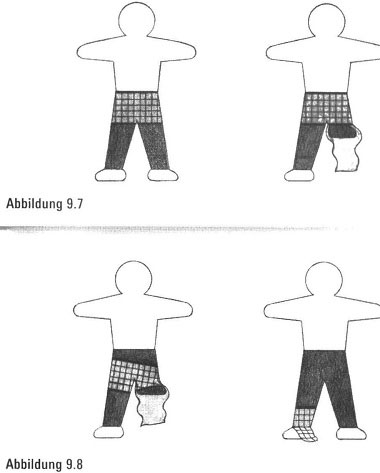
Mit der Entdeckung dieser Strategie, Gummiunterwäsche auszuziehen, wollen wir zeigen, wie man durch Konzentration auf die wesentlichen und durch Verzicht auf die oberflächlichen Merkmale eines Problems – seien sie nun topologischer, persönlicher oder gar politischer Natur – zu neuen Einsichten und Durchbrüchen gelangen kann, die sonst überhaupt nicht möglich gewesen wären. Andererseits hat das Verbergen unserer Unterwäsche auch einen gewissen Reiz.

Zu Beginn des Kapitels haben wir den Vorschlag gemacht, unsere Fußgelenke mit einem 1,5 Meter langen Strick festzubinden und dann, ohne den Strick zu lösen, unsere Hose auszuziehen und sie links herum wieder anzuziehen. Dieses Umwenden der Kleidung lässt sich tatsächlich mit richtigen Hosen durchführen.

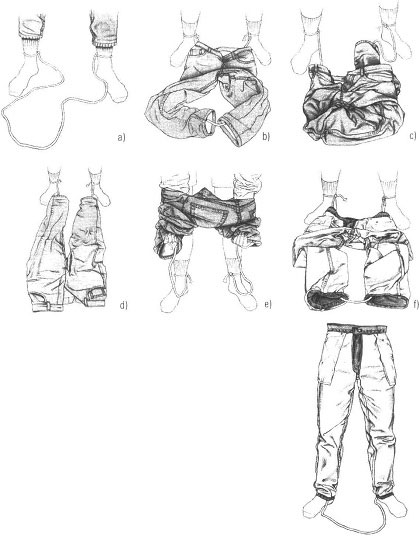
Abbildung 9.9:
a) Knoten Sie den Strick an Ihre Fußgelenke.
b) Ziehen Sie Ihre Hose über den Strick.
c) Ziehen Sie ein Hosenbein in voller Länge durch das andere Hosenbein.
d) Die Hose liegt jetzt mit der richtigen Seite nach oben, aber in verkehrter Richtung.
e) Greifen Sie hinein, umklammern Sie den Hosenaufschlag und ziehen Sie die Hosenbeine hoch.
f) Jetzt ist die ganze Hose links herum.

Dafür ist keine Annahme unrealistischer Elastizität erforderlich – glücklicherweise können wir unsere Stretchhosen im Kleiderschrank lassen. Die beste Strategie zur Lösung des Rätsels ist immer noch der Selbstversuch, obwohl der nicht gerade einfach ist. Wir empfehlen Ihnen dringend, sich ins Kampfgetümmel zu stürzen, bevor Sie einen Blick auf Abbildung 9.9 werfen, die die richtigen Schritte zeigt.

Hat die Erde wirklich die Form eines Donutst
Wir wollen jetzt unser Blickfeld von der Enge unserer Ankleideräume auf die Herrlichkeit der ganzen Welt erweitern. Wir wissen, dass die Erde eine Kugel ist. Wenn unsere Welt aber ungeheuer dehnbar wäre, hätten wir eine völlig andere intuitive Vorstellung davon, welche Formen miteinander übereinstimmten. Eine kugelförmige Welt und eine bananenförmige Welt wären dann ein und dasselbe, weil man eine Kugel dehnen und zerren kann, bis sie einer Banane ähnelt (Abbildung9.10). Aber selbst eine sagenhaft flexible, elastische Welt hätte noch ein paar Einschränkungen und Grenzen. So lässt sich beispielsweise, wie wir mathematisch beweisen werden, ein Donut nicht in die Form einer Kugel dehnen und zerren.

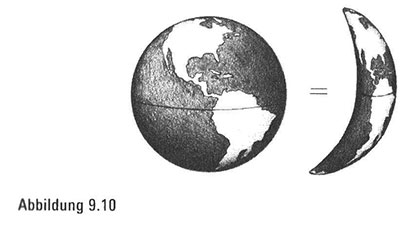
Selbst in einem Sonnensystem aus Gummifolie unterscheidet sich die Erde von einem Donut mit Zuckerguss. Wir wissen es intuitiv, aber wie können wir mathematisch beweisen, dass es selbst in einem Gummifolien-Universum unmöglich ist, einen Donut so zu dehnen und zu zerren, dass er einer Kugel ähnelt? Eigentlich haben wir alle schon einmal eine gewisse Beziehung zwischen diesen Objekten in unserem Alltagsleben erfahren: Nach dem Konsum des Ersten neigen wir dazu, dem Zweiten ähnlicher zu werden. Aber in einen Donut zu beißen und ihn zu kauen ist in dieser kalorienbewussten Studie unserer Gummigeometrie nicht gestattet. (Denken Sie daran, dass wir in der Topologie-Diät nichts entzweibrechen und zerschneiden dürfen.)

Wie wir gesehen haben, können elastische Eigenschaften zu überraschenden Ergebnissen führen, umgedrehte Kleidungsstücke inklusive. Ohne weitere Nachforschungen können wir also gar nicht sicher sein, ob es wirklich unmöglich ist, einen Donut in einen Ball umzuwandeln. Wir müssen ein Merkmal eines donutförmigen Objekts ausmachen, dass erstens im Laufe einer erlaubten Verzerrung erhalten bleibt und zweitens eine Eigenschaft ist, die der Ball nicht besitzt.
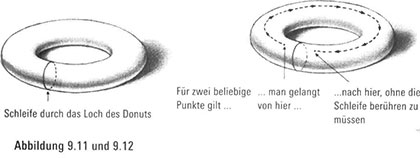
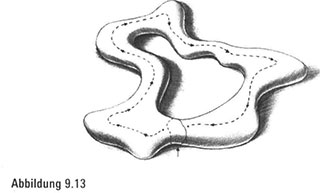
Ein Merkmal, das die erste Voraussetzung erfüllt, fällt uns auf, wenn wir einen Kreis entlang der Oberfläche eines Donuts zeichnen, und zwar so, dass der Kreis durch das Loch des Donuts führt (Abbildung 9.11). Wir stellen fest, dass dieser Kreis die Oberfläche des Donuts nicht in zwei Teile teilt. Das heißt, wir können auf der Oberfläche des Donuts von jedem beliebigen Punkt aus zu jedem anderen beliebigen Punkt reisen, ohne die Schleife berühren zu müssen (Abbildung 9.12). Müssten wir den Donut in irgendeiner Weise neu formen, ohne ihn dabei zu zerschneiden oder zu verkleben, würden wir tatsächlich erkennen, dass unsere Schleife, auch wenn sie aufgrund der Verzerrung mächtig schlangenlinienförmig aussähe, trotzdem keine zwei beliebigen Punkte auf der Oberfläche des verzerrten Donuts voneinander trennen würde (Abbildung 9.13).

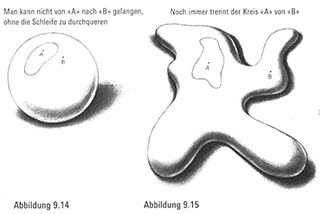
Was geschieht aber, wenn wir einen Kreis auf die Oberfläche einer Kugel zeichneten? Es stellt sich heraus, dass, ganz gleich, wie wir den Kreis auch zeichnen mögen, er die Kugeloberfläche stets in zwei Regionen teilt. Das heißt, es wird immer Punktepaare auf der Kugel geben, die durch den neu gezogenen Kreis voneinander getrennt sind (Abbildung 9.14). Diese Eigenschaft verändert sich auch nicht, wenn wir die Kugel verzerren, ohne sie dabei zu zerschneiden oder zu verkleben (Abbildung 9.14). Ganz gleich, welchen Tanz wir auch aufführen: Jede beliebige, gekrümmte Schleife wird die Kugel in zwei separate Teile trennen.

Nur um sicherzugehen, dass wir auf der richtigen Spur sind, wollen wir jetzt die Angelegenheit aus einem anderen Winkel betrachten. Nehmen wir einen Augenblick lang an, wir könnten tatsächlich den Donut in einen Ball umwandeln. Dann würde unsere kreisförmige Schleife durch das Donutloch während der Verzerrung gestreckt und gekrümmt und endete als gekrümmte Schleife auf der Kugeloberfläche (Abbildung g.16). Folglich würde die Oberfläche des Donuts aus einem Stück (ohne unseren Kreis) in zwei separate Teile auf der Kugeloberfläche verzerrt werden (Abbildung 9.17).

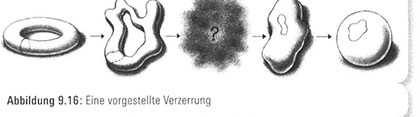
Mit anderen Worten: Durch bloßes Dehnen und Schrumpfen, aber, ohne schneiden zu müssen, sind wir in der Lage, eine Oberfläche aus einem Stück in eine zweiteilige Oberfläche zu verwandeln, was unmöglich ist: Die einzige Möglichkeit, ein einzelnes Stück in zwei Stücke aufzuteilen, ist ein Schnitt.

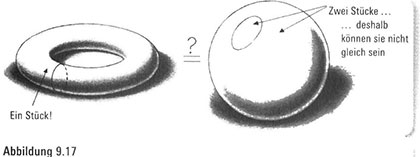
Auf diese Weise haben wir unsere Intuition bestätigt, dass selbst in einer Welt übertriebener Dehnbarkeit eine Kugel sich von einem Donut unterscheidet. Unter diesen glücklichen Umständen erkennen wir, dass mathematisches Denken unsere Intuition bestätigt hat. Wenn wir jedoch den Vorschlag machen, unseren Verstand um einen Diamantring kreisen und sich dehnen zu lassen, führt die Hochzeit zwischen Realität und unserer Intuition leider zu einer peinlichen Trennung.
Zwei Löcher) ein Ring, null Scheidungen Nehmen wir an, uns fiele eine Gummischeibe mit zwei Löchern Und einem Diamantring in die Hände, der durch diese beiden Löcher führte (Abbildung 9.18). Für unsere Intuition mag es auf der Hand liegen, dass wir die Gummischeibe nicht so dehnen und verzerren könnten, dass der Ring nur durch ein einziges Loch ginge (Abbildung 9.19).

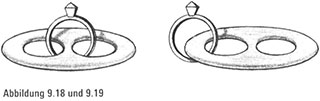
Um ein solches Ergebnis zu erzielen, müssten wir die Gummischeibe schon aufschneiden und dann wieder zusammenkleben (Abbildung 9.20) – es wäre unmöglich, den Ring aus einem der Löcher allein durch Strecken und Dehnen zu befreien.

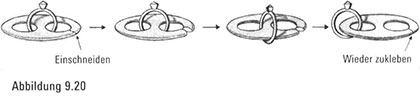
Überraschung. Solch eine vermeintlich unmögliche Aktion ist in der Tat machbar. In Erinnerung daran, dass ein Bild so viel wert ist wie tausend Worte, präsentieren wir in Abbildung 9.21 die Details dieses phantastischen topologischen Kunststücks.

Wie Sie sehen können, ist der erste Schritt einfach und direkt – wir lassen die Gummischeibe abschlaffen und dehnen eines der Löcher, sodass es etwas größer wird. Der nächste Schritt ist eine weitere leichte Streckung – wir ziehen den Rand des mittlerweile größeren Lochs über der Ring. Im nächstfolgenden Schritt wird veranschaulicht, wie wir dehnen und strecken, ohne zu schneiden. Wir wenden keine Tricks dabei an, keine Spiegel, keinen doppelten Boden. Denken Sie daran, dass wir es mit unbegrenzter Elastizität zu tun haben und es an uns selbst liegt, mit unserem Verstand gleichermaßen flexibel umzugehen.

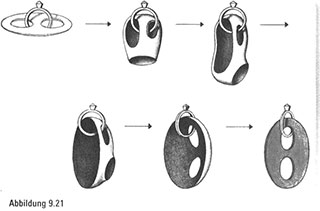
Wir fahren also fort und erkennen, dass der Ring, der anfangs eindeutig durch zwei Löcher ging, nunmehr nur noch durch ein einziges Loch geht.

Selbst nach dem Studium der Bilder bleibt ein Geheimnis ungelöst. Wie konnten wir es ohne Schnitte schaffen, den Ring aus einem Loch zu entfernen? Die Antwort lautet erstaunlicherweise, dass wir dies gar nicht getan haben, denn nach unseren vollzogenen Schritten geht der Ring noch immer durch die beiden gleichen Löcher! Wenn wir den Dehnprozess aufmerksam verfolgen, erkennen wir Folgendes: Was zu Anfang das kleine Loch auf der fechten Seite war, ist jetzt so weit gedehnt, dass es die Außenkurve der Gummischeibe darstellt, während die ursprüngliche äußere Begrenzung der Gummischeibe zum kleinen, unverbundenen Loch auf der rechten Seite geworden ist (Abbildung9.22). Der Ring ist noch immer mit beiden Löchern verbunden – wir haben lediglich eines dieser Löcher in die äußere Begrenzung umgewandelt.

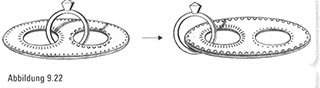
Diese Illusion der Verlagerung des Rings ist eine Herausforderung für unsere Intuition und veranschaulicht die Wunder und die seltsamen Wendungen, die in einem amorphen Universum möglich sind. Von größerer Bedeutung ist jedoch, dass die Puzzles einen Einblick in das immer wiederkehrende Thema unseres Sportwetten-Ratgebers verschaffen, nämlich wie wir denken und wie wir der Welt einen Sinn geben. Hier erkennen wir, was eine Überraschung in Wirklichkeit ist – ein Augenblick, in dem wir entdecken, dass unsere Intuition im Widerspruch zur Realität steht.

Wenn wir von einem bestimmten Ergebnis oder Ereignis überrascht werden, sollten wir wohlweislich anerkennen, dass es eine Lücke zwischen unserer Wahrnehmung und der Wirklichkeit gibt. Eine Überraschung sollte daher ein Signal sein, das uns dazu auffordert, unsere Intuition und unser Denken neu auszurichten, so- dass sie mit der Realität übereinstimmen. Eine der Lektionen, die uns das mathematische Denken lehrt, läuft darauf hinaus, dass wir eine überraschende Situation stets aus verschiedenen Perspektiven und Blickwinkeln neu untersuchen sollten, bis das Gefühl des Überrascht seins durch ein grundsolides intuitives Verständnis der Wahrheit ersetzt worden ist.

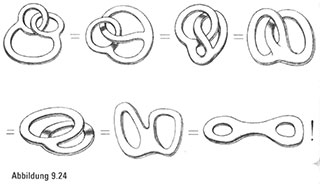
Unsere nächste Überraschung, die uns die Augen öffnen soll, dreht sich um die folgende topologische Herausforderung: Ist es möglich, einen Donut, dessen zwei Löcher miteinander verknüpft sind (Abbildung 9.23a), in einen unverbundenen, zweilöchrigen Donut (Abbildung 9.23b) zu verzerren, ohne dabei aufs Schneiden oder Kleben zurückzugreifen?

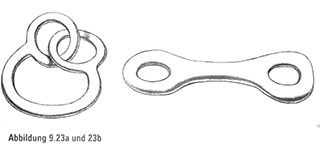
Die erhellende, unerwartete Antwort lautet… nun, sehen Sie selbst. Wir präsentieren hier eine Reihe von Bildern, die sich durch kleine und leicht ausführbare Dehnungen voneinander unterscheiden (Abbildung 9.24). Wir verzichten dabei auf einen detaillierten Kommentar.

So extravagant diese Puzzles auch erscheinen mögen, derartige topologische Konstrukte haben tatsächlich Auswirkungen auf die reale Welt. Lassen wir die Überraschungen beim Ausziehen und

Entknüpfen jetzt hinter uns, und kommen wir zum verqueren mikroskopischen Universum des Lebens an sich. Hier liegt die Überraschung darin, wie unsere ständig verdrehte Telefonschnur zu Einsichten in die geheimnisvolle Welt der DNS führen kann.

Verhedderte Schnure und verknotete DNS entwirren
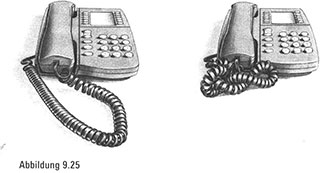
In den finsteren Zeiten vor der Erfindung des Mobiltelefons hatten wir alle Telefone, deren Schnüre sich auf mysteriöse Weise verhedderten (Abbildung 9.25). Und lange Zeit vor dem Telefon besaßen wir alle schon DNS, die sich auf geheimnisvolle Weise im Kern jeder einzelnen Zelle verknotet.

Das Schnurtelefon bescherte dem amerikanischen Telefonkonzern Mama Bell ein Kommunikationsmonopol (bis sie gezwungen war, all jene Baby-Bells zu gebären), während die DNS jedem von uns das Monopol auf unsere Individualität verleiht. Was haben diese unterschiedlichen Welten miteinander zu tun? Die Verbindung wird durch den topologischen Begriff des Knotens hergestellt.

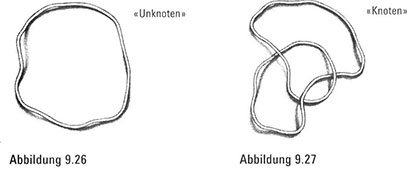
Ein mathematischer Knoten ist einfach ein geschlossener Faden als Schleife, die verknotet sein kann oder nicht. Der einfachste Knoten ist eine Schleife, die überhaupt keinen Knoten hat und Unknoten genannt wird (Abbildung 9.26). (Die Tatsache, dass die Mathematikergemeinde den Unknoten einen Knoten nennt, ist Grund Nr. 73 dafür, warum die Leute dazu neigen, sich nicht mit Mathematikern abzugeben.) Normale Menschen betrachten einen Knoten als Schleife, die wirklich verknotet ist. Was aber verstehen Mathematiker unter einer verknoteten Schleife (Abbildung 9.27)} Nun, es bedeutet, dass die Schleife nicht in einen runden Kreis – alias einen Unknoten – überführt werden kann, ohne zerschnitten zu werden.

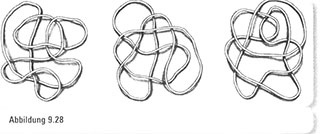
Leider ist es nicht immer leicht, festzustellen, ob ein verheddertes Knäuel wirklich verknotet ist oder nicht. Können wir denn beispielsweise nur durch Hinsehen herausfinden, welches der in Abbildung 9.28 gezeigten Knäuel in einen Unknoten entwirrt werden kann? Wir glauben nicht. Zufällig ist es der Wirrwarr in der Mitte, der in einen Unknotenkreis entweder werden kann, während die beiden Schleifen daneben nie vollständig entknotet werden können. Unsere Unfähigkeit, echte Knotenhaftigkeit auf den ersten Blick festzustellen, sollte uns jedoch nicht peinlich sein: Es ist einfach nicht möglich, sich Bilder zweier Knoten anzuschauen und festzustellen, ob einer davon so manipuliert werden kann, dass er aussieht wie der andere. Vielleicht denken Sie, es sollte möglich sein, die Muster zu studieren, die von gewebten Netzen unter- und übereinander verlaufender Schnüre erzeugt werden, um festzustellen, welches Durcheinander tatsächlich ein Knoten ist und welches nicht.

Aber bis jetzt hat noch niemand ein einfaches Verfahren entdeckt, das für jedes Knotenwirrwarr gilt. Selbstverständlich können wir, sofern es uns gestattet ist zu schummeln, immer jeden Knoten zu einem Unknoten entwirren. Dazu müssten wir dann aber verschiedene Kreuzungen verändern, indem wir die Fäden aufschneiden und wieder verkleben. Wie wir gleich entdecken werden, führt uns die Topologie – das Studium der Gummifoliengeometrie – zu der Einsicht, dass das Leben selbst nicht immer alle Regeln befolgt.

Die Würze des Lebens
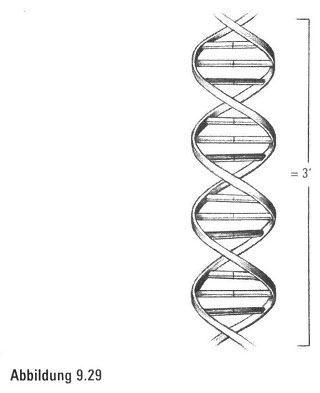
Die spiralförmige Doppelhelix (Abbildung 9.29) ist eines der berühmtesten Gebilde in der Biologie, weil sie die Struktur des Lebensmoleküls DNS (Desoxyribonukleinsäure) beschreibt. Biologen berichten, das Wesen unserer Existenz sei in diesem einen Meter langen DNS-Strang codiert, der im Kern jeder einzelnen Zelle des menschlichen Körpers zu Hause sei.

Allerdings brauchen wir kein Biologiediplom, um zu erkennen, dass der mikroskopisch kleine Zellkern unmöglich zur Speicherung eines Objekts von der Form und Länge eines Meterstabs geeignet ist. Um diesen langen DNS-Faden in den winzigen Einzimmerkern zu Stopfen, müssen wir ihn zusammendrücken. Doch wollte man die DNS komprimieren, indem man sie auf einen einzigen Punkt zusammenquetschte, erzeugte man viel zu viel potenzielle Energie tu ihrem (und zu unserem) Vorteil. Also lernt Mutter Natur ihre Lektion von Mama Bell und der Topologie der verhedderten Telefonschnüre.

Die in Abbildung 9.25 gezeigte aufgewickelte Schnur eines Schnurtelefons besitzt ein paar der geometrischen Eigenschaften der DNS. Eine der wichtigsten ist, dass sich die Schnur leicht verdreht (und sich obendrein windet) und sich folglich festzurrt. Wir entwirren nun diese problematischen Verrenkungen, indem wir den Hörer abnehmen und ihn abwickeln lassen, bis die Schnur zu ihrer normal aufgewickelten, aber nicht verhedderten Form zurückgekehrt ist. Diese einfache Übung mit Schnurtelefonen veranschaulicht die Lösung der Natur für das Speicherungsproblem der DNS. Die DNS wickelt sich wie die Telefonschnur selbst auf, was Supercoiling (mehrfache Aufspulung) genannt wird. Dadurch wird die DNS befähigt, in enge Räume zu passen (wie etwa in den Kern Ihrer Lieblingszelle), ohne überschüssige Energie aufzubauen. Wenn Ihnen das nächste Mal eine schlimm aufgewickelte Telefonschnur begegnet, seien Sie nicht so verärgert. In dieser Gestalt hat die Natur eine topologische Möglichkeit gefunden, wie sich unsere DNS in einen engen Kern hineinschmiegen kann. Und es funktioniert perfekt – bis die DNS den Drang verspürt, sich fortzupflanzen.

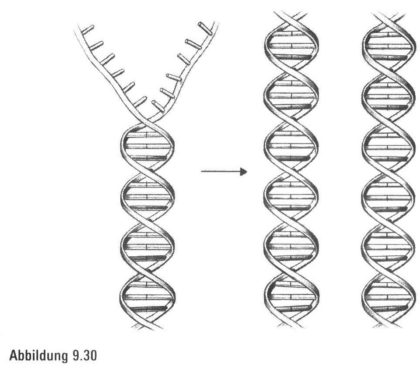
Wenn eine Zelle sich teilt, möchten sich die neuen Zellen nicht gemeinsam in die Obhut dieses einen DNS-Strangs begeben, sondern jede Zelle braucht ihre eigene DNS. Also teilt sich die DNS in zwei Stränge auf- die eine begibt sich in die eine Zelle, die zweite in die andere Zelle. Theoretisch können wir uns verstellen, wie die wunderschöne DNS-Spirale, Sprosse für Sprosse, sich langsam in der Mitte entfaltet und aufteilt (Abbildung 9.30). Die Topologie sagt uns jedoch, dies sei unmöglich. Die beiden Seiten der DNS-Leiter sind so eng umeinander aufgewickelt, und obendrein ist die DNS noch mehrfach aufgespult (Supercoiling). In dieser verknoteten Anordnung ist es unmöglich, die beiden Stränge auseinanderzuziehen, nachdem die Sprossen getrennt sind.
Wenn Sie sich selbst davon überzeugen möchten, dass die Trennung der beiden Spiralen unmöglich ist, versuchen Sie einmal, zwei ein Meter lange Bindfäden zu einer dichten Kugel zu bündeln, zu wickeln oder zu kneten. Versuchen Sie anschließend, die Fäden voneinander zu trennen, indem sie zwei Enden ergreifen und mit aller Kraft an ihnen ziehen.

Sie werden sehen, dass die Stränge sich mit Sicherheit verknoten werden. Aus diesem einfachen Experiment lässt sich schließen, dass die Vorstellung auseinandergezogener Hälften der DNS-Leiter nicht richtig sein kann. Topologische Tatsachen über verbundene Fäden erweisen sich als unwiderlegbare biologische Realität der DNS -Replikation, ohne dass wir viel Geld für Laborexperimente ausgeben müssen – dies ist eine weitere Demonstration der Macht abstrakter Mathematik.

Im Laufe des Trennungsvorgangs können die beiden Hälften der DNS-Leiter nicht heil bleiben. Die Topologie beweist, dass die Natur schummeln muss. Um mit der Verdrillung und dem Supercoiling umgehen zu können, müssen die Hälften der Leiter sich irgendwie durcheinander hindurchbewegen, um die verhedderte DNS-Kugel ein wenig zu entknoten. Und die Natur schummelt tatsächlich: Während der DNS-Replikation werden die Leiter hälften durchtrennt, bis sie nach dem Durchgang auf die andere Seite sich wieder aneinanderheften – ein absolut regelwidriger Schritt in einer topologischen Welt. Hier wird nicht mit Messern und Klebestreifen geschnitten und geklebt. Das besorgen ausgezeichnete Enzyme, die die DNS entwirren und jede Hälfte ihr eigenes Leben führen lassen.

So führt uns das Spiel mit abstrakten Vorstellungen im Rahmen eines fiktiven, amorphen Universums zu erstaunlichen Einsichten in die Starrheit unserer wirklichen Welt. Die grundlegendsten Aspekte unseres Lebens werden eindeutig von topologischen Problemen bestimmt. Nach diesem kurzen Eintauchen in den Genpool trocknen wir uns ab, verlassen den Mikrokosmos und schließen das Kapitel mit einer Reihe physikalischer Experimente ab, die unsere Neugier wecken und unsere Intuition herausfordern sollen.

Irrungen und Wirrungen in einem gestaltlosen Universum – Lotto Tipps Teil 2