Irrungen und Wirrungen in einem gestaltlosen Universum – Lotto Tipps Teil 2

Irrungen und Wirrungen in einem gestaltlosen Universum – Lotto Tipps Teil 1

Schicksalstwist
Wie oft hören wir, dass man beide Seiten der Medaille betrachten muss. Hier jedoch entdecken wir eine auf elegante Weise verdrehte Welt, in der wir zwar zwei Seiten erwarten, aber dann doch nur eine einzige vorfinden. Diese Welt, die in Wahrheit ein zu einer Schleife verdrehter Streifen ist, kennt man unter dem Namen Möbiusband oder Möbiusschleife. Es kann auf eine glänzende Karriere zurückblicken. Seine attraktiven Kurven schmücken Museen, und sogar das allgegenwärtige Recyclingsymbol ist auf das Möbiusband zurückzuführen. Bei unserem letzten Ausflug in die Topologie wollen wir jetzt unsere Intuition in Bezug auf verdrehte Welten durch ein paar einfache Experimente mit Papier und Schere auf die Probe stellen. Dabei werden wir die Bedeutung und die Raffiniertheit einer einzigen Verdrehung aufdecken.

Wir fangen mit dem Bau eines Möbiusbands an – und bitten Sie eindringlich, mitzumachen und sich selbst eines anzufertigen. Nehmen Sie einen Streifen Papier von etwa 30 Zentimeter Länge und 5 Zentimeter Breite und halten Sie die beiden Enden zusammen, um eine rundliche, zylindrische Schleife zu erzeugen (Abbildung 9.31). Beachten Sie, dass es zwei Seiten hat (eine Innenoberfläche und eine Außenoberfläche) und zwei Kanten (eine obere und eine untere).

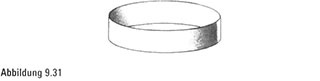
Diese Form erinnert Sie vielleicht an das Etikett einer Thunfischdose und kommt uns ziemlich normal und vertraut vor.

Aber ein Thema unseres Sportwetten-Ratgebers ist ja, wie Sie vielleicht bemerkt haben, dass das Faszinierende nur durch einen kleinen Dreh vom Banalen entfernt ist. Also machen wir jetzt buchstäblich einen Dreh. Wir drehen einfach ein Ende um und bringen damit eine Wendung – oder, um genauer zu sein, eine halbe Wendung in unseren Streifen hinein. Danach versiegeln wir die Enden mit Klebeband und schauen uns die Kreation an (Abbildung 9.32). Das vor uns liegende Objekt ist ein Möbiusband. Es ist gebündelte Eleganz, Anmut, Schönheit, Charme, Faszination und Geheimnis.

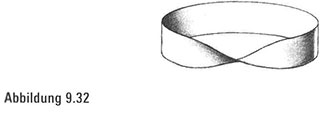
Einspuriger Geist
Wie kann eine Papierschleife all diese wunderbaren Eigenschaften verkörpern? Beginnen wir unsere Untersuchung, indem wir einen Finger in Tusche tauchen (oder einen dünnen Filzstift suchen) und dann mit ihm langsam an einem Rand des Streifens entlangfahren, sodass er die Tinte aufsaugt. Wenn wir zu unserem Ausgangspunkt zurückkehren, wundern wir uns vielleicht, dass wir alle Ränder mit Tinte markiert haben – das heißt, wir sehen keinen tintenfreien Rand mehr (.Abbildung 9.55). Dabei scheint es doch selbstverständlich zu sein, dass ein Streifen zwei Ränder hat – und unser Band sah auch in der Tat so aus, als es noch einem Thunfischdosenetikett ähnelte -, aber das Möbiusband trotzt der Vernunft und hat nur einen Rand.

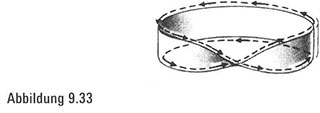
Betrachten Sie nun die Seiten der Möbiusschleife. Mit einem Stift (oder Tusche auf der Fingerspitze) beginnen wir auf der Außenseite und ziehen auf mittlerer Höhe eine Linie (Abbildung 9.34). Wenn wir schließlich zum Ausgangspunkt zurückgekehrt sind, erkennen wir ein seltsames Phänomen:

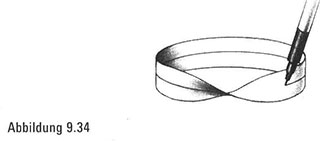
Wir haben beide Seiten überquert, ohne unseren Stift (oder, falls wir Tusche benutzen, ohne unseren Finger) anzuheben. Eigentlich haben wir damit gezeigt, dass es nur eine Seite gibt!

Folgende Methode ist eine literarische Art und Weise, diese Tatsache zu bestätigen. Wir nehmen einen Papierstreifen und schreibe auf eine Seite: Ein Möbiusstreifen hat nur eine Seite. Das habe Ich , sodass sie die ganze Länge des Streifens bedeckt. Anschließend drehen wir den Streifen um, indem wir den unteren Rand über den oberen Rand wenden, und Schreiben nun auf diese Seite den Text: Wirklich in entdeckt (und bitte verwenden Sie keinen Bindestrich). Wenn wir jetzt ein Möbiusband herstellen, indem wir den Streifen halb drehen und das rechte Ende mit dem linken verkleben, haben wir eine inspirierende wahre Geschichte geschrieben, die weder einen Anfang noch ein Ende hat, aber das ganze Möbiusband bedeckt. Diese Einheit von Rand Und Fläche ist eine überraschende Entdeckung, die, wie wir gleichеn werden, zu anderen faszinierenden Eigenschaften führt.

Den Schnitt machen
Die Möbiusschleife offenbart ihre Schönheit nicht nur oberflächlich betrachtet, denn wir finden noch weitere verborgene Reize. Angenommen, wir schneiden den Streifen mit einer Schere längs in zwei Hälften – das heißt, entlang der Mitte des Streifens -, bis wir zu unserem Ausgangspunkt zurückkehren (Abbildung 9.35). Normalerweise erhalten wir zwei Teile, wenn wir einen Gegenstand entzweischneiden. Hier aber entdecken wir, dass das Möbiusband mit der Normalität nicht viel zu tun hat.

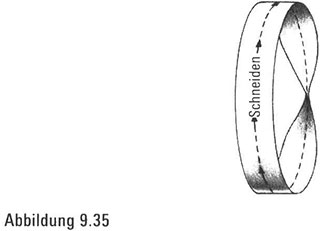
Die einzige Möglichkeit, das Experiment wirklich zu verstehen, ist der eigene Versuch. Stellen Sie ein Möbiusband her und schnei den Sie es längs genau in der Mitte auf. Das Ergebnis wird Sie überraschen: Es ist ein einziger langer Streifen, der zwei Drehungen hat. Wie können wir nun unser Verständnis für das Möbiusband so vertiefen, dass dieses faszinierende Resultat Sinn macht? Mit anderen Worten, wie können wir so vertraut mit dem verführerischen Möbiusband werden, dass dessen hervorstechende Eigenschaften, nur eine einzige Seite und eine einzige Kante zu haben sowie auch nach dem Aufschneiden nur aus einem einzigen Stück zu bestehen, •offen zutage treten?

Ein wenig Montage muss sein
Eine erfolgreiche Betrachtungsweise der Welt ist die Suche nach ihrer Konstruktionsweise. Die Konstruktion des Möbiusbands kann anhand eines Erkennungsdiagramms beschrieben werden-, das ein Objekt in seinem vormontierten Zustand darstellt. Ein Erkennungsdiagramm besteht aus einem rechteckigen Papierstreifen mit Anweisungen, die erklären, welche Kanten zusammengeklebt werden sollen, um das Objekt herzustellen. Die Montageanweisungen bestehen aus Pfeilen, die paarweise auf die Kanten gezeichnet sind. Diese Kanten müssen so zusammengeklebt werden, dass die Pfeile in dieselbe Richtung weisen.

Bevor wir uns mit dem Möbiusband beschäftigen, wollen wir uns ansehen, wie wir das Erkennungsdiagramm für ein einfacheres Objekt (Abbildung 9.36) zeichnen würden.

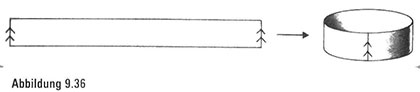
Wenn wir Pfeile auf die eine Kante zeichnen und auf die andere Kante Pfeile, die in die gleiche Richtung zeigen, und diese Kanten dann so zusammenkleben, dass die Pfeile in einer Linie ausgerichtet sind, haben wir einen rundlichen Zylinder hergestellt, der an unser Thunfischdosenetikett erinnert. Wie erzeugen wir nun das entsprechende Erkennungsdiagramm für die Möbiusschleife?

Es läuft darauf hinaus, dass die Pfeile an den Kanten in entgegengesetzte Richtungen zeigen müssen (Abbildung 9.37).

Bringen wir nun die Kanten mit einer halben Drehung zusammen, dann haben wir ein Möbiusband konstruiert. Zu diesem Zeitpunkt aber wollen wir diesen letzten Schritt noch nicht tun. Stattdessen untersuchen wir einfach den freien, nicht verklebten Papierstreifen, nämlich unsere nicht montierte Möbiusschleife. Angesichts der durch die Pfeile angedeuteten Klebeanweisungen erkennen wir nun: Sobald wir uns von einem Punkt aus auf die rechte Kante zubewegen, schießen wir an dem damit verbundenen Punkt auf der linken Seite wieder hervor (Abbildung 9.38). In gewissem Sinne reisen wir auf einem verdrehten PacMan-Bildschirm ostwärts. Liefe demnach ein PacMöbiusMan sein nicht fertig montiertes Möbiusband entlang in Richtung obere Kante rechts, tauchte er im selben Moment auf der unteren linken Kante wieder auf (Abbildung 9.49).

Das Erkennungsdiagramm befähigt uns, die Merkmale des Möbiusbands leichter zu erkennen. Bewegen wir uns beispielsweise am oberen Rand entlang ostwärts fort, gelangen wir schließlich zur oberen rechten Ecke. Wenn die Kanten des Möbiusbands zusammengeklebt sind, ist diese Ecke mit der unteren linken Ecke verbunden.

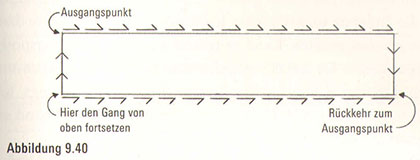
Während wir also fortschreiten, sehen wir, dass der untere Rand des nicht montierten Bands in Wirklichkeit nur eine Fortsetzung des oberen Rands ist. Wenn wir nun zu der unteren rechten Ecke kommen, wird sie an der oberen linken Ecke befestigt sein, sodass wir uns von dort aus zurück zum Ausgangspunkt begeben können, nachdem wir sowohl den oberen als auch den unteren Rand des Papierstreifens überquert haben (Abbildung 9.40). Folglich haben wir geometrisch bewiesen, dass es nur einen Rand des Möbiusbands gibt, so wie wir es zuvor bereits mit unserem Tutschefinger festgestellt haben.

Eine schneidige Persönlichkeit
Das Erkennungsdiagramm zeigt auch, warum nur ein Stück übrig bleibt, nachdem wir die Möbiusschleife entlang der Mitte aufgeschnitten haben (Abbildung 9.41). Um dieses Phänomen nachzuvollziehen, bitten wir einfach eine Ameise, sich in östlicher Richtung entlang der nicht montierten oberen Hälfte fortzubewegen, des nicht montierten Bands gelandet. Sie setzt ihren Weg fort, bis sie an die äußerste untere rechte Kante gerät, von wo aus sie dann auf den oberen rechten Rand tritt und zu ihrer Ausgangsposition zurückkehrt. Da unsere Ameise sowohl auf den oberen und unteren Hälften des aufgeschnittenen Streifens unterwegs war, bestätigte sie, dass ein in Hälften zerschnittenes Möbiusband ein einziges Stück bleibt.

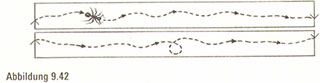
Um Ihre Phantasie anzuregen und weiterhin Ihre Intuition über das Möbiusband zu provozieren, stellen wir die folgende Frage: Was geschähe, wenn wir das Band längs durchschneiden würden, nur dass wir dieses Mal, statt direkt an der Mitte entlangzuschneiden, beim Schneiden einen festgelegten Abstand von, sagen wir, 0,5 Zentimetern zum Rand einhalten (Abbildung 9.44). Dieses Experiment ist wirklich großartig. Wenn Sie es ausprobieren, geben Sie bitte nicht der großen Versuchung nach, von der Route dicht an Rand abzuweichen – zwingen Sie sich, auf Kurs zu bleiben, und überschreiten Sie nie die imaginäre Mittellinie! Und vermeiden Sie es auch, einen Blick auf die Fußnote zu werfen, in der das Ergebnis dieses Schnittkunststücks enthüllt wird.

Abbildung 9.43: Mit der Schere am linken Rand bleiben

Sobald wir das Experiment beendet haben, werden wir bei der Betrachtung des Schnitts auf dem Erkennungsdiagramm feststellen können, warum das überraschende Ergebnis eigentlich gar nicht so verblüffend ist (Abbildung 9.44).

Sind wir uns erst einmal der Möbiusschleife bewusst geworden, sehen wir sie plötzlich überall. Wir finden sie in der Tat am unteren Rand fast jeder Plastik- oder Glasflasche oder auf Kartons, die recycelbar sind (Abbildung 9.45). So ist das Möbiusband nicht nur an sich faszinierend, sondern es hat auch mit Umweltbewusstsein zu tun.

Ausgerollte Donuts
Eine weitere wichtige Lektion, die uns mathematisches Denken im Alltag bietet, ist ein Verfahren zur Erzeugung neuer Ideen und zur Steigerung der Kreativität. Für diese Methode müssen wir einfach nur das Bedürfnis nach einem Thema haben und über Variationen dieses Themas nachdenken. So schufen wir beispielsweise in diesem Kontext ein Erkennungsdiagramm für das Möbiusband, mit Anweisungen für die Befestigung der beiden kurzen Seiten eines Rechtecks. Mit dem Möbiusband als Inspiration im Hinterkopf können wir jetzt unterschiedliche Seitenerkennungen für einen Bogen Papier betrachten und dadurch neue und exotische Oberflächen entdecken und erzeugen.

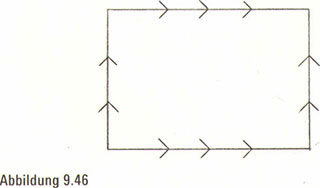
Nehmen wir beispielsweise an, wir bestimmten die beiden Paare der gegenüberliegenden Seiten eines Rechtecks (zwei horizontale und zwei vertikale Seiten) und zeichneten Pfeile, die für jedes Paar in die gleiche Richtung zeigten (Abbildung 9.46). Wenn wir nun das rechteckige Blatt Papier so krümmten, dass die oberen und die unteren Pfeile in einer Linie ausgerichtet wären, und dann die beiden Ränder zusammenklebten, hätten wir einen Zylinder geschaffen. Beachten Sie, dass dieser Zylinder zwei kreisförmige Ränder hat, die mit Pfeilen markiert sind.

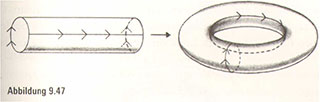
Biegen wir nun den Zylinder so, dass die Pfeile auf den kreisförmigen Rändern übereinstimmen, haben wir die köstliche Oberfläche eines Donuts geschaffen (Abbildung 9-47).

Eine Flasche mit dem gewissen Dreh
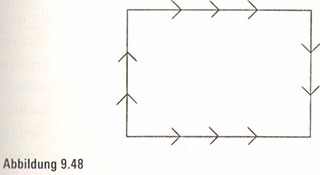
Warum sollten wir jetzt nicht versuchen, da wir am Erfolg geschnuppert haben, die Ränder eines Rechtecks auf andere Art und Weise zusammenzukleben? Dieses Mal werden wir ein noch faszinierenderes Objekt herstellen, das die verdrehte Turbulenz des Möbiusbands mit der röhrenförmigen Gelassenheit des Donuts verbindet. Zu Beginn wollen wir einfach nur das Erkennungsdiagramm für den Donut verändern, indem wir die Richtung der Pfeile auf einer der beiden Seiten umdrehen (Abbildung 9.48), wie wir es bereits getan haben, um das Thunfischdosenetikett in ein Möbiusband zu verwandeln. Jetzt müssen wir kleben.

Wenn wir den oberen Rand mit dem unteren Rand verkleben, entsteht immer noch ein Zylinder. Bringen wir jedoch die beiden kreisförmigen Enden des Zylinders zusammen, gibt es ein böses Erwachen: Die Pfeile an diesen beiden Enden sind nicht in einer Linie ausgerichtet (Abbildung 9.49). Das eine Pfeilpaar zeigt entlang seines kreisförmigen Endes in die eine Richtung, während das andere Paar an seinem Ende in die entgegengesetzte Richtung weist. Wie können wir also die Pfeile in Übereinstimmung bringen und unsere Klebeaktion so abschließen?

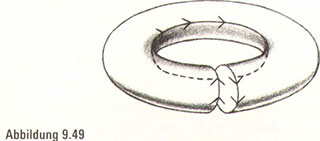
Während wir noch frustriert dasitzen und das eine Zylinderende in unserer rechten und das andere Ende in unserer linken Hand halten, stellen wir plötzlich fest, dass jetzt, da die Enden des Zylinders Seite an Seite zur Zimmerdecke zeigen, alle Pfeile in die gleiche Richtung weisen (Abbildung 4.40). Wenn wir aber unsere Hände aufeinander zubewegen, damit die Enden sich berühren, scheint es, als drehe sich das eine Pfeilpaar um – das heißt, die Pfeile zeigen in dem Augenblick nicht mehr in dieselbe Richtung, wenn die Enden sich berühren. Wir versuchen es erneut. So lange die Enden des Zylinders zur Decke weisen, zeigen die Pfeile in dieselbe Richtung, doch sobald sie sich gegenüberstehen, ist ein Pfeilpaar falsch ausgerichtet.

Wie könnte es uns gelingen, die beiden Enden zusammenzuführen, ohne dass wir ein Pfeilpaar dabei unbeabsichtigt umdrehen?

Die Antwort lautet: durch Schummeln. Wir schneiden ein Loch in die linke Seitenwand des Zylinders, und während wir unser Objekt senkrecht in die Höhe halten, fügen wir das Ende, das wir m unserer rechten Hand halten, in das Loch ein (Abbildung 9.51).

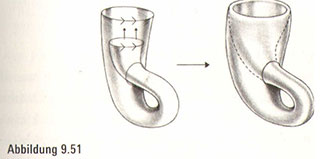
Nun drücken wir das eingefügte Teil nach oben, bis es das Ende der anderen Zylinderhälfte erreicht hat. Dort, wo die Kanten sich berühren, zeigen die Pfeile jetzt in die gleiche Richtung, sodass wir sie, wie angegeben, verkleben können. Positiv betrachtet, haben w i r gerade ein Objekt konstruiert, das als Klein’sche Flasche bekannt ist. Andererseits müssen wir zugeben, dass es eigentlich eine Klein’sche Flasche mit einem Loch ist, da wir uns ja Zugang ins Innere des Zylinders verschaffen mussten. Aber zurück zur positiven Betrachtung: Unserer Vorstellungskraft, es mit einer Klein’schen Flasche ohne Loch zu tun zu haben und über deren Eigenschaften nachzudenken, steht nichts im Wege.

Natürlich hat eine verschlossene Flasche Champagner ein Inneres und ein Außeres, doch es stellt sich heraus, dass die Klein’sche Flasche zwar auch eine geschlossene Flasche ist, aber weder ein Inneres noch ein Außeres hat. Klein’sche Flaschen haben zwei kleine Fehler – erstens würde Champagner in einer solchen Flasche sofort nicht mehr perlen, und zweitens ist eine Klein’sche Flasche ein abstraktes Objekt, das wir in unserer beschränkten Wirklichkeit nicht vollständig konstruieren können. Doch abgesehen von solchen kleinen Mängeln, sind Klein’sche Flaschen das Nonplusultra faszinierender mathematischer Formen.

Partei ergreifen für die Klein’sche Flasche und die Entfaltung unseres Universums
Die Klein’sche Flasche ist ziemlich elegant. Nun wollen wir ihr Inneres und ihr Äußeres untersuchen, indem wir unsere Ameise auf die Außenseite der Flasche setzen und sie zu einem kleinen Ausflug ermuntern (Abbildung 9.52). Da wir uns dazu entschlossen haben, die Region zu bereisen, die in gewisser Weise an die Niagarafälle erinnert (A), bewegt sie sich nach unten fort. Während ihrer Reise durch einen zylinderförmigen Korridor (B) beschleicht sie allmählich ein klaustrophobisches Gefühl; anschließend stößt sie einen Seufzer der Erleichterung aus, weil sich der Korridor erweitert (C). Wenn sie die Decke (D) erreicht, stellen wir plötzlich fest, dass sie sich nun direkt gegenüber ihrem Ausgangspunkt befindet. Folglich haben wir es hier mit dem ungewöhnlichen Umstand einer geschlossenen Flasche zu tun, die nur eine Seite hat.

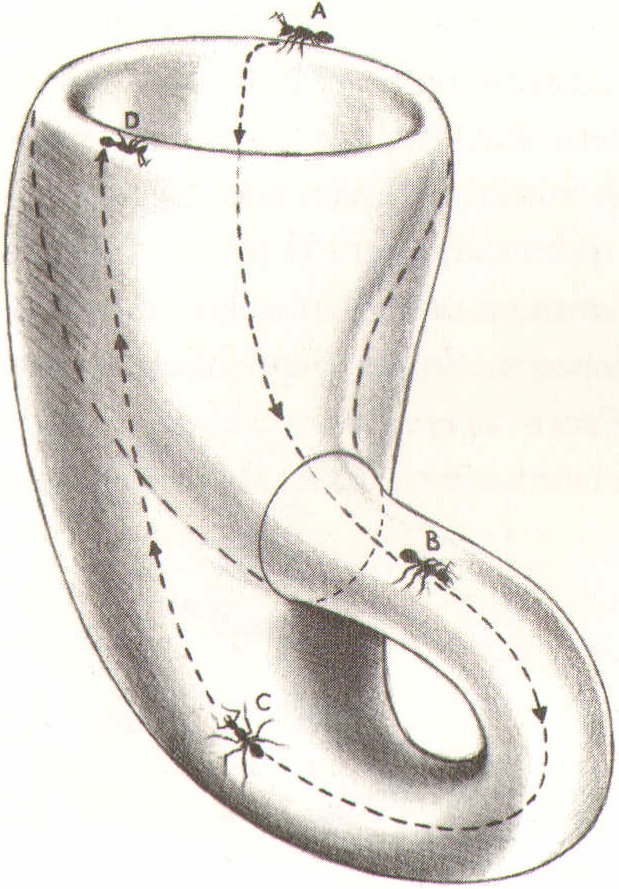
Abbildung 9.52

Die Einseitigkeit der Klein’schen Flasche sollte uns eigentlich nicht verblüffen, da wir aus dem Erkennungsdiagramm wissen, dass sie das einseitige Möbiusband enthält.

Die Klein’sche Flasche, das Möbiusband und die Donut-Oberfläche sind außergewöhnlich schöne mathematische Objekte. Diese topologischen Schöpfungen scheinen ziemlich unrealistisch und abstrakt zu sein (vom Donut einmal abgesehen!), aber sie sind ganz und gar nicht nutzlos. Wir können nämlich das Verfahren, mit dem wir diese Spielzeuge des Geistes konstruieren, auf die gewaltige Aufgabe anwenden, uns die mögliche globale Struktur des Universums vorzustellen. Die Strategie besteht darin, höher- dimensionale Entsprechungen der Erkennungsdiagramme zur Erzeugung von Klein’schen Flaschen und Donuts zu benutzen, um Modelle des Universums zu kreieren. Und so funktioniert es:

Statt mit einem Rechteck anzufangen, wie es für die Konstruktion der Klein’schen Flasche oder für den Donut erforderlich war, fangen wir jetzt mit einem Würfel an. Ein Würfel hat sechs Flächen. Angenommen, wir definieren gegenüberliegende Seiten als Paare, ähnlich wie wir die gegenüberliegenden Ränder eines Rechtecks als Paare ausgewiesen haben, um die Konstruktion eines Donuts zu beschreiben. Es ist also durchaus vorstellbar, diese drei Paare gegenüberliegender Würfelflächen zusammenzukleben. Stünde uns ein äußerst elastischer Gummiwürfel zur Verfügung, könnten wir ihn dehnen, die rechten und linken Seiten zusammenkleben und somit einen quadratähnlichen Gummidonut erzeugen (Abbildung 9.53).

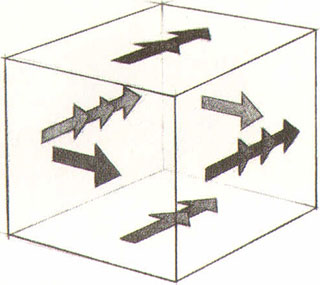
Abbildung 9.53: Die Verallgemeinerung der Oberfläche eines Donuts durch das Zusammenkleben gegenüberliegender Seiten eines Würfels

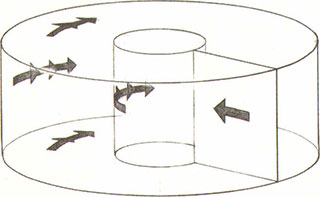
Abbildung 9.53: Ein zusammengeklebtes Seitenpaar – das Verkleben der anderen Seiten ist eine große Herausforderung.

Leider lassen sich die verbleibenden beiden vorgeschriebenen Klebeaktionen in der Realität nicht durchführen. Stattdessen sollten wir lieber das Objekt betrachten, das wir erzeugen würden, wenn uns alle drei Verklebungen gelängen.

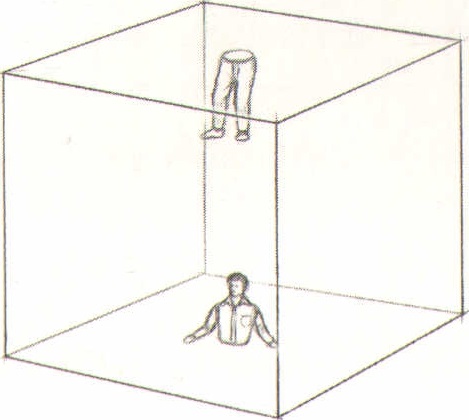
Abbildung 9.54: Ein anfangs noch verstörender Anblick, bis wir erkennen, dass die Decke auch der Fußboden ist.

Gingen wir durch eine Würfelseite hindurch, kämen wir auf der gegenüberliegenden Seite wieder heraus – wir lebten demnach in einer dreidimensionalen PacMan-Welt. Schwebten wir durch die Decke, tauchten wir am Boden wieder auf (Abbildung9.54). Schauten wir durch eine Wand, sähen wir unseren Hinterkopf. Tatsächlich sähen wir unendlich viele Exemplare von uns selbst, die in der Ferne verblassen (Abbildung 9.55).

Astronomen fragen sich, ob dieses Phänomen nicht tatsächlich am wirklichen Nachthimmel zu sehen ist. Sehen wir womöglich denselben Stern oder dieselbe Galaxie in zwei gegenüberliegenden Richtungen? Der Würfel mit erkannten Seiten ist nur ein mögliches Modell unseres Universums. Würden wir Erkennungen mit Drehungen angeben, könnten wir Modelle der dreidimensionalen Welt erzeugen, die Eigenschaften haben, die denen der Klein’schen Flasche ähnelten. Vielleicht sind wir in Wirklichkeit selbst Ameisen, die unwissentlich durch ein Klein’sches Flaschenuniversum flanieren.

Abbildung 9.55: Ein Donut-Universum. Ein Lebkuchenmännchen würde nach vorn schauen und seinen eigenen Hinterkopf sehen. Die Räume wirken endlos und unendlich, in Wirklichkeit aber haben wir es nur mit einem Würfel zu tun. Ist unser eigenes Universum wirklich endlos?

Den Platten flicken durch Reisevorbereitungen
Während unsere Entdeckung der Klein’schen Flasche uns von innen erwärmt (oder ist es doch unser Außeres?), plagt uns ein Problem. Um wirklich diese einseitige Oberfläche zu erzeugen, mussten wir den Zylinder perforieren. Lässt sich dieses Piercing vermeiden? Die Antwort lautet leider nein – die Wirklichkeit lässt das nicht zu. Aber was wäre, wenn wir nicht mehr an die dreidimensionale geometrische Wirklichkeit gebunden wären? Dann lautet die Antwort ja – wir können den Einstich vermeiden. Im nächsten Kapitel erforschen wir eine Welt, die unsere eigene Welt transzendiert. Wir werden in die vierte Dimension reisen. Dieser geräumige Spielplatz in unserer Vorstellung wird uns eine endlose Reihe faszinierender Überraschungen und eine neue Perspektive unseren Alltag bescheren. Sogar eine nicht perforierte, perfekte Klein’sche Flasche wird dort möglich sein. Wir verlassen jetzt die gestaltlose Welt der Gummifoliengeometrie mit dem Eindruck, dass das dehnbare Reich der Topologie unseren Intellekt befreit, um uns selbst und unsere Welt aus unterschiedlichen Gesichtspunkten und mit mehr Flexibilität zu betrachten.