Die Magie der vierten Dimension – Lotto und Glücksspiele Tipps Teil 2

Die Magie der vierten Dimension – Lotto und Glücksspiele Tipps Teil 1

Diese Technik lässt sich auch anwenden, um ein Problem aus unserem Sportwetten-Portal zu lösen, bei dem es um die durchbohrte Klein’sche Masche geht. Vielleicht erinnern Sie sich, dass wir zur Montage dieser wunderschönen, einseitigen, geschlossenen, flaschenähnlichen Oberfläche gezwungen waren, ein Loch hineinzuschneiden, sodass sie durch sich selbst hindurchpasste (Abbildung 10.29).

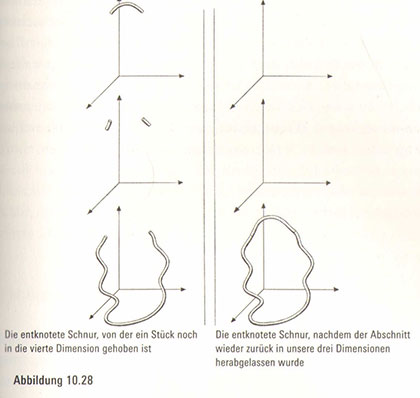
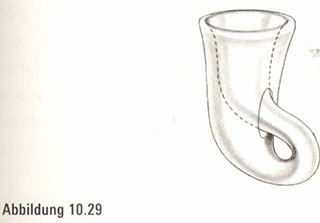
Nehmen wir nun aber die vierte Dimension in Anspruch, ist diese Schönheitsoperation an der Klein’schen Flasche nicht mehr nötig. Wir heben lediglich einen Teil ihrer Seite in die vierte Dimension (Abbildung 10.30). Während es also so aussieht, als befände sich an

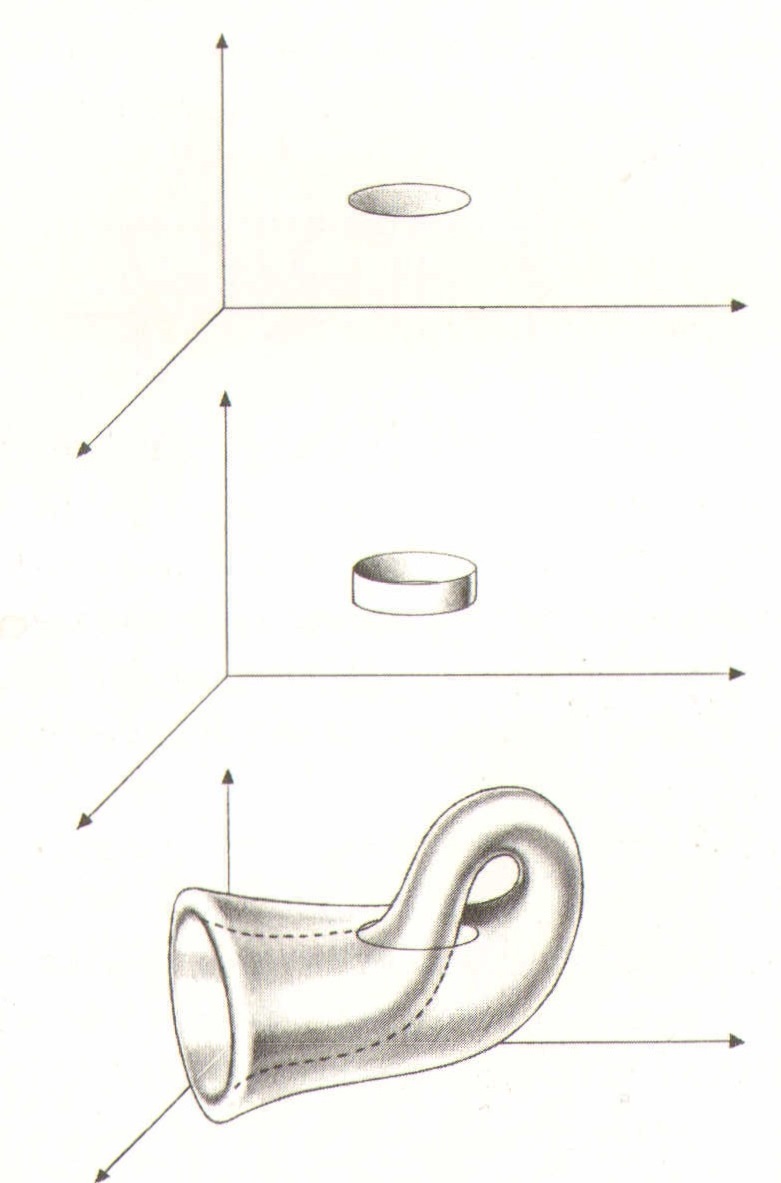
Abbildung 10.30: Eine Klein’sche Flasche kann sich in der vierten Dimension befinden, ohne dass man sie aufschneiden müsste der Außenseite des Zylinders eine Lücke, wissen wir in Wirklichkeit natürlich, dass kein Schnitt erfolgt ist – dieses nicht vorhandene Stück schwebt in der vierten Dimension. Jetzt können wir den Zylinder durch sich selbst hindurchführen, ohne dafür ein Loch machen zu müssen – genauso wie wir die Schleife entknotet haben, ohne die Schnur zu durchschneiden.

Eine perfekte Klein’sche Flasche ohne Loch lässt sich im dreidimensionalen Raum nicht anfertigen, weil es dort nicht genügend Freiheitsgrade gibt, um die Enden des Zylinders ohne eine Durchbohrung zu verbinden. Folglich haben wir entdeckt, dass die Klein’sche Flasche ein Objekt ist, dessen eigentliches Zuhause die vierte Dimension ist.

Mit Ausziehtusche Würfel erzeugen
Ausgerüstet mit der Grundidee, aus kleineren Dimensionen höhere aufzubauen, sind wir nun in der Lage, fast jedes Dimensionsproblem anzugehen, das nur irgendwie auftauchen könnte. Um unsere multidimensionalen Fähigkeiten zu demonstrieren, werden wir einen kurzen Abstecher in die Geometrie der vierten Dimension machen und entdecken, wie man einen vierdimensionalen Würfel erzeugt.

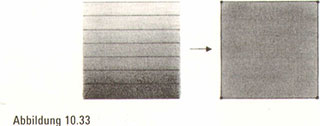
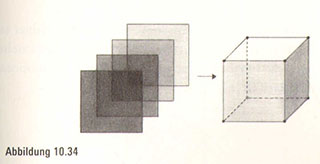
Wo sollen wir anfangen? Im Kampf mit der vierten Dimension fangen wir immer am Nullpunkt an. Was ist ein nulldimensionaler Würfel? Eine leichte Frage! In der Dimension null ist alles einfach nur ein Punkt, sodass ein nulldimensionaler Würfel ein Punkt ist, alias ein Klecks Ausziehtusche (Abbildung 10.31). Wie kommen wir von hier aus zu einem eindimensionalen Würfel? Wir ziehen den Tuscheklecks aus und verschieben ihn um eine Einheit in eine neue Richtung. Dadurch erhalten wir einen eindimensionalen Würfel, alias einen Linienabschnitt. Wenn wir diesen Linienabschnitt mit Tusche verstärken und ihn um eine Einheit senkrecht nach oben verschieben, haben wir einen zweidimensionalen Würfel oder ein Quadrat ausgetuscht (Abbildung 10.33). Nun füllen wir das ganze Quadrat (sowohl sein Inneres als auch seine Umrandung) mit Tusche aus und ziehen es um eine Einheit senkrecht zu den anderen aus, um einen dreidimensionalen Würfel, alias einen Würfel zu bekommen (Abbildung 10.34).

Wir erkennen jetzt, was wir als Nächstes tun müssen. Wir tuschen den ganzen Würfel aus – selbst die Punkte innerhalb des Würfels, als wäre der Würfel ein Schwamm – und ziehen den gesamten Würfel um eine Einheit in eine senkrecht zu allen anderen stehende Richtung.

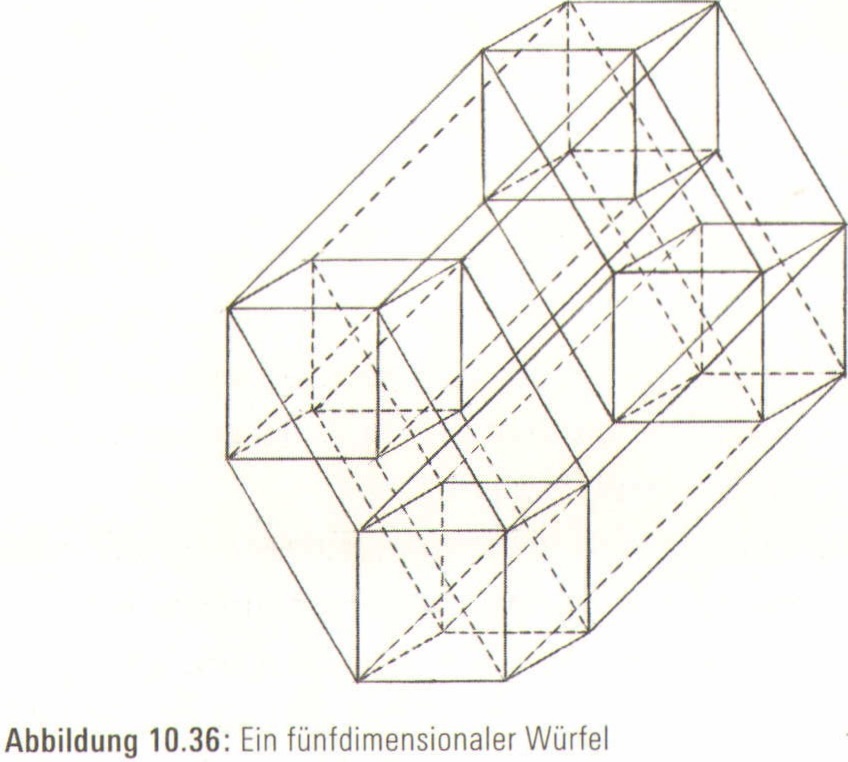
Dadurch haben wir einen vierdimensionalen Würfel geschaffen alias, nun ja, einen vierdimensionalen Würfel (Abbildung 10.35). Natürlich muss man hier nicht aufhören. Solange wir noch genügend Tinte haben, in die wir unseren Finger tauchen können, sowie neue Richtungen, in die wir die Würfel ziehen können, lassen sich Würfel von zunehmend höheren Dimensionen erzeugen (Abbildung 10.36).

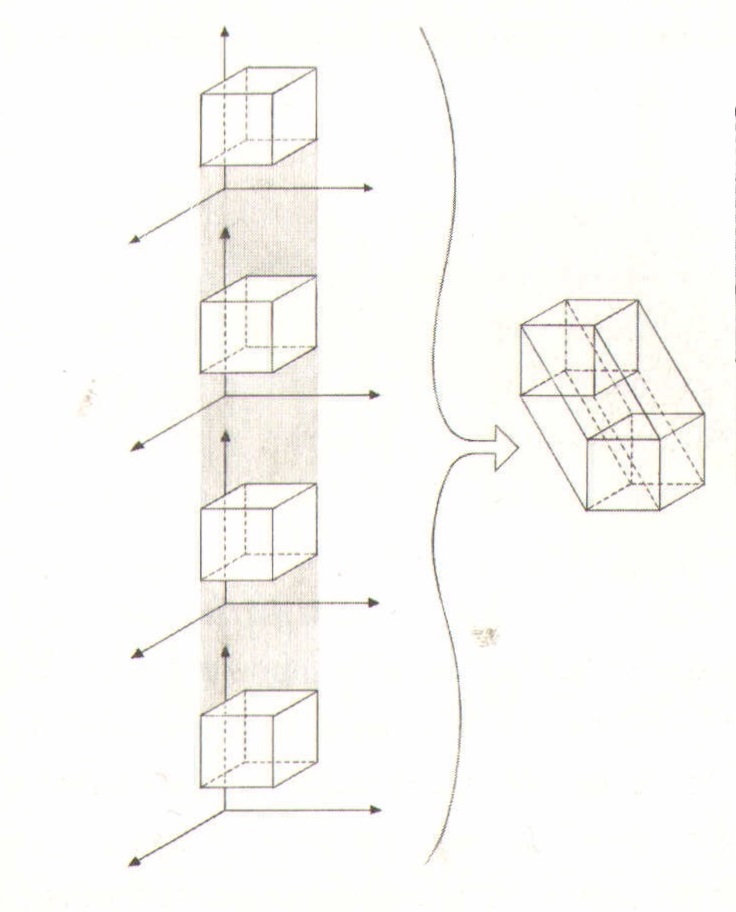
Abbildung 10.35: Zieht man einen dreidimensionalen Würfel in eine neue Dimension, gelangt man zu einem vierdimensionalen Würfel.

Den Würfel rückgängig machen
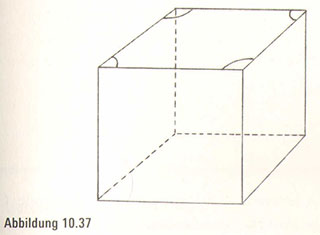
Unsere Zeichnungen drei- und vierdimensionaler Würfel leiden an der Verzerrung. Beim dreidimensionalen Würfel bilden die Seiten keine perfekten Quadrate, und nicht alle Winkel sind rechte Winkel (Abbildung 10.37). Wo liegt das Problem? Die Antwort lautet, dass wir kein genaues Ebenbild eines Würfels auf ein Blatt Papier bringen können. Der Würfel verlangt drei Dimensionen, während das Papier nur zwei anbieten kann. Mit perspektivischem Zeichnen gelingen uns die Darstellung der Winkel und der Seiten des Würfels und die Andeutung der zusätzlichen Dimension. Wenn wir die Zeichnung mit unseren dreidimensionalen Augen
betrachten, nehmen wir instinktiv diese dritte Dimension wahr; wir setzen die Einzelteile in unserem Gehirn zusammen und sehen den Würfel so, wie er aussehen soll.

Sich den vierdimensionalen Würfel vorzustellen ist schon eine größere Herausforderung, da wir keine vierdimensionalen Augen haben, um diese komplizierte perspektivische Aufnahme zu analysieren. Und beachten Sie, dass ein dreidimensionaler Würfel nur eine Dimension mehr hat als diese Seite, sodass wir bei dieser Umsetzung nur eine Dimension ausgleichen müssen. Ein vierdimensionaler Würfel hat aber zwei zusätzliche Dimensionen, weshalb wir in unserer Zeichnung eine größere Verdichtung der Dimensionen erreichen müssen. Eine genauere Wiedergabe eines vierdimensionalen Würfels könnte über ein dreidimensionales Bild erzielt werden. Obwohl es nicht möglich ist, ein dreidimensionales Modell auf einer zweidimensionalen Seite wiederzugeben, gibt Abbildung 10.38 einen Eindruck davon, wie die vier Dimensionen als dreidimensionales Abbild wiedergegeben werden könnten. In dem Modell sind die Seiten nicht rechtwinklig und treffen auch nicht in den richtigen Winkeln aufeinander.

Wir können Modelle der Grenzen drei- und vierdimensionaler Würfel erzeugen, deren Seiten perfekte Quadrate und deren Winkel korrekt sind.

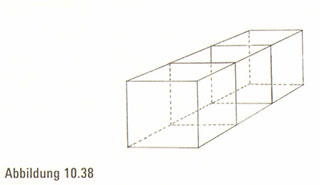
Wir erfassen sie mit einer anderen Methode. Gemäß einer Lektion der Postmoderne dekonstruieren wir die Würfel. Wenn wir die Umrisse eines dreidimensionalen Würfels entfalten, erzeugen wir sechs perfekte Quadrate, die alle rechtwinklig sind und zusammengefügt ein Kreuz bilden (Abbildung 10.39). Um den Würfel zusammenzusetzen, müssen wir die Kanten der Quadrate paarweise miteinander verbinden (Abbildung 10.40).

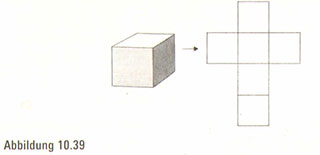
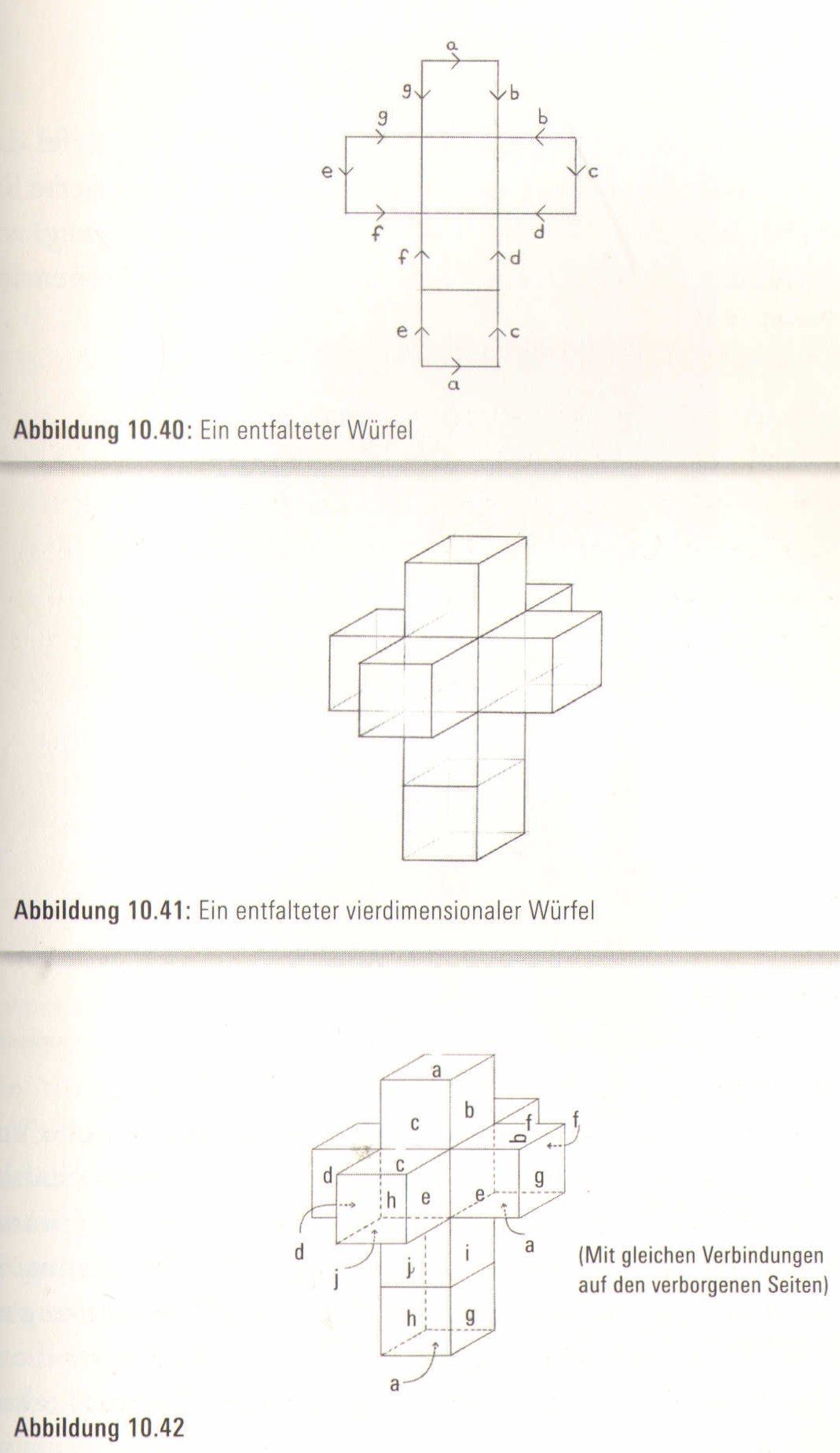
Wenn wir auf ähnliche Weise die Grenze eines vierdimensionalen Würfels entfalten, dann entdecken wir eine Menge von acht perfekten Würfeln, die alle rechte Winkel haben und so miteinander verbunden sind, dass sie ein Kreuz mit zwei zusätzlichen Armen bilden (Abbildung 10.41). Die Seiten des Würfels lassen sich zusammenkleben, sodass diese Kollektion dreidimensionaler Würfel zustande kommt, die zusammen einen vierdimensionalen Würfel ergeben (Abbildung 10.42).

Die auf Leinwand eingefangene vierte Dimension
Das faszinierende Konzept, einen vierdimensionalen Würfel darzustellen, indem man seine entfaltete Grenze zeigt, inspirierte Salvador Dali zu seinem Gemälde Corpus Hypercubus (.Kreuzigung) von 1954 (Abbildung 10.43). Darin sehen wir, wie die vierte Dimension religiöse Bedeutung annimmt.

Abbildung 10.43

Die Geometrie und die bloße Vorstellung der vierten Dimension haben Künstler, Wissenschaftler und Mathematiker gleichermaßen fasziniert. Außer Dali waren die Maler Marcel Duchamp und Max Weber dafür bekannt, in ihren Werken ausdrücklich die vierte Dimension zur Geltung zu bringen.

In Duchamps Akt, eine Treppe herabsteigend, Nr. 2 (1912) erkennen wir auf einen Blick die gesamte Bewegungsspanne, so als sei Nackte selbst mit Tinte ausgefüllt und die Stufen herabgezogen worden (Abbildung 10.44).

Abbildung 10.44

Auf diese Weise schuf Duchamp ein wundervolles Bild, das die Gesamtheit der Bewegung mit einer vierdimensionalen Metapher einfängt. Sein Werk führt uns zu der krage, ob man die vierte Dimension als Zeit verstehen kann. Sötern es uns beliebt, ja. Tatsächlich können wir diesen zusätzlichen kreiheitsgrad unterschiedlich interpretieren, auch als Klang oder karbe. Doch wenn die Zeit als Modell für die vierte Dimension gelten soll, taucht die Schwierigkeit auf, dass es uns nicht gelingt, uns so einfach vor- und zurückzubewegen wie in den anderen drei Dimensionen. Und warum sollte ausgerechnet die vierte Dimension so radikal anders sein als die anderen drei? Betrachten wir die vierte Dimension als räumlich, können wir Einsichten in eine potenzielle Geometrie und Realität gewinnen, die sich jenseits unserer vertrauten Wirklichkeit befindet.

Max Webers Das Innere der vierten Dimension (1913) stellt die vierte Dimension als unheimliche, fremdartige Welt dar (.Abbildung 10.45). Bestimmt haben wir selbst schon erkannt, wie seltsam dieser zusätzliche Freiheitsgrad ist. Vielleicht aber können wir jetzt mit Hilfe eines Vergleichs verstehen, dass die vierte Dimension eine Welt ist, die sich jenseits unseres sichtbaren Horizonts erstreckt. Wie unsere Reise und die Werke dieser Künstler bestätigen können, ist die vierte Dimension mit Sicherheit eine Quelle der Kreativität, der Schönheit und der Wunder.

Die Lektionen der vierten Dimension
Die vierte Dimension hat eine romantische, beinahe mystische Anziehungskraft. Sie scheint im Bereich der Science-Fiction zu liegen, in einer Welt, die unseren Sinnen nicht zugänglich ist. Wir haben in diesem Kapitel nicht nur versucht, uns auf die vierte Dimension zuzubewegen, sondern auch, sie anzunehmen und zu erforschen. W ir haben uns auf die Reise in die vierte Dimension gemacht und dabei recht schnell bemerkt, dass wir bei der Konfrontation mit einem schwierigen Thema die Herausforderung am besten nicht frontal in Angriff nehmen, sondern mit einem leichteren Ziel beginnen. Bevor wir uns also der vierten Dimension näherten, kehrten wir zu unserer vertrauten dreidimensionalen Welt zurück und gingen dann mit der Betrachtung der zweidimensionalen Welt noch einen Schritt weiter zurück und fragten uns, wie unser Leben wohl aussähe, wenn es in einem Universum stattfände, das aus der Oberfläche einer Tischplatte besteht.

Die Entwicklung von Ideen durch systematische Vergleiche ist eine phantastische Methode, um neue Einsichten zu gewinnen. Diese Techniken führen uns vor Augen, dass es mit unserem Verständnis selbst banaler Angelegenheiten nicht so weit her ist, wie wir manchmal glauben. Wenn wir unsere vertraute Welt aus verschiedenen Perspektiven betrachten, kann das für uns gewinnbringend und überraschend sein. Und die Schlussfolgerungen aus diesen neuen Einsichten führen manchmal zu wichtigen, bahnbrechenden Ideen. Das Ringen mit der vierten Dimension lehrt uns, die ausgetretenen Pfade des Denkens zu verlassen, was uns zu einer gänzlich neuen Dimension jenseits unserer Alltagserfahrung führt. Jetzt nähert sich unsere Reise ihrem Ende. Zum Schluss wollen wir die endlichen Dimensionen verlassen und uns in das endlose Universum der Unendlichkeit begeben.