Die Magie der vierten Dimension – Lotto und Glücksspiele Tipps Teil 1

glaub mir: Nebenan, da gibt’s ein tolles Universum. Gehen wir hin.
E. E. Cummings

Offensichtlich … Die Spannung steigt, während ein Scheinwerfer auf den Safe gerichtet ist, der in einem riesigen, gläsernen Wassertank versenkt ist. Eingezwängt in diesem schon bald luftleeren Safe liegt der charismatische Zauberkünstler David Copperfield. Während die Zeit verrinnt und das Wasser in den Safe sickert, erkennen wir, welches Risiko dieses unmögliche Entfesselungskunststück für Herrn Copperfield bedeutet und indirekt auch für Herrn Houdini bedeutet haben mag. Schließlich wird der Safe aus dem Tank geborgen und geöffnet. Die Tür geht auf, und Wasser schwappt auf die Bühne. Dem Publikum bleibt die Luft weg: Der Tresorraum ist leer. Stürmischer Applaus brandet auf, als plötzlich David Copperfield im perfekt sitzenden Smoking aus den Kulissen auftaucht;. Allein dieses Kunststück war den Eintrittspreis wert.

Überraschung… Wenn wir die vierte Dimension benutzen könnten – eine neue Richtung, die uns einen zusätzlichen räumlichen Freiheitsgrad bescherte -, könnte jeder von uns problemlos aus dem Tresor entkommen und in einem Leihsmoking wieder au hauchen. Mit anderen Worten: Copperfields Zaubertrick wäre nichts Besonderes mehr. In der vierten Dimension wären alle Zauberer arbeitslos, und Herr Copperfield wäre nur noch der charismatische Typ von nebenan, der unsere Hamburger brät. Die faszinierende Welt der vierten Dimension öffnet uns Wege zur Erforschung des Unbekannten, doch für ehrgeizige Zauberkünstler bleibt so manche Tür verschlossen.

Glauben Sie an Zauberei? Wie wär’s mit der vierten Dimension?
Jeder hat schon einmal von der vierten Dimension gehört, aber was genau verbirgt sich hinter diesem Begriff? Hat es nicht etwas mit Science-Fiction zu tun? Oder mit der Zeit? Sind vielleicht meine Schlüssel plötzlich dorthin verschwunden? Wie wir noch sehen werden, hat die vierdimensionale Welt in der Tat eine magische Ausstrahlung: Kaninchen könnten sich in verschlossenen Kartons materialisieren; mit einer einzigen Handbewegung ließen sich die Handschellen von unseren Handgelenken lösen, und wir könnten unsere Geschicklichkeit enorm verbessern – sogar unsere linken und rechten Körperhälften ließen sich vertauschen. Die Erforschung dieses magischen Universums ist nicht nur an sich schon faszinierend, sondern bietet uns auch Einsichten in unsere wirkliche dreidimensionale Welt.

Natürlich ist es möglich, dass unser eigentliches Universum wunderbarer und weniger banal ist, als wir glauben. Es ist möglich, dass wir in einer zusätzlichen Dimension leben, aber sie einfach nicht finden können. Vielleicht versteckt sie sich, wie unsere Schlüssel, unter einem Kissen, vielleicht weiter unten und etwas mehr nach links. Aber ungeachtet der Wirklichkeit zusätzlicher verborgener Dimensionen, hilft uns allein schon die Beschäftigung mit der Idee der vierten Dimension, die Grenzen unserer eingeschränkten persönlichen Erfahrung zu durchbrechen und uns die unbekannten wunderbaren Welten vorzustellen, die nur knapp unserer Wahrnehmung entgehen.

Was also ist die vierte Dimension? Eigentlich berührt diese Krage ein grundlegendes Problem: Was ist überhaupt eine Dimension? Um diese Frage zu beantworten, wollen wir unsere Umwelt etwas genauer betrachten.

Freiheitsgrade – wir wagen uns über unseren Raum hinaus
Die Bewegungsfreiheit unseres Körpers scheint durch den sichtbaren Raum eingeschränkt zu sein. Wir bewegen uns vor und zurück, von einer Seite zur anderen, nach oben und nach unten I Abbildung 10.1) – drei unterschiedliche Richtungen, die wir beliebig kombinieren können und die uns überall hinbringen. Folglich nehmen wir eine dreidimensionale Welt wahr. Mit einer Dimension lassen sich, etwas verschwommen formuliert, physikalische Freiheitsgrade darstellen. Und drei solcher Freiheitsgrade scheinen das Maximum für uns zu sein – im Guten wie im Bösen.

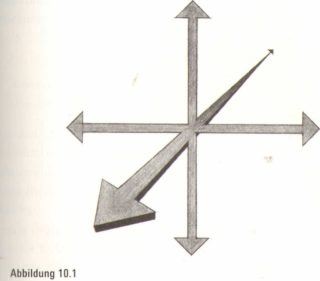
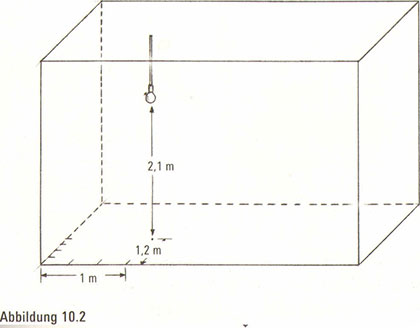
Aber wir wollen uns nun etwas genauer ausdrücken und eine Dimension so betrachten, als habe sie mit der Anzahl der Richtungen zu tun, die erforderlich sind, um einen beliebigen Ort als einen bestimmten Bezugspunkt festzulegen. Nehmen wir zum Beispiel an, wir möchten den Aufenthaltsort einer schlafenden Stechmücke angeben, die sich auf einer von der Decke herabhängenden Glühbirne niedergelassen hat, wobei wir eine bestimmte Zimmerecke als unseren Bezugspunkt wählen. Von dieser Ecke aus können wir den blutsaugenden Gast erreichen, indem wir einen Meter nach Osten, 1,2 Meter nach Norden und 2,1 Meter in die Höhe gehen – das heißt, der genaue Aufenthaltsort unserer Nervensäge lässt sich durch seine Koordinaten im dreidimensionalen Raum bestimmen (Abbildung 10.2).

Wie immer besteht die beste Möglichkeit, einer neuen Idee einen Sinn abzugewinnen, darin, die einfachsten Veranschaulichungen zu betrachten und von dort aus zu den komplizierteren voranzuschreiten. Unsere dreidimensionale Welt ist nämlich, wenngleich sie uns natürlich vertraut erscheint, weit davon entfernt, einfach zu sein.

Also ziehen wir uns für den Augenblick aus unserer dreidimensionalen Welt zurück und untersuchen stattdessen noch einfachere Welten – Welten mit noch weniger Dimensionen zum Spielen.

Wir könnten eine zweidimensional flache Tischplattenwelt in Erwägung ziehen oder sogar eine eindimensionale Linienwelt. Über wir wollen die Messlatte noch tiefer legen. Die Welt mit den geringstmöglichen Dimensionen ist ein nulldimensionaler Raum. In dieser äußerst freiheitslosen Welt sind keine Richtungen erforderlich, um einen Ort zu bestimmen. Wenn wir aber keine Angaben brauchen, um einen bestimmten Ort zu finden, dann kann man auch nicht unter verschiedenen Orten auswählen. Mit anderen Worten: Es gibt nur einen einzigen Ort in dem gesamten Raum. Also ist eine nulldimensionale Welt einfach nur ein einziger Punkt (Abbildung 10.3). Es gibt keinerlei Freiheitsgrade – wir könnten uns in der Tat nicht einmal bewegen. Müssten wir in einer nulldimensionalen Welt leben, wären wir sofort zu Hause und würden nie eine Party verpassen. Selbst mit solchen Vorteilen ist in nulldimensionales Universum, nun ja, etwas eingeschränkt. Also fügen wir eine Dimension hinzu und gönnen uns ein wenig Raum.

Als Nächstes folgt eine eindimensionale Welt. Wir könnten sie als eine Linie betrachten oder, was womöglich etwas leichter vorstellbar ist, als eine unendlich lange Straße. Das gesamte eindimensionale Universum besteht aus einer Straße, die ins Unendliche führt. Wenn wir diese Straße als Zahlenlinie auffassen (Abbildung 10.4), dann benötigen wir zum Auffinden einer Person in diesem Universum nur eine einzige Information, nämlich die Adresszahl (Abbildung 10.5).

Auf der Ebene und darüber hinaus zu Hause
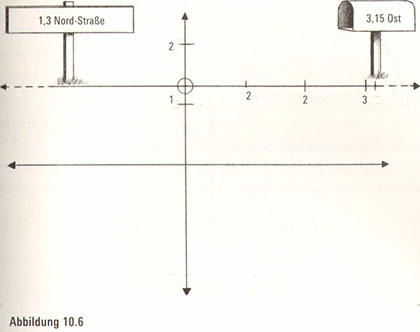
Fügen wir eine weitere Dimension hinzu, landen wir im zweidimensionalen Universum, das wir uns als Ebene oder als Tischoberfläche vorstellen können. Im zweidimensionalen Universum gibt es zwei Freiheitsgrade: Norden-Süden und Osten-Westen. Mit anderen Worten, um jemanden in der Ebene zu lokalisieren, brauchen wir zwei Informationen. Von einem zentralen Ausgangspunkt, Nullpunkt genannt, müssen wir angeben, wie weit wir in Richtung Norden oder Süden und wie weit wir anschließend in Richtung Osten oder Westen gehen müssen. Die Information über den Norden oder Süden bringt uns zur richtigen Straße. Die Ost-West-Zahl bringt uns zu dem richtigen Haus an der Straße (Abbildung 10.6).

Wenn wir uns jetzt in unsere Alltagswelt begeben, erkennen wir, dass der ganze uns umgebende Raum dreidimensional ist, da wir das absolute Minimum von drei Informationen benötigen, um eine Person genau zu lokalisieren.

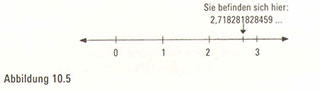
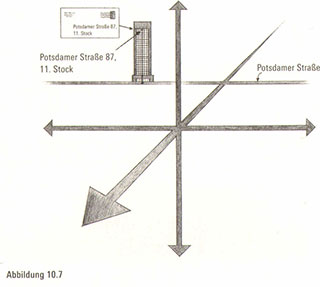
Wenn uns neue Bekannte erzählten, sie wohnten in der Potsdamer Straße 87, wüssten wir immer noch nicht genau, wo wir sie finden – sie könnten im Penthouse- Apartment wohnen, im Kellergeschoss oder irgendwo dazwischen 1 Abbildung 10.7). Wir brauchen eine zusätzliche Information – in diesem Fall das Stockwerk. In unserer dreidimensionalen Welt brauchen wir die Nord-Süd-, die Ost-West- und die Oben-unten- Richtungen.

Was ist demnach eine vierdimensionale Welt? Das ist ganz ein- i ich – es ist eine Welt, in der man genau vier Informationen benötigt, um jeden beliebigen Punkt in dieser Welt zu bestimmen. Okay, so richtig diese Behauptung auch sein mag, gibt sie uns doch keine wirkliche Einsicht in solch eine geheimnisvolle Welt.

Wir sollten daher ein Gefühl dafür entwickeln, indem wir Welten errichten und dann sehen, ob wir uns zur vierten Dimension Vorarbeiten können.

Mit Tusche auf dem Weg in die vierte Dimension
Stellen wir uns eine Linie als ein Kontinuum zusammenhängender Punkte vor. Das heißt, tauchten wir die Fingerspitze in einen Tintenklecks und zögen ihn eine Weile in eine bestimmte Richtung, entstünde eine Linie (Abbildung 10.8). Demnach ist dieser eindimensionale Raum einfach nur ein nulldimensionaler Raum, der mit Tusche ausgezogen wurde. Oder, wenn wir auf schmutzige Metaphern verzichten wollen: Der eindimensionale Raum kann als eine dichtgepackte Ansammlung nulldimensionaler Räume aufgefasst werden.

Wenn wir nun eine hingetuschte Linie in eine neue Richtung Ausziehen, lässt sich mit der Tusche eine Fläche ausziehen. Entsprechend können wir uns die Fläche als dicht gestapelte Menge von Linien vorstellen. Kommen wir zur nächsten Ebene, erkennen wir, dass wir in Analogie zu den vorangegangenen Schritten unseren dreidimensionalen Raum als das hingetuschte und ausgezogene Exemplar einer Fläche oder als dichtgepackte Menge paralleler Flächen interpretieren können. Den dreidimensionalen Raum könnten wir zwanglos als einen enormen Stapel Papier betrachten (Abbildung 10.11). Jedes Blatt ähnelt einer Fläche und hat kein nennenswertes Volumen, aber wenn sie übereinandergestapelt werden, entsteht Raum – ein riesiger rechteckiger Papierstapel, den man mit Freude betrachtet (vor allem, wenn Sie einmal das Vergnügen hatten, Papier in einem Kopiergerät nachzufüllen).

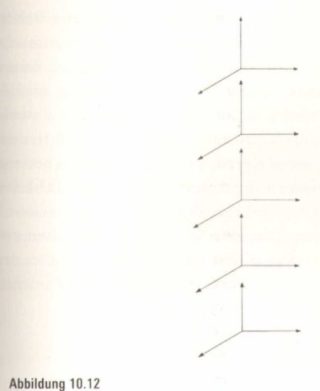
Dieses sichtbare Muster führt uns zu unsichtbaren Welten. Jetzt können wir uns also in die vierte Dimension hineintuschen. Wie machen wir das? Wir tuschen einfach den ganzen dreidimensionalen Raum hin und ziehen ihn in eine völlig neue Dimension aus – die wir nicht sehen können, da die einzigen Richtungen, die wir um uns herum wahrnehmen, in unserer dreidimensionalen Welt enthalten sind. Alternativ, aber wohl kaum hilfreicher, können wir den vierdimensionalen Raum als einen Stapel aufgeschichteter dreidimensionaler Räume betrachten (Abbildung 10.12). Diese Vorstellung ist auch nicht gerade hilfreich – denn wie könnten wir den dreidimensionalen Raum, der uns überall umgibt, stapeln und dabei nicht den normalen Raum vergrößern? Das Problem liegt darin, dass wir alles in eine völlig neue und andere Richtung stapeln oder (sollten Sie lieber mit Tusche arbeiten) ausziehen müssten, als wir es mit den augenblicklichen, uns vertrauten Richtungen tun. Was bedeutete dies?

Der vierdimensionale Raum, den wir gerade zu konstruieren versucht haben, ist zu diesem Zeitpunkt nahezu bedeutungslos. Er ist eine Abstraktion, die wir nicht wirklich begreifen können. Wie lässt sich zu einem Verständnis dieser seltsamen vierdimensionalen Welt gelangen?

Normalerweise übernehmen wir dabei die Strategie, die in dem Sprichwort zum Ausdruck kommt: Möchtest du jemanden wirklich kennenlernen, dann zieh dir seine Schuhe an, aber unglücklicherweise kennen wir niemanden, der vierdimensionale Schuhe hat. In vierdimensionalen Schuhen herumzulaufen ist eine derart befremdliche Vorstellung, dass wir nicht so recht wissen, wo wir anfangen sollen. Also was tun? Für den Augenblick lassen wir die vierte Dimension auf sich beruhen und kehren zu der zweiten Dimension zurück.

Eine zweidimensionale Welt gehört immer noch in den Bereich der Phantasie und der Science-Fiction, aber sie hat einen entscheidenden Vorteil gegenüber der vierten Dimension: Statt kompliziert und seltsam zu sein, ist sie eine seltsame Welt, die einfacher zu verstehen ist. Wir werden schon bald entdecken, dass wir beim Schlendern durch die normale zweidimensionale Tischplattenwelt Lebewesen begegnen, deren Körper und Geist zu einem besseren Verständnis unserer eigenen dreidimensionalen Persönlichkeiten und sogar der vierten Dimension beitragen. Diese Reise zu sowohl einfacheren als auch komplizierteren Science-Fiction-Welten wird uns der Einsicht näherbringen, dass unser eigenes vertrautes dreidimensionales Universum aus dem Blickwinkel anderer Dimensionen selbst eine Science-Fiction-Phantasie ist.

Schau mir in die Augen, 2-D-Kleines
Stellen wir uns ein zweidimensionales Universum vor, dessen Umfang sich auf die Oberfläche dieser Buchseite beschränkt. Machen wir uns außerdem ein Bild von den Lebewesen, die diese Welt bevölkern und ein Leben führen, das sich der Existenz anderer, vorausgegangener und nachfolgender dünner Papierblätter nicht bewusst ist. Diese Imaginationsübung trägt zur Verfeinerung unserer Fähigkeiten bei, unbekannte Bereiche zu begreifen. Welche Konsequenzen hat die Zweidimensionalität dieser papierdünnen Welt? Wie sehen ihre Bewohner aus? Was würden sie sehen? Was würden sie essen? Wo würden sie sich niederlassen? Wie würden sie uns anschauen?

Beginnen wollen wir mit der Erschaffung eines zweidimensionalen Lebewesens – nennen wir es Slim – und der Errichtung eines Hauses für ihn irgendwo in der Nähe der letzten Worte dieses Satzes. Wie würde Slim wohl aussehen, wenn wir von unserem dreidimensionalen Standpunkt aus diese Seite betrachten und auf seine zweidimensionale Welt herabschauen? Kritzeln Sie ruhig vor sich hin, wenn Sie mögen.

Vielleicht blicken wir in ein lächelndes Gesicht, wie es in Abbildung 10.13 dargestellt ist. Das entspräche etwa unseren Erwartungen, wäre aber falsch. Warum? Erinnern Sie sich bitte, dass Slims ganze Welt aus dieser Buchseite besteht. Sollte Slim diesem lächelnden Gesicht ähneln, was würde er dann sehen? Beachten Sie, dass er lediglich das Innere seines Kopfes sehen könnte. Die flache Umgebung außerhalb seines Kopfes könnte er nicht sehen, ebenso wenig natürlich die Welt über ihm (aus der wir herabschauen), weil sie für ihn nicht existiert (Abbildung 10.14). Wo befinden sich unsere Augen? Wir finden sie an der Schnittstelle zwischen unserem Körperinneren und der Außenwelt. Slims Augen müssen ich am äußersten Rand befinden, sodass er auf seine Welt hinauschauen kann.

Was ist mit Slims Mund? Sofern er nicht vorhat, sich selbst zu vertilgen, hat der gute alte Slim Probleme – denn in seiner zweidimensionalen Welt hält seine Haut Nahrung vom Mund fern. Tatsächlich bildet seine Haut – der Kreis, der seine äußere Silhouette definiert – eine Grenze, die jede Wechselwirkung zwischen Mund und Außenwelt verhindert. Unser Mund befindet sich nicht im tiefsten Inneren unseres Körpers, sondern an einem praktischeren Ort an unserer äußeren Oberfläche. Genau wie Slims eindimensionale Haut eine Grenze bildet, die seine Organe in ihm verschließt, stellen wir fest, dass unsere zweidimensionale Haut im Vergleich dazu als Grenze in unserer dreidimensionalen Welt dient.

Ausgerüstet mit diesen neuen Einsichten, verstehen wir jetzt, dass unser Blick auf Slims Welt sich ganz und gar von seinem Blick auf unsere Welt unterscheidet. Damit Slim in seiner Welt überleben kann, dürfen seine Körperteile nicht an den Stellen sein, die wir zuerst in Betracht gezogen haben. Sein Mund, seine Augen und das eine oder andere Ohr müssen sich entlang seiner Grenze befinden , weil er sie sonst nicht nutzen kann, um Nahrung zu sich zu nehmen oder Informationen zu sammeln. Beachten Sie auch, dass wir gegenüber Slim einen großen Vorteil haben. Aus unserer Sicht können wir alle Objekte auf dieser Seile – sowohl ihr Inneres als auch ihr Außeres – betrachten. Tatsächlich lässt sich nichts auf der zweidimensionalen Fläche vor unseren dreidimensionalen Augen verbergen.

Im Vergleich dazu erkennen wir jetzt, dass ein vierdimensionales Wesen – wir wollen es Di nennen – ebenfalls detaillierter auf unsere Welt blicken würde, als wir selbst es könnten. Das heißt, nichts in unserer dreidimensionalen Scheibe von Dis vierdimensionaler Welt ließe sich vor ihren Augen verbergen. Sie könnte herunter-langen und unsere inneren Organe berühren, ohne dabei unsere Haut zu verletzen. Denken Sie nur an die medizinischen Möglichkeiten, wenn wir Operationen mit diesem zusätzlichen Freiheitsgrad durchführen könnten! Um diese ungewöhnliche Perspektive zu veranschaulichen, kehren wir nun zur Zauberei zurück und erlauben uns durch Vergleiche (und vielleicht ein paar Taschenspielertricks) weitere Einblicke in die vierte Dimension.

Mit einem zusätzlichen Freiheitsgrad ein Kaninchen verschwinden lassen
Wir schauen in das leere Innere einer offenen Kiste. Dann wird sie verschlossen und verriegelt. Abrakadabra – die Kiste wird geöffnet, und heraus springt ein desorientiertes rosa Kaninchen (Abbildung 10.17). Wie lässt sich dieses erstaunliche Kunststück mit Hilfe der vierten Dimensionen aufführen?

Das Mantra Verstehe einfache Dinge gründlich ist der Schlüssel zur Lösung eines Rätsels. Wann immer wir verblüfft sind über eine Frage, die mit der vierten Dimension zu tun hat, betrachten wir zuerst analoge Versionen in niedrigeren Dimensionen. Der Rückgriff auf niedrigere, einfachere Dimensionen kann uns das Verständnis der abstrakten vierten Dimension erleichtern. Statt also mit Hilfe der vierten Dimension ein Kaninchen aus der dünnen Luft hervorzuziehen, begnügen wir uns mit dem vergleichbaren Zauberkunststück in der zweidimensionalen Tischplattenwelt, wobei der Trick in der dritten Dimension zum Einsatz kommt.

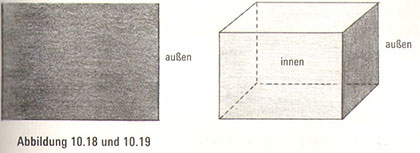
Eine verriegelte zweidimensionale Kiste ist einfach nur ein Quadrat )Abbildung 10.18). Ein Quadrat teilt eine Fläche in zwei räumliche Bereiche, nämlich in das Innere des Quadrats und in sein Äußeres, genau wie die Kiste einen dreidimensionalen Raum in zwei räumliche Bereiche trennt: in das Innere und das Äußere der Kiste (Abbildung 10.19). Jetzt nehmen wir an, dass zweidimensionale Lebewesen, die auf der Fläche leben, sich auf die verriegelte Kiste konzentrieren und sie nie aus dem Blick lassen (Abbildung 10.20). Sind wir als dreidimensionale Wesen in der Lage, die dritte Dimension zu benutzen und ein zweidimensionales Kaninchen m diese verriegelte Kiste zu setzen, ohne dass unsere Tischplattzuschauer diese Aktion bemerken?

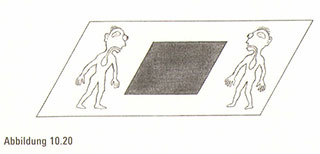
Natürlich ist es möglich – wir können das Kaninchen per Luftbrücke hineinsetzen. Denn während unser Publikum sich nur über die Oberfläche des Tisches hinwegbewegen kann, steht uns ein zusätzlicher Freiheitsgrad zur Verfügung, sodass wir über dem Tischplattenuniversum schweben und wie aus der Luft einen Panoramablick auf diese zweidimensionale Welt genießen können (Abbildung 10.21a und b). Folglich können wir die Kiste sehen und gleichzeitig sowohl die inneren als auch die äußeren Bereiche – eine Unmöglichkeit für alle Lebewesen auf der Tischoberfläche.

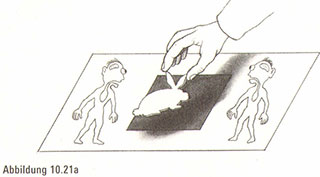
In unseren Augen ist die Kiste geöffnet. Sie existiert als ein Quadrat auf einer Tischplatte in unserer robusteren dreidimensionalen Welt, während die Fläche innerhalb des Quadrats für uns genauso zugänglich ist wie die Fläche außerhalb des Quadrats.

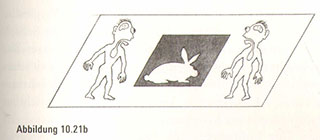
Wir könnten also einfach ein zweidimensionales Kaninchen nehmen, es genau über die Kiste halten und es auf der Tischplatte innerhalb der Kiste absetzen. Würden die Zuschauer etwas davon bemerken? Sie sähen nichts weiter als die verriegelte Kiste, da unsere Handlungen sich vollständig außerhalb ihrer flachen Welt abspielten, beachten Sie, dass das zweidimensionale Publikum nicht einmal in die Richtung zeigen könnte, aus der wir das Kaninchen herablassen würden. Sie werden erstaunt sein, wenn sie die Kiste öffnen und ein benommenes und verwirrtes Kaninchen darin erblicken (Abbildung 10.21c).

Jetzt kehren wir zu dem ursprünglichen Trick zurück, die vierte Dimension zu nutzen, um ein Kaninchen in eine verriegelten Kiste zu setzen. Dabei läuft unsere Argumentation auf Vergleiche hinaus. Da der vierdimensionale Raum aus gestapelten Schichten paralleler dreidimensionaler Räume besteht, wird wegen des zusätzlichen vierten Freiheitsgrads das Innere der Kiste sichtbar, genauso wie das Innere des Quadrats wegen unseres dreidimensionalen Blicks auf das gesamte Tischplattenuniversum sichtbar war. Folglich könnte ein Komplize in der vierten Dimension das Kaninchen per Luftbrücke aus diesem neuen Freiheitsgrad heraus in den verriegelten Tresor setzen. Das Publikum in der dreidimensionalen Scheibe des vierdimensionalen Raums würde keine verrückten Geschichten wahrnehmen, sondern würde nach der Öffnung der Kiste, die ihnen vollständig verriegelt erschienen war, die schockierende Entdeckung machen, dass ein lebendiges Kaninchen sich darin befindet.

Ein zusätzlicher Freiheitsgrad erlaubt jedem Beobachter eines niedriger dimensionierten Universums, Dinge zu sehen, die die Bewohner nicht sehen können. Die Panoramasicht ermöglicht es, alles gleichzeitig zu sehen – selbst Dinge, die den Einwohnern des niedriger dimensionierten Universums vollständig verriegelt erscheinen. Es läuft unserer Intuition als Wesen eines dreidimensionalen Universums zuwider, es könnte eine Perspektive geben, aus der es möglich wäre, in einen gut verschlossenen Tresor hineinzuschauen oder gar ein Objekt dort hineinzustellen, ohne dass wir es bemerkten. Allerdings gilt dasselbe für die Flächenbewohner auf der Tischplatte, die auf das verschlossene Quadrat schauen. Für sie ist das Quadrat vollständig verriegelt, während wir von oben auf ihre Tischplattenwelt herabschauen und das Innere des Quadrats sehen und untersuchen können, ohne jemals seine Grenzen zu berühren. Diese eindimensionale Grenze trennt die zweidimensionale Tischplattenwelt – nicht aber unsere dreidimensionale Welt – in die Fläche innerhalb des Quadrats und in die Fläche außerhalb des Quadrats. Auf ähnliche Art und Weise, nur für uns weniger sichtbar, trennt ein verriegelter Tresor unsere dreidimensionale Welt – nicht aber eine vierdimensionale Welt – in den Raum innerhalb des Tresors und in den Raum außerhalb des Tresors. Wenn vier Dimensionen zur Verfügung stehen, existiert eine verschlossene dreidimensionale Kiste lediglich in einer Scheibe des Raums.

Schnürsenkel ohne Tränen entknoten Angenommen, wir haben es mit einer geschlossenen Schleife eines Schnürsenkels mit einem Knoten darin zu tun (Abbildung 10.22).

Es ist unmöglich, allein durch Bewegung des Schnürsenkels den Knoten zu lösen. Die einzige Möglichkeit, einen wirklichen Knoten in der Schleife zu lösen, besteht darin, die Schnur durchzuschneiden und die Enden wieder zu verschließen. Stünde uns jedoch die vierte Dimension zur Verfügung, ließe sich jedes durch Knoten entstandene Durcheinander lösen, ohne dass wir jemals zu einer Schere greifen müssten. Wie das? Kehren wir erneut zu einer zweidimensionalen Version dieser Frage zurück. Eigentlich kann es in einem Tischplattenuniversum gar keine Knoten gelten. Alle Objekte in diesem Universum liegen flach auf der Ebene, während hingegen für Knoten eine dritte Dimension erforderlich ist – hier müssen die Schnüre übereinanderliegen (Abbildung 10.23).

Aber wir können die geistige Einstellung hinter der Entknotungslösung einfangen, indem wir uns eine giftige Tsetsefliege im Tischplattenuniversum anschauen. Um diese monströse Stechfliege zurückzuhalten, riskieren besorgte Bürger in der zweidimensionalen Welt ihr Leben und fangen den Schädling mit einem zweidimensionalen Lasso ein. Sie legen die Schnur um die Tsetsefliege und erzeugen so eine Schleife, in der die Fliege vom Rest der Fläche abgeriegelt ist. (Dieser Teil unserer Geschichte – sowie alle weiteren Entwicklungen – lassen sich in Form eines Comicstrips in Abbildung 10.24 betrachten.)

Alles ist in Ordnung, bis eine dreidimensionale Terroristin beschließt, das Leben aller Bürger des Tischplattenuniversums zu bedrohen, indem sie die Tsetsefliege freilässt. Sie weiß allerdings, dass die Fliege auch für dreidimensionale Terroristen eine Gefahr darstellt. Deshalb muss sie ihren Plan so ausführen, dass sie die Fliege nicht ganz berührt. Schließlich kommt sie auf die Idee, ein Stück der Schnur anzuheben, das um die Fliege herumgelegt ist.

Was sehen jetzt die Flächenleute? Aus ihrer Perspektive verschwindet plötzlich ein Stück der Schnur. Sie ist nicht durchgeschnitten worden, aber für die Bürger des Tischplattenuniversums sieht es so aus, als würde ein Abschnitt der Schnur fehlen. Natürlich sieht es auch für die Tsetsefliege so aus, sodass es ihr gelingt, durch die Lücke zu entkommen und die Bewohner der Fläche wieder zu terrorisieren.

An diesem Punkt kann die Übeltäterin das Stück Schnur wieder zurück auf die Tischoberfläche legen. Für die Bewohner sieht es letzt so aus, als sei die durchschnittene Schnur auf geheimnisvolle und Weise wieder ganz geworden. In Wirklichkeit aber war, wie wir wissen, die Schnur niemals durchschnitten gewesen – sie war lediglich, außer Sichtweite der Tischplattenbewohner, in eine neue Dimension angehoben worden. Und so kommen wir zum Ende unserer traurigen Geschichte, die ein furchterregendes Bei-spiel für MDW ist – multidimensionale Waffen.

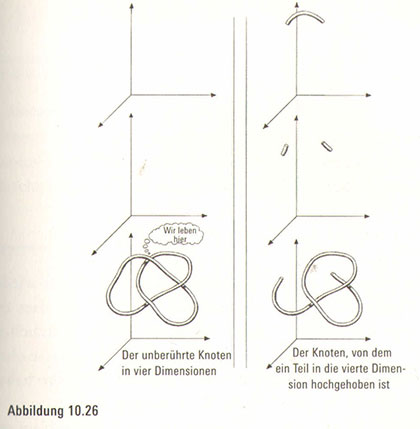
Und nun sind wir bereit, die Schnürsenkelschleife mit dem Knoten in Angriff zu nehmen, wobei die vierte Dimension uns als Ersatz für das Aufschneiden dient. In diesem höherdimensionalen Kontext wollen wir die Strategie unserer Übeltäterin anwenden. Das heißt, wir lassen ein vierdimensionales Wesen ein Stück Schnur in die vierte Dimension hochheben. Dann wird nämlich dieses Stück Schnur jenseits des dreidimensionalen Raums liegen, auf den unsere Sicht beschränkt ist. Deshalb wird es für uns so aussehen, als sei dieses Stück weggeschnitten worden (.Abbildung 10.26). In Wirklichkeit bleibt die Schnur intakt. Ein Teil davon hat sich lediglich in parallele dreidimensionale Räume bewegt, die unsichtbar für uns sind. In unserer dreidimensionalen Welt jedoch bleibt die Tatsache bestehen, dass der Schnur ein Abschnitt fehlt, und folglich können wir leicht den Knoten lösen (Abbildung 10.27). Jetzt lässt
unser Freund in der vierten Dimension diesen Abschnitt wieder herab in unsere Welt.

Wir nehmen die Illusion wahr, dass die Schnürenden sich wieder vereinen (Abbildung 10.28). Plötzlich ist die Schnur wieder eine Schleife – aber jetzt glücklicherweise ohne diesen lästigen Knoten. Mit Hilfe der vierten Dimension haben wir den Knoten gelöst, ohne eine Schere zu benutzen!

Die Magie der vierten Dimension – Lotto und Glücksspiele Tipps Teil 1