Warum wir die Zukunft nicht Voraussagen können – Lotto und Glücksspiele Tipps Teil 2

Warum wir die Zukunft nicht Voraussagen können – Lotto und Glücksspiele Tipps Teil 1

Auch das noch: Beide Spalten sind falsch!
Wir können dieses überraschende Beispiel für Chaos jetzt nicht einfach links liegen lassen, ohne ein wichtiges Merkmal der beiden Zahlenspalten zur Kenntnis zu nehmen: Nach ein paar Dutzend Schritten liefern beide Spalten völlig falsche Ergebnisse. Nun ist es nicht etwa so, dass die erste Spalte, die ein paar mehr Ziffern hinter dem Komma speichert, richtig ist, während die andere falsch ist. In Wirklichkeit haben sich beide ganz und gar von der eigentlichen Antwort entfernt. Ja, es gibt eine konkrete Antwort, und es ist keine mathematische Zauberei dabei im Spiel. Wenn wir also mit 0,5 anfangen, die Zahl quadrieren und 2 davon abziehen, gibt es ein wahres Ergebnis. Wenn nun dieses wahre Ergebnis quadriert wird und wir wieder 2 subtrahieren, dann ergibt das eine einzige absolut korrekte Antwort, und so geht es immer weiter. Aber diese absolut richtigen Ergebnisse haben schon bald Tausende, Millionen, Milliarden und Billionen Ziffern hinter dem Komma.

Nur zum Spaß haben wir einen Computer benutzt, um die ersten acht völlig korrekten Antworten auf das wiederholte Verfahren des Quadrierens und Subtrahierens von 2 mit dem Anfangswert 0,5 zu notieren.
Erste Iteration * -1,75
Zweite Iteration = 1,0625
Dritte Iteration = -0,87109375
Vierte Iteration = -1,2411956787109375
Fünfte Iteration = -0,45943328714929521083831787109375
Sechste Iteration =
-1,7889210546591932520800981298858545187613344751298427581787109375

Siebente Iteration = 1,200238539802296029103616942146559932 82994385584519957749445652778467437691 3057583967901070787220874080958310514 688491822890625

Achte Iteration = -0,559427447571657705178721205866417747 67887466759766547362611062488433478134 64738475513323533i98234707329445298264
57618958958249397529981910451892249605 03378673326317854984854513373905558588
17016976682057746937708347391947361071
37373734375811181962490081787109375

Wie Sie sehen, hat die achte Antwort 256 Stellen hinter dem Komma. Um eine Zahl exakt wiederzugeben, müssen alle ihre Ziffern dargestellt und berücksichtigt sein. Wie wir bereits festgestellt haben, machen Fehler in den hintersten Ziffern wirklich etwas aus. Aber Excel muss an irgendeiner Stelle hinter dem Komma die Zahlen abrunden, sodass sich diese unvermeidlichen Rundungsfehler bald fortpflanzen und sich die von Excel berechnete Antwort extrem von der korrekten Antwort unterscheidet. Deswegen sind eine Menge Zahlen, die wir in den Excel-Spalten sehen, völlig sinnlos. Sie haben überhaupt keinen Bezug zu den real existierenden richtigen Antworten, die wir allerdings unmöglich genau errechnen können. Um nämlich eine Zahl präzise bestimmen zu können, brauchen wir alle ihre Ziffern.

Nebenbei bemerkt, gibt es auch für Leser, denen der Umgang mit Excel nicht so geläufig ist, eine Möglichkeit, dieses Zahlenchaos selbst zu erleben. Wir führen einfach das am Anfang beschriebene Szenario durch und benutzen dafür zwei Taschenrechner unterschiedlicher Marken mit jeweils anderer Dezimalgenauigkeit. Wenn wir dann das Quadrierungs- und Subtraktionsverfahren auf beiden Rechnern wiederholen, werden wir zu Zeugen des Chaos in Aktion. Und wie in unserem Experiment mit der Tabellenkalkulation werden die Antworten nach einigen Dutzend Wiederholungen völlig sinnlos. Unser Excel-Experiment ist im Wesentlichen dasselbe, das bei der unabsichtlichen Entdeckung des mathematischen Chaos ausgeführt wurde.

Durch Zufall herbeigeführtes Chaos
Unser Paradigma vom Chaos in der Welt beschwört Bilder von Wirbelstürmen herauf, die vom Schmetterlingseffekt ausgelöst werden. Und wie das Schicksal so spielt, entdeckte ein Meteorologe das mathematische Chaos durch einen glücklichen Zufall. In den 1960er Jahren arbeitete Edward N. Lorentz als Meteorologe am MIT (Massachusetts Institute of Technology) an mathematischen Modellen für die Wettervorhersage. Dafür benutzte er die primitiven Computer der damaligen Zeit. Zunächst beschrieb er das Wetter anhand einer Liste mit numerischen Daten. In seinem Modell wurden nun diese Daten benutzt, um eine Zahlenliste zu erzeugen, die das Wetter für den nächsten Zeitabschnitt Vorhersagen sollte. Anschließend wurden diese Werte erneut in die mathematischen Formeln eingesetzt, um ähnliche Werte für den nächsten Zeitabschnitt zu erzeugen und so weiter.

Eines schönen Tages, als Lorentz gerade sein Wettervorhersagesystem laufen ließ, wurde er plötzlich unterbrochen. Anschließend musste er ein paar der letzten Werte noch einmal eingeben und den Prozess neu anlaufen lassen, nachdem einige Wiederholungen bereits vollständig ausgeführt worden waren. Statt alle Ziffern neu einzutippen, wollte er sich den Aufwand sparen und rundete die Zahlen ab in dem Glauben, es dürfte eigentlich keinen Unterschied machen, wenn er die sechste oder siebente Stelle wegließe. Als sein Modell jedoch wieder anlief, entdeckte er, dass das Abrunden dieser Werte zu radikal anderen Wettervorhersagen führte.

Innerhalb seines mathematischen Wettermodells war Lorentz sein eigener brasilianischer Schmetterling. Mit anderen Worten: Er erkannte, dass sein Modell bei der Eingabe von Werten, die erst ab der sechsten oder siebenten Stelle hinter dem Komma nicht mehr übereinstimmten, schon nach wenigen Wiederholungen erstaunlich unterschiedliche Werte erzeugte. Folglich fand er heraus, dass die übliche Praxis, die Zahlen bis auf ein paar relevante Ziffern abzurunden, bei der Ausführung von Wiederholungsverfahren zu erheblich unterschiedlichen Ergebnissen führte. Lorentz erkannte, dass sein Wetterbeschreibungssystem eigentlich ein Beispiel für eine neue mathematische Entdeckung war. So war er völlig unbeabsichtigt zum Vater des Chaos geworden.

Die Zukunft Vorhersagen
Wir haben iterative Systeme erkundet – Prozesse, die von einem Wert ausgehen, eine Prozedur durchführen, um eine Antwort zu erzeugen, und diese Antwort als nächsten Ausgangspunkt benutzen, um dieselbe Prozedur noch einmal ablaufen zu lassen und somit den ganzen Prozess immer wieder neu in Gang zu setzen, sodass ein veritabler Zahlenstrom zustande kommt. Unser erstes iteratives System war das offenbar sinnlose Verfahren des wiederholten Quadrierens und Subtrahierens von 2.

In Wirklichkeit lassen sich mit ähnlichen Verfahren Populationen und sogar die Koordinaten von Planeten bestimmen. In jedem dieser Beispiele erlaubt uns die Kenntnis der aktuellen Bevölkerungszahl oder der Position des Planeten die Anwendung von Verfahren, um die Bevölkerung oder die planetaren Positionen im nächsten Zeitabschnitt zu berechnen. Wir können diesen Prozess beliebig oft wiederholen. Inzwischen wissen wir allerdings, dass die Ergebnisse nach einigen Iterationen im Grunde sinnlos geworden sein könnten. Auf unsere Wirklichkeit bezogen, bedeutet dies, dass iterative Modelle von Systemen wie Wetter, Populationen und gar Planetenbewegungen anfällig für die Erzeugung chaotischen Unsinns sind und nicht zu verlässlichen langfristigen Vorhersagen führen. Das Fazit ist: Wir verstehen jetzt, warum wir von unseren Wetterfröschen in Funk und Fernsehen keinen verlässlichen Wetterbericht für die nächsten dreißig Tage erwarten können.

Wir leben im physikalischen Chaos
Es geht um die klassisch mechanischen Bewegungsmodelle bewegter Objekte. Von schwingenden Pendeln über springende Bälle bis zu Magnetfeldern und Flüssigkeitsströmen beschreibt die klassische Physik aufs genaueste, was dabei passiert. Die algebraischen Formeln, die solche physikalischen Systeme modellieren, sind die Korrektheit schlechthin. Allerdings ähneln die algebraischen Ausdrücke denen, die uns in unseren Excel-Experimenten begegneten. Ist es möglich, dass die physikalischen Systeme, deren Verhalten durch die verlässlichen Formeln ausgedrückt wird, in Wirklichkeit chaotische Eigenschaften zeigen? Das heißt, werden wir physikalisches Chaos finden, oder ist diese ganze Geschichte mit dem Chaos lediglich abstrakte mathematische Zauberei? Kommen wir also auf den Punkt.

Phnom.. Der Pfad eines schwingenden Pendels ist eines der regelmäßigsten Muster, das wir kennen. Tatsächlich war das Pendel jahrhundertelang der Grundbestandteil von Uhren. Rekonstruierten wir die Bahn eines Pendels, sähen wir einen vorhersagbaren Pfad (Abbildung 2.4). Wir wollen nun ein geringfügig verändertes Objekt betrachten, das als Doppelpendel bekannt ist. Es ist ein einfaches Pendel, das am Ende eines zweiten Pendels schwingt (Abbildung 2.5). Bestimmt würden wir jetzt ein ähnlich regelmäßiges Muster erwarten, nach dem wir unsere Uhr stellen könnten.

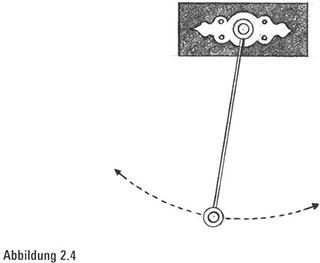
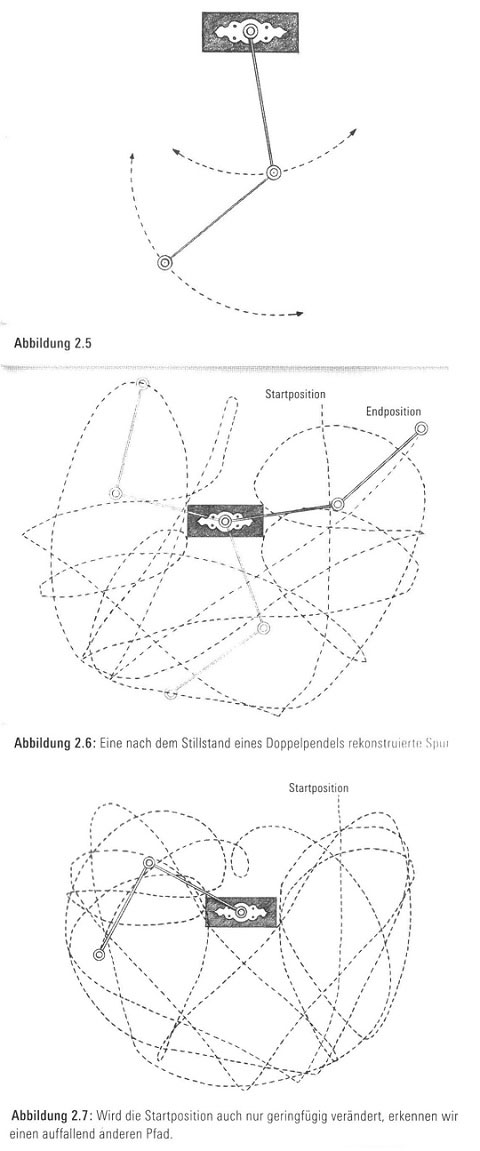
Überraschung. Es herrscht Chaos. Der am Ende eines Doppelpendels registrierte Pfad ist ein unregelmäßiger Schnörkel (Abbildung 2.6). Es gibt kein einfaches, vorhersagbares Muster. Und wenn wir von einer noch so geringfügig anderen Position aus anfangen, sieht der chaotische Schnörkel dennoch völlig anders aus (Abbildung 2.7). Falls Sie animierte Simulationen sehen möchten, starten Sie im Internet eine Suche nach Doppelpendel.

Tropfender Wasserhahnt. Ließen wir eine winzige Menge Wasser aus dem Wasserhahn ins Becken tropfen, fänden wir zum Takt der Tropfen mit Sicherheit auch einen regelmäßigen Rhythmus.

Überraschung. Wenn wir den Wasserhahn vorsichtig aufdrehen, stellen wir fest, dass es bei manchen Konstellationen zwar regelmäßig tropft, nach weiteren Manipulationen am Hahn aber ein unvorhersagbares Tropfmuster entsteht, bei dem die Tröpfchen in unregelmäßigen, chaotischen Intervallen fallen. Dieser einfache tropfende Wasserhahn bestätigt unsere Ahnung, dass undichte Stellen im Badezimmer das reinste Chaos verursachen.

Magneten. Betrachten wir ein durchhängendes Pendel mit einem magnetischen Ende, das frei in jede Richtung schwingen kann, und eine Platte mit drei darauf befestigten Magneten, die das Pendel anziehen können (Abbildung 2.8). Nähert sich das Pendel einem der drei Magneten, ist natürlich die Anziehungskraft dieses Magneten entsprechend stärker ausgeprägt. Und wir erwarten, dass die Spitze des Pendels ein vorhersagbares, regelmäßiges Muster beschreibt.

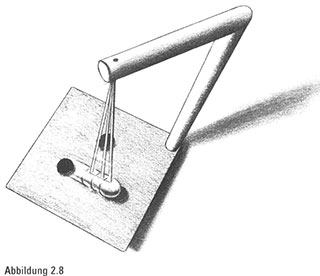
Überraschung. Schon wieder sind wir mit dem Chaos konfrontiert. Das aufgespürte Muster ist unregelmäßig, sprunghaft und unvorhersagbar. Bei drei unterschiedlichen, aber sehr nahe beieinanderliegenden Startpositionen wird die magnetische Spitze jeweils von einem anderen Magneten angezogen, sodass drei sehr unterschiedliche Muster entstehen (Abbildung 2.p).
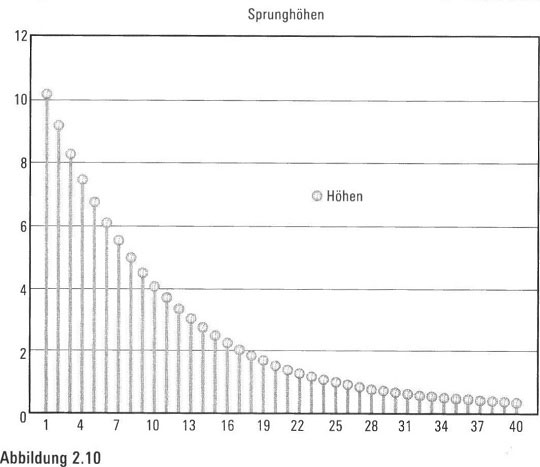
Springender Ball. Wenn wir einen Ball fallen und vom Boden hochspringen lassen, werden wir ein regelmäßiges Muster verringerter Sprunghöhen registrieren (Abbildung 2.10).

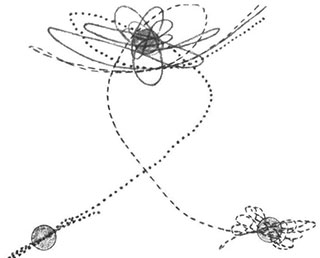
Abbildung 2.9: Drei nahe beieinanderliegende Startpositionen / Die Simulation beschreibt die Pfade eines magnetischen Pendels für drei verschiedene Startpunkte. Pendelspitze wird schließlich jeweils von einem anderen Magneten angezogen.

Betrachten wir jedoch einen Kolben im Rohr, wobei der Kolben sich mit regelmäßiger Geschwindigkeit auf und ab bewegt. Angenommen, wir lassen einen Ball jetzt so fallen, dass er auf dem sich bewegenden Kolben herauf- und herunterspringt (Abbildung 2.11).

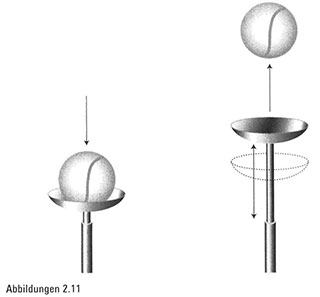
Gibt es einen Rhythmus für die Höhen, die der springende Ball erreicht?

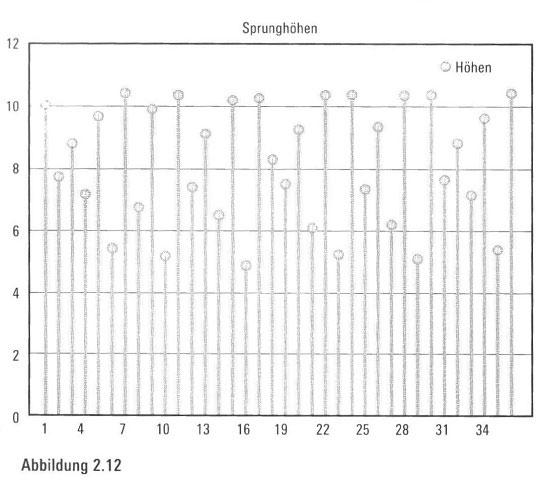
Überraschung. Und wieder herrscht das Chaos: Das Muster der Sprunghöhen des Balls ist chaotisch (Abbildung 2.12). Inzwischen können wir allerdings wirklich nicht mehr erwarten, dass irgendein Leser angesichts des Chaos überrascht ist. Und genau das ist der springende Punkt.

Deshalb spiegelt sich das Chaos in der Tat im wirklichen Leben wider. Unsere Beispiele – Pendel, tropfender Wasserhahn, springende Bälle – sind physikalische Manifestationen des Zahlenchaos, über das wir schon gesprochen haben. Sie sind nur einige von vielen Veranschaulichungen eines weitverbreiteten Phänomens. Vor der Veröffentlichung der Lorentzschen Beobachtungen glaubten die Physiker im Allgemeinen daran, dass die von der klassischen Mechanik beschriebene Welt eher deterministisch sei. Doch im Laufe der 1970er und 1980er Jahre fingen die Mathematiker und Physiker allmählich an, die Bedeutung des Chaos-Konzepts zu untersuchen. Und schon bald stellte sich heraus, dass das Chaos – das heißt, die Abhängigkeit von den Anfangsbedingungen – sowohl in den mathematischen Beschreibungen der Welt als auch in der Welt selbst ein allgemein verbreitetes Phänomen war. Da selbst einfache mathematische Systeme Chaos aufweisen und zur Unvorhersagbarkeit führen, waren die Physiker gezwungen, die Vorstellung zu akzeptieren, das Chaos sei zwingend ein grundlegendes Merkmal der Natur.

Diese Einsicht hat weitreichende Konsequenzen, selbst für die Wissenschaftstheorie – das heißt für unser Konzept der fundamentalen Grenzen wissenschaftlicher Erkenntnisfähigkeit. Früher glaubten viele Physiker, die Quantenphysik zeige auf grundlegender Ebene die Ungewissheit wissenschaftlicher Wahrheit. Diese Perspektive mag grundsätzlich stimmen, aber vielleicht verringert das Chaos in der klassischen Mechanik unsere Fähigkeit zur Vorhersage der Zukunft physikalischer Systeme in einem größeren Ausmaß als die Quantenmechanik. Beim Messen physikalischer Aspekte der Welt werden immer Ungenauigkeiten auftreten, und diese Ungenauigkeiten werden unweigerlich verstärkt, sodass sie dramatische Unterschiede zu unseren Vorhersagen über die Ereignisse in der nahen Zukunft erzeugen werden. Aus dem Chaos lässt sich schließen, dass unser Potenzial stark eingeschränkt ist, das künftige Verhalten selbst einfacher physikalischer Phänomene vorherzusagen.

Schlussfolgerungen aus dem Chaos
Bei unserem Versuch, die Welt zu verstehen, entwickeln wir manchmal ganz vernünftige mathematische Modelle, die es uns erlauben, die Zukunft auszuloten. Wir geben uns der Hoffnung hin, dass die Bedingungen und Einflüsse in unserem Umfeld es uns gestatten, die Welt in ihrer lebendigen Entwicklung zu erfassen – als Zukunft, die von den gegenwärtigen Umständen bestimmt wird. Aber selbst wenn wir uns diese Modelle in der abstrakten Umgebung reiner mathematischer Logik betrachten, in der nichts von der Wahrheit abweicht und jede Kalkulation fehlerlos und präzise ist, stellen wir immer noch fest, dass unser Blick auf künftige Aus
sichten getrübt ist. Die Abhängigkeit von Anfangsbedingungen in iterierten oder wiederholten mathematischen Prozessen führt geradewegs ins Chaos. Da iterierte Systeme im Allgemeinen zur Beschreibung von Verhaltensweisen in unterschiedlichen Bereichen eingesetzt werden, sind die Konsequenzen dieses Studiums weitreichend. Sie beeinflussen unser Verständnis vom Wetter, von Populationen, Flüssigkeitsdynamik, Wirtschaftswissenschaft, Aktienmärkten, oszillierenden chemischen Reaktionen, elektrischen Netzwerken und sogar von Herzrhythmen und Gehirnwellen.

Wir können den Schein des Feuers der fernen Zukunft des-halb nicht sehen, weil wir eine so enorme Menge winziger Abweichungen auf dem Weg dorthin ansammeln, dass das Endziel hinter Nebelschleiern verborgen bleibt. Selbst die Mathematik ist in ihrer Vollständigkeit und Präzision den Gefahren winziger Unterschiede bei den Anfangsbedingungen ausgesetzt, die – durch die Mühle wiederholter Anwendung gedreht – multipliziert und verstärkt werden und uns in die Irre führen. Gibt es einen Trost? Nur den, dass die Modelle geringfügig besser werden, sodass die unvermeidlichen Abweichungen aufgeschoben und künftigen Generationen überlassen werden – sollen die sich doch mit dem Chaos herumschlagen!