
Das Zusammenwirken von Natur und Zahl – Lotto und Glücksspiele Tipps Teil 1
Eine Suche nach Mustern
Wenn wir uns nicht auf das Unerwartete einsteilen, werden wir es nie finden.
Heraklit
Offensichtlich … Ein Quadrat von 8×8 Einheiten hat eine Fläche von 64 Quadrateinheiten. Natürlich können wir es nicht einfach in Puzzlestücke zerschneiden und es dann neu zu einem Rechteck mit 5X13 Einheiten anordnen, was einer Fläche von 65 Quadrateinheiten entspricht (Abbildung 6.1).
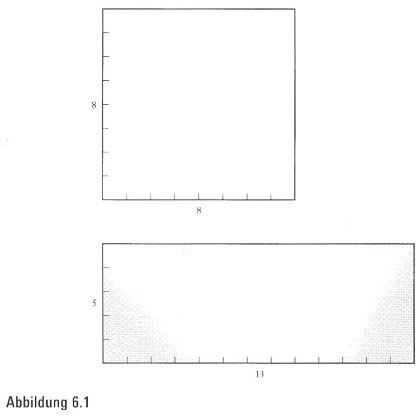
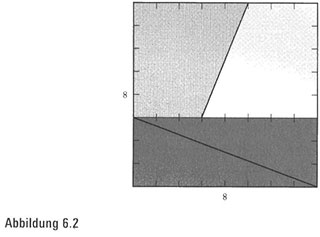
Überraschung … Ziehen Sie in Erwägung, das Quadrat so in vier Stücke zu zerschneiden, wie es in Abbildung 6.2 dargestellt wird. Und versuchen Sie jetzt, das Kunststück zu vollführen, aus ihnen das Rechteck zu bilden. Natürlich funktioniert das nicht wirklich, weil dieselben Stücke in neuer Anordnung dieselbe Fläche haben müssten. Aber Sie könnten, mit dem allerschmalsten Schlitz entlang der Diagonalen, ein sehr überzeugend wirkendes Rechteck zusammenstückeln. Wie diese geometrische Illusion funktioniert, ist Teil einer Geschichte, die mit einer Ananas anfängt und mit bildender Kunst endet.
Nicht nur in der Mathematik, sondern auch im Leben geschieht es recht häufig, dass wir Muster finden, wenn wir sie suchen. Und sobald wir Muster aufdecken, entstehen – wie von Zauberhand – zuvor unsichtbare Merkmale, sodass plötzlich prachtvolle Strukturen im Brennpunkt unserer Neugier stehen.
Lust auf Ananas
Wo finden wir Inspirationen für große Entdeckungen? Wir könnten annehmen, dass tiefgründige Einsichten nur in gut ausgestatteten Labors stattfinden oder in geschmeidigen Ledersesseln, umgeben von staubigen Wälzern in den Naturschutzgebieten von Elfenbeintürmen. Unsere Geschichte beginnt jedoch in einem bescheideneren – vielleicht sollten wir sagen: fruchtbareren – Ambiente, nämlich in der Obstabteilung eines Lebensmittelladens. Dabei wollen wir unser Augenmerk vor allem auf eine besonders appetitliche tropische Frucht richten – die Ananas.
Ananas sind exotisch, stachlig und köstlich zugleich. Während wir uns normalerweise auf den Geschmack konzentrieren, den uns ihr Inneres zu bieten hat, wollen wir hier nur die äußere Attraktivität betrachten.
Wir beginnen einfach mit einem Blick auf die Ananas. Es wäre schön, wenn alle Leser selbst eine Ananas kaufen und sie mit uns zusammen erforschen könnten. Als zusätzlichen Anreiz – obwohl natürlich jede mit mathematischen Ideen verbrachte Stunde ohnehin eine glückliche Stunde ist – sollten Sie die Gelegenheit betrachten, sich Pina-Colada-Drinks zu mixen, wenn wir die mathematischen Merkmale aus unseren Ananas herausdestilliert haben. Zum Wohl!
Betrachten wir die eindrucksvolle Fassade der Ananas, stellen wir schnell das überraschende Merkmal fest, dass die Oberfläche der Frucht von einer Menge Spiralen zerfurcht ist. Wir können mit dem Finger über die Rillen fahren, die von den hübsch angeordneten Buckeln erzeugt werden, und dabei die spiralenförmigen Bereiche ertasten, die die Ananas umrunden. (Die versteckten Spiralen werden in Abbildung 6.3b dargestellt.) Wenn wir jetzt die Ananas in die Hand nehmen und ihre knubbelige Oberfläche betrachten, sehen wir keine zufälligen Buckel mehr. Die spiralförmigen Linien, die stets da waren, aber unbemerkt blieben, scheinen auf einmal ganz offenkundig da zu sein.

Haben wir erst einmal die Struktur entdeckt und schauen genauer hin, entdecken wir oft noch mehr. In diesem Fall offenbart ein zweiter Blick auf unsere Ananas eine zweite Folge paralleler Spiralen, die in umgekehrter Richtung verlaufen (.Abbildung 6.3c). Diese beiden miteinander verflochtenen Spiralmengen erzeugen die wunderschöne, vertraute Ananasoberfläche.

Aufs Zahlen zählen
Wie wir im vorangegangenen Kapitel beobachtet haben, öffnet das Zählen häufig unsere Augen für neue Erkenntnisse. Da wir nun Mengen von Spiralen auf der ganzen Oberfläche der Ananas entdeckt haben, könnten wir den Schritt von der qualitativen Erkenntnis (Es gibt viele Spiralen) zur quantitativen Auswertung (Die genaue Anzahl der Spiralen lautet…) machen. Wir wollen daher die Spiralen zählen, die wir in jeder der beiden Richtungen sehen.
Spiralen abzuzählen ist in Wirklichkeit viel schwieriger, als Sie vielleicht denken. In Abbildung 6. je haben wir diesen Schritt etwas vereinfacht, aber wir bitten Sie dringend, die Zählvorgänge hier mit denen an ihrer eigenen Ananas zu vergleichen. Oder wenn Sie die 3,99 Euro nicht investieren wollen, nehmen Sie im Lebensmittelladen eine Ananas nach der anderen in die Hand und zählen Sie die Spiralen. So werden Sie bestimmt die Aufmerksamkeit der anderen Kunden auf sich lenken.
Überraschung. Die Zählungen auf den meisten gesunden, gutgerundeten Ananas ergeben 8 und 13 Spiralen. Die erste Überraschung besteht darin, dass die in eine Richtung verlaufenden Spiralen zahlreicher sind als die in die andere Richtung orientierten Spiralen. Die zweite Überraschung ist, dass im Wesentlichen jede Ananas die gleichen Zählergebnisse für Spiralen aufweist.

Ein Spiralenwirbelwind
Wenn wir unsere Augen für Spiralen öffnen, finden wir sie überall. In der Natur gibt es Spiralen in Hülle und Fülle. Wenn wir den Lebensmittelladen verlassen und durch den Garten schlendern, offenbart uns ein schneller Blick ins feurige Zentrum einer Rudbeckie (Kegelblume) sogleich zwei Einheiten miteinander verflochtener Spiralen (Abbildung 6.4). Wie können wir unsere Begeisterung zügeln, sie zu zählen? Überhaupt nicht, und schon sind wir dabei (Abbildung 6.5a).
In der einen Richtung sehen wir 13 Spiralen – was für ein erstaunlicher Zufall angesichts der Tatsache, dass eine der Zählungen auf der Ananas ebenfalls 13 ergeben hatte. Jetzt können wir schon gar nicht aufhören und zählen die Spiralen in der anderen Richtung (Abbildung 6.5b). Hier kommen wir auf 21 Stück.

Bis jetzt wirbeln also die Zahlen 8,13 und 21 durch unseren Kopf.

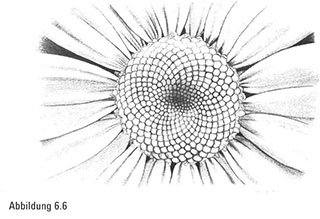
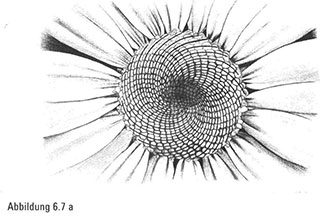
Wenn wir uns nun das wunderschöne Gänseblümchen anschauen, könnte es passieren, dass wir dem romantischen Drang nachgeben, die weißen Blütenblätter abzuzupfen und dabei vor uns hin zu murmeln: Sie liebt mich …, oder: … er liebt mich nicht. Ob wir uns nun aber dem Drang zu zupfen hingeben oder nicht, auf jeden Fall blicken wir in das sonnige Lächeln des runden gelben Zentrums, das aus miteinander verflochtenen Spiralen besteht (Abbildung 6.6). Sobald wir vertraute Objekte nur ganz genau betrachten, wird sich uns eine ganze Welt von Strukturen offenbaren. Während wir die Spiralen des Gänseblümchens zählen, kommen wir auf 21 in der einen Richtung (Abbildung 6.1a) – erneut ein erstaunlicher Zufall, da diese Zahl mit einer unserer vorangegangenen Zählungen übereinstimmt -und 34 in der anderen Richtung (Abbildung 6.1b). Somit ist die Zahlenfolge der Natur auf 8, 13, 21, 34 angewachsen.
Wenn wir einen Pinienzapfen in die Hand nehmen und dessen Spiralen zählen, kommen wir auf 5 und 8 Spiralen – wobei die 8 noch für eine weitere kosmische Zahlenübereinstimmung mit der Ananas sorgt.
Diese ständig sich weiter ausdehnende Menge von Zufällen führt uns zu der Frage, ob vielleicht eine unsichtbare Struktur damit verbunden ist. Die Zahlenliste, mit der uns die Natur versorgt hat, lautet bis jetzt 5, 8, 13, 21, 34. Betrachten wir diese Zahlenfolge als ein kollektives Ganzes, tritt ein erstaunliches Muster zutage. Erkennen Sie es?
Überraschung. Sobald wir die ersten beiden Zahlen auf unserer Liste addieren, erhalten wir die nächste Zahl. Die zweite und dritte Zahl ergeben die vierte Zahl; die Summe der dritten und vierten ergibt die fünfte Zahl. Unglaublich – diese Zahlen sind die Ergebnisse verschiedener Auszählungen von Spiralen, die in unterschiedlichen Früchten und Blumen auftreten, und dennoch stellen die Zahlen auf der Liste ein Muster dar.
Wenn wir von der praktischen Natur zur abstrakten Mathematik überwechseln, sollte es uns durch Beachtung des Musters gelingen, die Zahlenfolge fortzuführen. Die nächsten Terme wären 21 + 34, was 55 ergibt, gefolgt von 34 + 55 = 89, dann 144 und 233, und so ginge es immer weiter. Außerdem lädt uns das Muster dazu ein, rückwärts zu reisen – das heißt, vor der 5 muss eine 3 stehen (da 3 + 5 = 8), und vor der 3 steht eine 2, der eine 1 vorangeht, der wiederum eine 1 vorangeht. Auf diese Art und Weise haben wir eine Zahlenliste erzeugt, die folgendermaßen beginnt:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233
und bis in alle Ewigkeit so weitergeht. Diese Liste ist zustande gekommen, weil wir ein in der Natur gefundenes Saatkorn eines Musters in die abstrakte Welt der Mathematik verpflanzt haben und dort wachsen ließen.
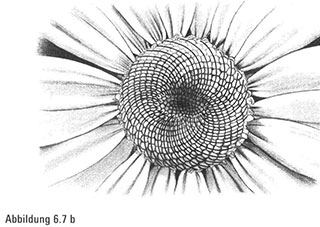
Diese abstrakten Zahlen haben Auswirkungen auf die Wirklichkeit. Unsere Zahlenfolge lässt sich in die Wärme unserer Alltagswelt zurückholen, auf dass sie uns neue Einblicke in die Natur vermitteln möge. Wo sollten wir suchen? Es liegt auf der Hand, dass dafür Objekte in Betracht kommen, die einem Tannenzapfen, einer Ananas, einer Rudbeckie und einem Gänseblümchen ähneln, aus deren Spiralen sich die Zahlenfolge ergab. Und wenn wir uns jetzt die riesige Sonnenblume anschauen, werden wir nicht enttäuscht. Wie viele Spiralen können wir entdecken?
Angesichts unserer vorausgegangenen Übereinstimmungen beim Zählen könnten wir jetzt auf 34 und 55 tippen oder auf 55 und 89. Es stellt sich heraus, dass diese Vermutungen richtig sind – bei kleinen Sonnenblumen kommen wir auf 34 und 55, während größere Exemplare 55 und 89 Spiralen haben. Zählen Sie selbst. Mit einem Mal rücken unsichtbare Strukturen unserer Alltagswelt – Verbindungen zwischen vermeintlich unterschiedlichen Objekten – in den Brennpunkt.
Um die verborgenen Details ans Tageslicht zu bringen, genügt es manchmal schon, Dinge und Angelegenheiten etwas genauer unter die Lupe zu nehmen und mit der Quantifizierung unserer Beobachtungen den letzten Schliff anzubringen. Normalerweise betrachten wir die Welt eher verschwommen, doch sobald wir unsere Augen und unseren Verstand den Details öffnen und den Blick für Muster entwickeln, erkennen wir die Welt in ihrer prachtvollen Vielfalt und können die Dinge in einen schärferen Brennpunkt rücken.
Künstliche Blumen züchten
Warum sind so viele in der Natur vorkommende Spiralen auf diese Zahlenfolge abgestimmt? Weder Mathematiker noch Biologen haben dafür eine überzeugende Erklärung. Es ist bekannt, dass die winzigen Einzelblüten, aus denen die Spirale besteht und die wir gezählt haben – beispielsweise die gelben Knospen des Gänseblümchens – vom Mittelpunkt aus wachsen. Wenn neue Knospen entstehen, bewegen sich die älteren auf den runden Rand der Blume zu. Durch diesen Wachstumsprozess wird in dem Moment, wenn die jüngeren, kleinen Blüten die Szene betreten, jede einzelne Knospe an den Rand geschoben.
Eine Theorie behauptet, dass diese Einzelblüten, diese kleinen, jungen Knospen, sich wie Menschen benehmen – sie möchten so viel Spielraum um sich herum haben wie nur möglich. Aber sosehr sie auch ihre Ellbogen einsetzen, um sich Luft zu verschaffen, wird die Mehrzahl der Knospen natürlich wie Sardinen in einer kreisförmigen Büchse zusammengequetscht worden sein, wenn die Blume ihre volle Größe erreicht haben wird. Wissenschaftler haben dieses Verhalten in Computermodellen statt in Sardinenbüchsen simuliert. Das heißt, sie gingen von der Annahme aus, dass diese kleinen Einzelblüten vom Zentrum eines kleinen Kreises aus ihr Wachstum beginnen und sich so positionieren, dass sie so viel Raum wie möglich um sich herum haben.
Sobald der Verdichtungsprozess abgeschlossen ist, erzeugen die Computermodelle, genau wie die Blumen in der Natur, Bilder, die aus paarweise angeordneten Spiralen bestehen, bei deren Abzählung man auf zwei angrenzende Zahlen innerhalb der bekannten Zahlenfolge kommt. Diese Computersimulationen erklären zwar nicht, warum die Spiralen in dieser Form auftreten, sie weisen jedoch darauf hin, dass der entscheidende Faktor des Phänomens die Raummaximierung jeder Einzelblüte ist.
Fortpflanzungsgewohnheiten von Kaninchen
Wir lassen nun die Natur hinter uns, wenden uns wieder der Mathematik zu und stellen fest, dass diese Zahlen nach dem Mathematiker Leonardo de Pisa, der auch als Fibonacci bekannt ist, Fibonacci-Zahlen genannt werden. Leonardo war ein Mitglied der Familie Bonacci und gab sich den Spitznamen Bigallo, was entweder weitgereister Mann heißen kann oder auch Taugenichts. Nachgewiesenermaßen war Fibonacci ein weit gereister Mann und fasziniert von mathematischen Fragen, die anscheinend keinen praktischen Wert hatten – deshalb wollen wir es Ihnen überlassen, wie Sie den Spitznamen Fibonacci interpretieren wollen.
Im Jahr 1202 schrieb Fibonacci eine Abhandlung über Arithmetik und Algebra mit dem Titel Liber abaci. Darin stellte er folgende Frage: Ein gewisser Herr setzte ein Kaninchenpaar an einen Ort, der rundum von einem Zaun umgeben war. Wie viele Kaninchenpaare kann dieses Paar innerhalb eines Jahres zeugen, vorausgesetzt, dass jedes Paar alle vier Wochen ein neues Paar zeugt, das vom zweiten Lebensmonat an fortpflanzungsfähig ist?
Sehen wir uns sein Kaninchengenerationenrätsel an. Wir stellen fest, dass erstens angenommen wird, jedes Paar bestehe aus einem weiblichen und einem männlichen Tier, dass sie sich zweitens nach ihrem ersten Monat plus einem Monat Trächtigkeit fortgepflanzt haben, dass sie drittens jeden Monat in schönster Regelmäßigkeit ein neues Häschenpaar in die Welt setzen und dass sie schließlich monogam sind – Sie erinnern sich sicher an das alte Sprichwort: Im Kaninchenbau gibt es keine Bigamisten.
Wir fangen also zu Beginn des ersten Monats mit einem Paar Kaninchenbabys an (wenn wir von einem Monat sprechen, denken wir immer an den Anfang des Monats). Einen Monat später sind die beiden Babys erwachsene Kaninchen geworden, und im Monat darauf bringen sie ihr erstes Paar Nachwuchshasen zur Welt.
Also haben wir im ersten Monat ein Paar Kaninchen, im zweiten Monat sind es immer noch zwei, jetzt aber sind sie so weit, im Heu zu rammeln – Wenn’s rappelt im Karton, klopf lieber nicht an. Im dritten Monat sehen wir das ursprüngliche Paar, inzwischen stolze Eltern eines neuen Babypaars.
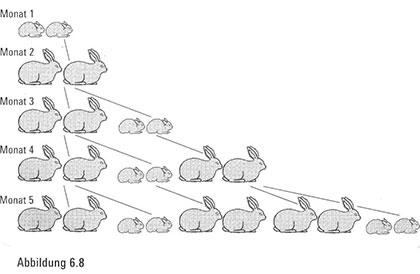
Im vierten Monat bringt das erste Paar erneut ein Pärchen zur Welt, während das erste Nachwuchspaar erwachsen wird – also haben wir drei Paare. Im fünften Monat produziert das erste Paar wieder ein neues Babypaar, während gleichzeitig das erste Nachwuchspaar reif genug ist, um sich fortzupflanzen (was sie auch tun). Das zweite Nachwuchspaar wird lediglich erwachsen. Jetzt haben wir insgesamt fünf Paare. Wenn wir nun – oder viel wichtiger natürlich, die Kaninchen – den Prozess sorgfältig ohne rechtzeitiges oder vorzeitiges Ableben weiterführen, würden sie den in Abbildung 6.8 gezeigten Familienstammbaum hervorbringen.
Überraschung … Hier liegt wieder die Fibonacci-Folge vor. Dieses Rätsel über die Fortpflanzung von Kaninchen ist das erste aufgezeichnete Beispiel, in dem diese Zahlen auftauchen, und deshalb werden sie nach Fibonacci benannt. Aber selbstverständlich war die Natur uns allen voraus, da sie diese wunderbare Sequenz längst in ihre Spiralen verschlüsselt hatte, als Fibonacci im 13. Jahrhundert seine Frage nach den rammelnden Kaninchen stellte. Der Gedanke ist erfrischend, dass die Menschheit letztlich die Natur ein-holen oder zumindest allmählich zu ihr aufschließen kann, wenn wir nur lange genug warten können. Aber vielleicht sollten wir der Natur ihren gebührenden Anteil zollen und die Fibonacci-Zahlen umbenennen in Zahlen der Natur.
Als Postskriptum überlassen wir es Ihnen, Fibonaccis ursprüngliche Frage zu beantworten und zu bestimmen, wie viele Kaninchen nach einem Jahr herumhoppeln werden. Wir wollen nur darauf hinweisen, dass das umzäunte Gelände groß genug sein sollte. Außerdem sollten Sie – falls man Ihnen die Wahl lässt – lieber freiwillig das Füttern übernehmen statt anschließend das Ausmisten.
Fortpflanzungszahlen
Da wir gerade von den Fortpflanzungsgewohnheiten der Kaninchen gesprochen haben, wollen wir auf die Fortpflanzungsgewohnheiten von Fibonacci-Zahlen zurückkommen. Natürlich werden die Fibonacci-Zahlen immer größer, je länger die Liste wird. Aber wie schnell wachsen sie eigentlich an? Nehmen wir an, die Natur bietet uns die Zahlenliste jener Paare an, die vom Abzählen der Spiralen abstrahiert werden, dann liegt es auf der Hand, das Verhältnis von jedem Paar fortlaufender Zahlen auf unserer Liste aufzustellen. Diese Brüche und ihre Entsprechungen in Dezimalzahlen geben uns eine Vorstellung davon, wie schnell die Fibonacci-Zahlen wachsen (Abbildung 6.9).
| Verhältnis aufeinander | Entsprechende | |
| folgender Fibonacci-Zahlen | Dezimalzahlen | |
| 1
1 |
= | 1,0 |
| 2 | ||
| T | = | 2,0 |
| 3 | ||
| 2 | = | 1,5 |
| 5
3 |
= | 1.666… |
| 8 | ||
| 5 | 1,6 | |
| 13 | ||
| 8 | 1,625 | |
| 21 | ||
| 13 | – | 1,6153… |
| 34 | ||
| 21 | = | 1,6190… |
| 55 | ||
| 34 | = | 1,6176… |
| 89 | ||
| 55 | = | 1,6181… |
| 144 | ||
| — | 1,6179 | |
| 89 |
Abbildung 6.9
Das Bemerkenswerte beim Betrachten der Liste, die die Verhältnisse aufeinanderfolgender Fibonacci-Zahlen dokumentiert, liegt in der Tatsache, dass die entsprechenden Dezimalwerte sich einem bestimmten Wert annähern. Diese Zahlen bewegen sich immer näher auf die Zahl 1,61803 soundso viel zu, eine Zahl, die im Augenblick nicht besonders anziehend oder natürlich erscheint. Aber vielleicht haben wir sie noch nicht ins rechte Licht gerückt.
Das Rätsel des Fläschenparadoxonis. Das am Anfang des Kapitels besprochene Paradoxon eröffnet uns eine visuelle Möglichkeit der Bestätigung, dass jene aufeinanderfolgenden Quotienten sich in der Tat einem festgelegten Wert annähern. Falls Sie das Rätsel gelöst haben sollten, haben Sie festgestellt, dass ein Quadrat von 8×8 Einheiten und daher mit einer Fläche von 64 Einheiten in Stücke geschnitten und zu einem Gebilde neu arrangiert werden konnte, das ein Rechteck von 5X13 und mit einer Fläche von 65 Einheiten zu sein schien. Sie haben also die paradoxe Erfahrung gemacht, dass Sie durch das Verschieben der Puzzleteile die Fläche vergrößern konnten! Wenn dieses Phänomen tatsächlich real wäre, dann wäre der nächste Schritt sonnenklar: Sie kaufen ein kleines Grundstück – 30 mal 30 Zentimeter – auf Hawaii und verschieben Stücke davon so lange, bis Sie die ganze Insel besitzen – keine schlechte Investition. Natürlich vermitteln uns gesunder Menschenverstand und Mathematik, dass Flächen sich nicht derart ausdehnen können. Sie könnten unseren Vorschlag nicht wirklich in die Tat umsetzen. Was lief also falsch bei der Umwandlung vom Quadrat ins Rechteck?
Wenn wir das Bild des Rechtecks, das Sie erhielten (Abbildung 6.10), sorgfältig betrachten, erkennen wir, dass es eine fast unsichtbare Lücke entlang der Diagonalen gibt.
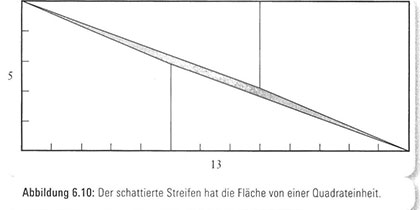
Diese schmale Lücke ist die zusätzliche Flächeneinheit, die wir anscheinend dazugewonnen haben. Ziehen wir unsere Zahlenliste zurate, stellen wir fest, dass 5, 8 und 13 – die Zahlen, die wir für die Ausmaße des Quadrats und Rechtecks benutzt haben – drei aufeinanderfolgende Fibonacci-Zahlen sind. Beachten Sie, dass 8X8 und 5X13 sich um 1 unterscheiden. Es stellt sich heraus, dass es sich hier um ein Muster handelt: Für beliebige drei aufeinanderfolgende Fibonacci-Zahlen wird die mittlere, mit sich selbst multiplizierte Zahl stets um 1 vom Produkt der beiden flankierenden Zahlen abweichen. Bitte betrachten Sie als neue Veranschaulichung den Fibonacci-Dreier 89, 144, 233. Multiplizieren Sie die mittlere Zahl 144 mit sich selbst und vergleichen Sie den Betrag mit dem Produkt von 89 und 233:
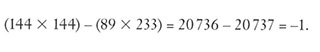
Wenn wir ein paar Divisionen durchführen, können wir diese Beobachtung auf eine mathematisch etwas geschicktere Art und Weise ausdrücken. Vom Standpunkt der quadratischen und rechteckigen Dimensionen 5, 8 und 13 betrachtet, sehen wir, dass
![]()
Allgemeiner formuliert, trifft angesichts dreier aufeinanderfolgender Fibonacci-Zahlen das folgende schöne Verhältnis immer zu:
![]()
Diese Beobachtung impliziert, dass bei der Zunahme der Fibonacci-Zahlen der Abstand zwischen zwei aufeinanderfolgenden Brüchen aus unserer Tabelle )Abbildung 6.9) immer weiter abnimmt und sich auf null zubewegt. Aber welchem Wert nähern sich jene Verhältnisse der in der Natur vorkommenden Spiralen? Die Dezimalzahl 1,61803 soundso viel scheint als Zielwert äußerst willkürlich zu sein. Wir stellen jedoch fest, dass diese Zahl genauso schön ist wie die Spiralen, die uns zu ihr führten. Um dieser Behauptung gerecht zu werden, müssen wir uns der Zahl aus der angemessenen Richtung nähern.
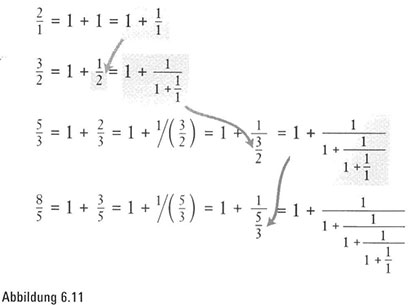
Einsen über einsen. Wir können die Brüche aus unserer Tabelle so ausschreiben, dass jeder Bruch zu dem Bruch darüber in Beziehung gesetzt wird. Fangen wir also mit einem beliebigen Bruch auf unserer Liste an, so können uns wiederholte Divisionen an die Spitze der Tabelle bringen (Abbildung 6.11). Das heißt, wir können jeden beliebigen Bruch als Kettenbruch ausdrücken, nämlich als einen Bruch in einem Bruch in einem Bruch und so weiter. Oder wir wählen die Aussage 1 plus 1 über 1 plus 1 über x plus 1 über 1 …, bis wir bei der letzten i angelangt sind (Abbildung 6.12). Eigentlich erhalten wir jeden aufeinanderfolgenden Bruch in unserer Tabelle aus dem vorangegangenen, wenn wir die letzte 1 durch 1 +1/1rsetzen.
Das Zusammenwirken von Natur und Zahl – Lotto und Glücksspiele Tipps Teil 2


