Das Taxieren von Zahlen und ihre Bedeutung bei den Glücksspielen Teil 2

Das Taxieren von Zahlen und ihre Bedeutung bei den Glücksspielen Teil 1

Sechs Trennungsgrade
Numerisches Denken kann uns unseren Lieblingshelden und -heldinnen näher bringen. Haben Sie sich nicht schon einmal gewünscht, Sie könnten Franklin D. Roosevelt, Margaret Thatcher, Marylin Monroe oder Elvis die Hand schütteln? Obwohl wir nicht jeden Prominenten unserer Wahl kennenlernen können- vor allem nicht jene, die vor unserer Geburt gestorben sind -, sind wir dem Ruhm näher, als wir ursprünglich geglaubt haben mögen. Sie sind nämlich mit ziemlicher Sicherheit weniger als sechs Handschläge entfernt von Roosevelt, Thatcher, Marylin und Elvis.

Das heißt, Sie haben jemandem die Hände geschüttelt (ein Handschlag von Ihnen entfernt), der die Hände von jemandem geschüttelt hat (zwei Handschläge von Ihnen entfernt), der die Hände von wieder jemand anderem geschüttelt hat (drei Handschläge), der die Hände von jemandem geschüttelt hat (vier), der die Hände von jemandem geschüttelt hat (fünf), der Elvis die Hände geschüttelt hat (sechs). Sie sind also Elvis so nahe, dass Sie wahrscheinlich fühlen, wie Ihre Hüften rotieren, während Sie genau diesen Satz hier lesen. Die Welt ist definitiv kleiner, als wir uns das vorstellen können.

Wie kann es wahr sein, dass wir alle so eng miteinander verbunden sind? Fangen wir einfach mit einer berühmten Persönlichkeit wie Roosevelt an. Im Laufe seines Lebens in der Öffentlichkeit schüttelte er vielen politisch aktiven Menschen die Hände. Dazu gehörten auch alle Mitglieder des Kongresses, die Gouverneure aller Staaten, die militärischen Führer, die herausragenden amerikanischen Regierungsmitglieder und die Regierungschefs in aller Welt. Hinzu kommen noch Tausende normaler Bürger. Diese Menschen schüttelten die Hände anderer Politiker, die ihrerseits die Hände mit politisch aktiven Bürgern und religiösen Führern schüttelten. Diese Leute wiederum schüttelten ihren Gemeindemitgliedern und damit indirekt auch deren Nachbarn die Hände. Mittlerweile ist fast jeder beteiligt. Nachdem nun alle noch ihren Cousins und Schwägern die Hände geschüttelt haben, hat im Wesentlichen jedermann indirekt Franklin D. Roosevelt die Hände geschüttelt.

Sie selbst können Ihren eigenen Handschlagtrennungsgrad von jedem anderen Menschen schätzen. Nehmen wir an, Sie möchten Ihre Handschlagdistanz zu dem Schauspieler Kevin Bacon schätzen. Sie könnten zunächst darüber nachdenken, welches die berühmteste Person ist, der Sie je die Hände geschüttelt haben. Oder Sie kennen vielleicht jemanden, der einmal einem Prominenten begegnet ist. Berühmte Schauspieler und berühmte Menschen im Allgemeinen haben sich entweder gegenseitig die Hände geschüttelt oder sind nur einen Handschlag voneinander entfernt. Lind so ist es denn auch wahrscheinlich, dass nur drei Handschläge erforderlich sind, um zu einer berühmten Person zu gelangen, und man mit drei weiteren Handschlägen mit jeder beliebigen anderen Person in Berührung kommt. Vielleicht braucht man noch ein paar mehr Handschläge, um einen Menschen zu erreichen, der in einer abgelegenen Region Chinas lebt.

Mit nicht allzu vielen zusätzlichen Handschlägen können wir sogar mit den Gründungsvätern der US A in Verbindung treten. Nehmen wir zum Beispiel Thomas Jefferson. Er starb am 4. Juli 1826, am 50. Jahrestag der Unterzeichnung der Unabhängigkeitserklärung. Er hat mit Sicherheit etlichen Leuten die Hand geschüttelt, die bis ins 20. Jahrhundert hinein gelebt haben. Und unter diesen damals Achtzig- oder Neunzigjährigen könnte jemand die Hand eines Kleinkinds geschüttelt haben, das heute noch lebt. So könnte es durchaus möglich sein, dass Sie nur durch sechs oder sieben Handschläge, mit ziemlicher Sicherheit aber durch acht oder neun Handschläge von Thomas Jefferson getrennt sind. Tatsächlich gibt es heute lebende Personen, die möglicherweise jemandes Hände geschüttelt haben, der Thomas Jefferson die Hände geschüttelt hat. Die Welt ist wahrhaftig ein globales Dorf. Wein würden Sie gern begegnen? Er oder sie ist nur ein paar Handschläge entfernt von Ihnen.

Die weniger erfreuliche Seite dieser Beobachtung läuft darauf hinaus, dass wir nur sieben oder acht Handschläge von den abstoßendsten oder mit den ansteckendsten Krankheiten behafteten Menschen des Planeten entfernt sind. Wir können nur hoffen, dass sich ein paar der Handschüttler in der Kette, die zu uns führt, auch gründlich die Hände gewaschen haben. Wollen wir nun die Diskussion auf einem etwas ernsthafteren Niveau weiterführen, dann ist die Tatsache, dass wir alle so eng miteinander verbunden sind, auch der Grund, weshalb ansteckende Krankheiten potenziell so verheerend sind. Angenommen, es gäbe eine tödliche Krankheit, bei der über einen bestimmten Zeitraum hinweg keine Symptome auftreten und die durch die Atemluft oder durch Händeschütteln übertragbar wäre. Dann würde diese Krankheit schnell nahezu jeden Menschen auf dem Planeten infizieren. Es ist schon ziemlich ernüchternd, wenn man erkennt, dass wir uns inzwischen alle infiziert hätten, wenn HIV durch die Luft übertragbar wäre.

Wir sitzen auf unserem Kartenspiel
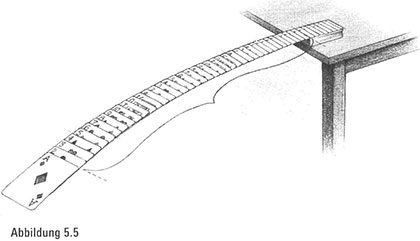
Lassen wir nun unseren überbevölkerten Planeten und seine menschlichen Netzwerke hinter uns, und setzen wir uns mit einem Kartenspiel ganz allein an einen Tisch. Stellen wir uns vor, wir legen einen sehr großen Stapel Spielkarten auf einen Tisch und arrangieren sie äußerst sorgfältig, sodass die obersten Karten immer weiter über die Tischkante hinausragen (Abbildung 5.5). Natürlich dürfen wir, wie bei keinem Kartenspiel,

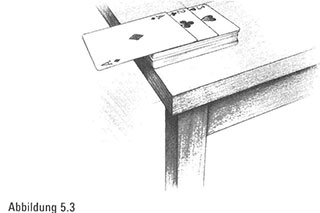
Klebstoff oder irgendeine andere Methode zur Befestigung der Karten benutzen. Wie weit kann der Kartenstapel über den Tisch hinausragen, wenn wir von unbegrenztem Kartennachschub ausgehen können? Es geht vor allem um Folgendes:

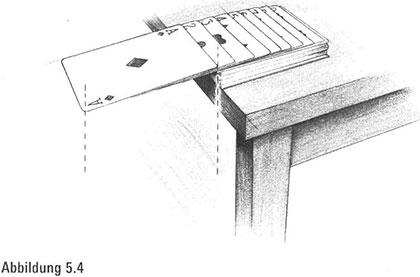
1. Können wir die Karten so verschieben, dass die oberste Karte über die Tischkante hinausragt (Abbildung 5.4)?
2. Können wir die Karten so arrangieren, dass die oberste Karte mehr als 60 Zentimeter über die Tischkante hinausragt (Abbildung 5.5)?
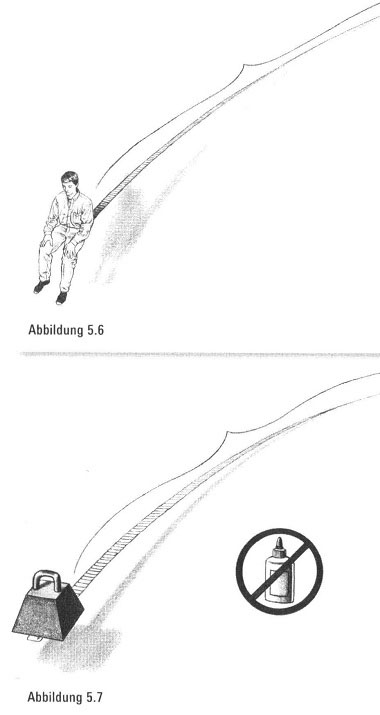
3. Können wir, ohne auch hier Klebstoff verwenden zu müssen, die Karten so verschieben, dass die oberste Karte mehr als eineinhalb Kilometer über die Tischkante hinausragt und obendrein alles so arrangiert ist, dass wir auf der obersten Karte sitzen können, ohne dass der Stapel darunter zusammenbricht (Abbildung 5.6)?

Überraschung. Die Antworten lauten ja, ja und ja! Es ist tatsächlich so: Wenn wir genügend Karten zur Verfügung haben, können wir sie theoretisch so stapeln, dass sie so weit über den Tisch hinausragen können, wie wir wollen. Obendrein können wir ein im Voraus festgelegtes, beliebiges Gewicht auf die oberste Karte – die am weitesten vom Tisch entfernt ist – platzieren, ohne dass das nicht festgeklebte Kartenspiel umkippt (Abbildung 5.7). Diese Tatsache widerspricht völlig unserer Intuition. Natürlich hantieren wir dabei in einer hypothetischen Welt, in der wir uns einen Stapel von einer Billion Karten oder mehr vorstellen. Außerdem nehmen wir dabei an, dass dieser unrealistisch hohe Stapel denselben physikalischen Gesetzen gehorcht wie der normale Stapel von 52 Karten. Kein echter Tisch könnte das Gewicht eines solchen Kartenstapels aushalten, aber trotzdem können wir beschreiben, was passierte, wenn der Tisch unwahrscheinlich tragfähig wäre und es unwahrscheinlich viele Karten gäbe. Aber wie ist diese Bravourleistung möglich? Und wie viele Karten würden wir brauchen?

Die folgende Erklärung enthält ein paar numerische Berechnungen, die vielleicht nicht jedermanns Sache sind. Wir bitten daher alle Leser, die an den technischen Details nicht interessiert sind, den Text nur flüchtig zu lesen oder lediglich die Bilder zu betrachten und mit dem nächsten Kapitel anzufangen. Wir können also ohne Hilfe von Klebstoff Spielkarten fächerförmig so ausbreiten, dass sie weit über die Tischkante hinausragen, und uns dann auf die am weitesten entfernte Karte setzen, ohne dass der Stapel umfällt. An dieser unglaublichen Tatsache können wir uns alle erfreuen – auch diejenigen, die nicht haargenau die Details erfahren möchten, wie das wohl möglich ist.

Wir fangen oben an. Statt uns auf das untere Ende des Stapels zu konzentrieren und uns nach oben vorzuarbeiten, sehen wir uns die Spitze des Stapels an und arbeiten uns nach unten. Die entscheidende Idee dabei ist folgende: Damit die oberste Karte nicht herunterfällt, muss ihr Gravitationszentrum auf einem bestimmten Punkt der Karte ruhen, die unmittelbar unter ihr liegt. Das Gravitationszentrum eines Objekts ist jener Punkt, auf dem das Objekt perfekt ausbalanciert wäre, wenn man es auf eine Nadelspitze setzte. Befände sich das Gravitationszentrum der obersten Karte nicht über der darunterliegenden Karte, würde die oberste Karte herunterfallen (Abbildung 5.8).

Es fällt nicht schwer, herauszufinden, wie weit die oberste Karte im Verhältnis zu der unter ihr liegenden Karte herausragen darf. Wenn mehr als die Hälfte über die untere Karte hinaushängt, fällt sie selbstverständlich herunter. Also werden wir versuchen, die Karten so weit wie möglich hinausragen zu lassen, um zu sehen, wie sich das Gravitationszentrum der Karten mit jeder weiteren (darunterliegenden) Karte verschiebt.

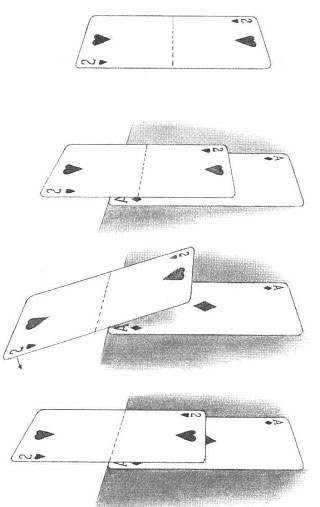
Abbildung 5.8: Befindet sich das Gravitationszentrum über der darunterliegenden Karte, bleibt die oberste Karte liegen. Befindet sich das Gravitationszentrum nicht über J der unteren Karte, fällt die Karte herunter. Befindet sich das Gravitationszentrum am j Rand der unteren Karte, befindet sich die oberste Karte im perfekten Gleichgewicht und bleibt dort liegen.

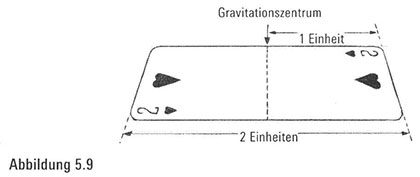
Nehmen wir an, jede Karte hätte eine Länge, die zwei Einheiten entspricht. Dann befindet sich das Gravitationszentrum der obersten Karte auf deren halber Länge – eine Einheit vom Kartenrand entfernt (Abbildung 5.9).

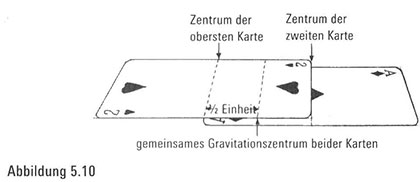
Wenn wir die nächste Karte darunterlegen, sodass ihr linker Rand direkt unter dem Gravitationszentrum der ersten Karte liegt (Ab- bildung io), dann liegt das gemeinsame Gravitationszentrum der beiden Karten ½ Einheit links vom Zentrum der zweiten Karte, da das Gravitationszentrum der zweiten Karte eine Einheit jenseits des Gravitationszentrums der ersten Karte liegt.

In Wirklichkeit
entspricht das gemeinsame Gravitationszentrum beider Karten dem Durchschnitt der Gravitationszentren jeder einzelnen Karte.

Jetzt wollen wir eine dritte Karte darunter platzieren, sodass ihr linker Rand sich genau unter dem gemeinsamen Gravitationszentrum der beiden obersten Karten befindet (Abbildung 5.11). Um das

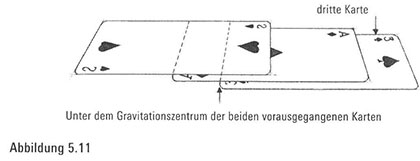
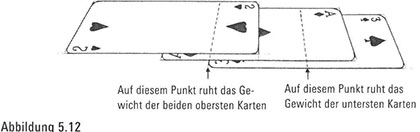
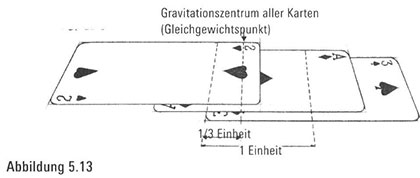
Gravitationszentrum aller drei Karten zu bestimmen, führen wir folgende Rechnung durch: Wir wissen, dass sich das Gravitationszentrum der beiden obersten Karten genau am linken Rand der dritten Karte befindet und das Gravitationszentrum der dritten Karte natürlich eine Einheit von seinem eigenen linken Rand entfernt ist. Also haben wir zwei Kartengewichte am linken Rand der dritten Karte und ein Kartengewicht um eine Einheit nach rechts verschoben (Abbildung 5.12). Deshalb berechnen wir, gemessen vom linken Rand der dritten Karte, den Durchschnittswert und
stellen fest, dass sich das Gravitationszentrum (2X0+ 1)/3, Einheiten rechts vom linken Ende der dritten Karte befindet (Abbildung 5.25).

Betrachten wir nun die Lage der vierten Karte von oben. Wir wollen sie so hinlegen, dass die obersten drei Karten gerade noch so auf ihrem linken Rand im Gleichgewicht sind. Das heißt, das Gravitationszentrum der obersten drei Karten wird sich genau über dem linken Rand der vierten Karte befinden. Dann wird sich das neue Gravitationszentrum aller vier Karten (3X0+ 1)/4 Einheiten rechts vom linken Rand der vierten Karte befinden (Abbildung 5.24). Langsam zeigt sich ein Muster. Es wird deutlich, dass, sobald wir zum Beispiel 100 Karten ausgelegt haben, wir die 101.

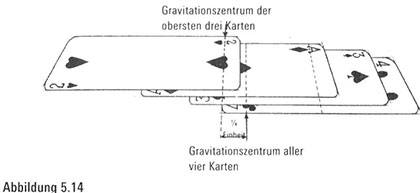
Karte so unter die anderen schieben können, dass sich ihr linker Rand genau unter deren Gravitationszentrum befindet, sodass die 100 Karten darüber nicht herunterfallen werden. Das neue Gravitationszentrum der 101 Karten befindet sich (100 X 0 + 1)/101 Einheiten rechts vom linken Ende der 101. Karte.

Setzen wir das Ganze fort und platzieren das Gravitationszentrum des gesamten Kartenspiels über dem Tisch, wird der Stapel nicht umfallen. Wenn wir also wissen wollen, wie weit ein Stapel von vier Karten über den Tisch hinausragen darf, müssten wir wissen, wie weit das Gravitationszentrum dieser vier Karten vom linken Ende der obersten Karte entfernt sein darf (Abbildung 5.15). Wir erkennen, dass die Antwort folgendermaßen lautet:

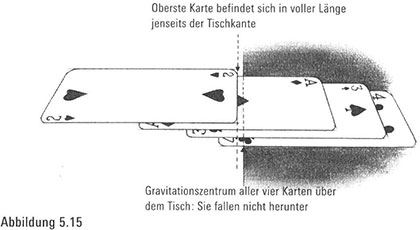
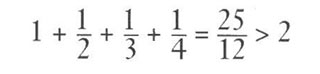
Da die Länge der Karten 2 Einheiten beträgt, zeigt uns diese Rechnung, dass der linke Rand der obersten Karte mehr als 2 Einheiten über die Tischkante hinausragt und daher die oberste Karte sich in voller Länge jenseits der Tischplatte befindet. Suchen Sie sich vier Spielkarten und versuchen Sie es! Wenn Sie sorgfältig zur Sache gehen, können Sie tatsächlich diesen erstaunlichen Anblick genießen.

Wir wollen uns nun mit der anderen Frage beschäftigen. Lassen sich die Karten so stapeln, dass die oberste Karte weiter als rund 60 Zentimeter, drei Meter oder gar mehr als einen Kilometer über die Tischkante hinausragt? Die Antwort lautet in allen drei Fällen ja, denn wenn wir genügend Karten einsetzen, können wir das Gravitationszentrum des gesamten Stapels beliebig weit rechts von der obersten Karte platzieren.

Angenommen, wir wollen ohne die Verwendung von Klebstoff einen Kartenstapel errichten, dessen oberste Karte mehr als eineinhalb Kilometer über die Tischkante hinausragt. Dafür brauchten wir zwar eine Menge Karten, aber theoretisch ist so ein Stapel durchaus möglich. Die Umsetzung lässt sich am einfachsten anhand von Karteneinheiten demonstrieren, weshalb wir zunächst eine Meile in Kartenlängen ausdrücken wollen. Wenn, wie wir zuvor festgelegt haben, eine Karte zwei Einheiten sind, dann entspricht eine Meile – ca. 1,6 Kilometer oder 5280 Fuß oder etwa 60000 Zoll – etwa 40000 unserer Karteneinheiten (bei der Annahme, dass die Karten ungefähr 3 Zoll lang sind).

Wir wollen nachweisen, dass wir die Karten so ausbalancieren könnten, dass die oberste Karte eine Meile oder rund eineinhalb Kilometer – das sind ungefähr 40000 unserer Karteneinheiten- über die Tischkante hinausragt. Bei vier Karten entspricht der Abstand zwischen dem linken Rand der obersten Karte und der Tischkante der Summe der Kehrwerte der ersten vier natürlichen Zahlen. Dieses Muster setzt sich fort. Wenn wir also 100 Karten haben, dann beträgt der Abstand von der Tischkante zum linken Rand der obersten Karte was annähernd 5,2 Karteneinheiten entspricht.

Nebenbei bemerkt, stellen wir fest, dass wir mit zwei regulären Kartenspielen den äußersten Rand der obersten Karte mehr als zweieinhalb Kartenlängen über die Tischkante hinausragen lassen könnten!

Jetzt kristallisiert sich unser Auftrag heraus: Wir wollen herausfinden, wie viele Karten wir für die Summe aller Kehrwerte bis zu der Zahl brauchen, die 40000 übersteigt. Um das komplizierte Summieren ein wenig handhabbarer zu machen, stellen wir die Brüche so zusammen, dass ihre Summe jeweils mindestens ½ ergibt. Wenn wir dann 80000 Halbe gefunden haben, hätten wir die Gesamtsumme, die – wie gewünscht – 40000 übersteigt. Wir wollen uns nun ansehen, wie dieses Gruppierungsverfahren aussehen könnte:

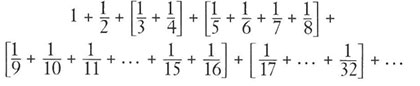
Wir behaupten, dass die Summe der Brüche innerhalb jedes Klammerpaars V2 übersteigt. Schauen wir uns also an, warum diese Behauptung für die ersten Klammerpaare gilt. Beginnen wir mit der ersten Klammer:

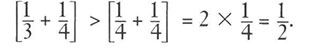
Diese Berechnung entspringt einfach folgender Beobachtung: Wenn zwei ¼ gleich ½ sind, dann erhalten wir bei der Addierung von ¼ und einem Wert, der etwas größer ist als ¼ , mehr als ½ . Die gleiche Logik kann auf die nächste Klammerreihe angewandt werden. Wir stellen fest, dass:

Also summieren sich die vier Terme von 1/5 bis 1/8 wieder auf mehr als ½ . In ähnlicher Weise ergibt die Summe der acht Terme von 1/9 bis 1/16 mehr als ½ . Die Addition der nächsten 16 Terme (von 1/17 bis zu 1/32) ergibt ebenfalls mehr als ½ , und auch die nächsten 32 Terme (von 1/33 bis 1/64) summieren sich auf mehr als ½ und so weiter ad infinitum.

Wenn wir daher die oberste Karte eine Meile über die Tischkante hinausragen lassen möchten, müssten wir genügend Karten haben, damit die Summe der Brüche größer als 40000 wird. Wie viele Karten müssten wir dafür organisieren? Die Zahl hat ungefähr 17000 Ziffern! Um ein Gefühl für diese Zahl zu bekommen, müssen wir uns vorstellen, dass die Anzahl der Atome im Universum eine 80-stellige Zahl ist. So besteht zwar theoretisch die Möglichkeit, Spielkarten eine Meile über die Tischkante hinausragen zu lassen, aber Sie sollten es nicht zu Hause ausprobieren. Diese 17000-stellige Zahl lässt alle anderen Zahlen in diesem Kapitel winzig erscheinen – sie schießt wirklich den Vogel ab.

Abschließend stellen wir noch fest, dass wir bequem auf dem herausragenden Kartenstapel (wie in Abbildung 5.16) sitzen können. Um herauszufinden, wo wir sitzen können, müssen wir lediglich eine Menge Karten von der Spitze des Stapels entfernen, die insgesamt etwas mehr wiegen als wir selbst, und uns dann auf die verbleibende oberste Karte setzen. Das Gravitationszentrum dieser ausgelegten Karten befindet sich genau am Ende der nächsten Karte, sodass wir sicher ganz gelassen auf dem höchsten Punkt eines sehr hohen Kartenstapels sitzen können – ein Anblick, der unserer Intuition heftig widerspricht.

Zusammenfassung
Zahlen sind wirklich faszinierende Objekte und kommen in allen Formen und Größen vor. Tausende, Millionen, Milliarden, Billionen, Trillionen und selbst Zahlen jenseits dieser Menge können Bedeutung für uns haben. Um ein Verständnis für diese Mengen zu entwickeln, können wir uns Szenarios ausdenken: vom Zählen der Sterne bis zum Stapeln von Karten. Wenn wir uns angewöhnen zu zählen, öffnen wir uns für eine Welt der Genauigkeit und der Detailtreue.