
Das Taxieren von Zahlen und ihre Bedeutung bei den Glücksspielen Teil 1
Wie viele‘? Wie groß‘? Wie schnell‘?
Wo eine Zahl ist, ist auch Schönheit.
Proclus
Offensichtlich … Angenommen, wir falten ein normales Stück Papier in zwei Hälften. Dann falten wir es noch einmal und noch einmal und so weiter. Während das Papier in Wirklichkeit nur etwa siebenmal wiederholt gefaltet werden kann, wollen wir uns nun vorstellen, es ungefähr fünfzigmal zu tun. Wie dick ist das gefaltete Papier, wenn wir fertig sind? Zwei Zentimeter, einen halben Meter, einen Meter?
Überraschung … Das in Ihrer Vorstellung gefaltete Papier wäre ein Turm, der über 160000000 Kilometer (ja, das sind einhundertsechzig Millionen Kilometer) ins Weltall hinein- und über die Sonne hinausragen würde. Nicht schlecht für fünfzig Faltungen …
Zahlen
Die meisten von uns denken an Zahlen, wenn sie an Mathematik denken. Und wenn wir an Zahlen denken, denken wir ans Zählen. Während wir zwar den Akt des Abzählens auf den ersten Blick als nicht grundlegend betrachten, gehört er doch gewiss zu den Dingen, auf die wir zählen können. (Pardon.) Im Gegensatz zu unserem ursprünglichen Eindruck hat der Abzählvorgang ein Potenzial, das weit über seine scheinbare Einfachheit hinausgeht. Es gibt nur wenige abstrakte Vorstellungen in der Geschichte der Menschheit, die uns mit vergleichbaren Fähigkeiten ausgestattet haben, die Welt nuancierter zu betrachten. Wenn man die Bedeutung von wie viele erkennt, kommt das einem Blick durch ein Mikroskop gleich – plötzlich sehen wir eine detailreichere Welt. In diesem Kapitel werden wir entdecken, dass der einfache Akt des Zählens den Schlüssel für viele überraschende Resultate bereithält.
Es gibt drei Arten von Menschen: die, die genau zählen, und die, die nicht genau zählen. Natürlich hängt in der rauen Wirklichkeit das, was als Zählen durchgeht, von der jeweiligen Situation ab – manchmal fühlen wir uns gezwungen, sorgfältig zu zählen, während bei anderen Gelegenheiten eine grobe Schätzung genügen wird. So neigen wir beispielsweise dazu, genau zu zählen, wenn wir den Flughafen verlassen und sichergehen wollen, dass wir alle Koffer und Kinder im Schlepptau haben. Allerdings verzichten wir auf genaues Zählen und halten uns eher an Größenordnungen, wenn es um die roten Zahlen der Staatsschulden oder um die schwarzen Zahlen von Bill Gates geht – das heißt, wir achten zwar auf die Anzahl der Nullen, die am Ende der Zahl stehen (sagen wir, zehn Milliarden oder hundert Milliarden), aber wir kümmern uns kaum darum, ob die Zahl, die den Nullen vorausgeht, eine i oder eine 2 ist (10 Milliarden oder 20 Milliarden). Wie sich herausstellt, können beide Zählweisen – sowohl die genaue als auch die geschätzte Größenordnung – dazu beitragen, unsere Sicht der Dinge zu erweitern.
Ein bekanntes Beispiel, wie Zahlen eine Menge genauestens messen oder schätzen, ist das Alter. Über einen Zeitraum von mehr als 40 Jahren schätzte der gefeierte Komiker Jack Benny sein Alter auf 39 Jahre- ein Klassiker der Komikergeschichte, aber nicht unbedingt die genaueste Schätzung der Menschheitsgeschichte. Einige Jahre vor Bennys Geburt kam die Erde zur Welt; und im 17. Jahrhundert errechnete Bischof James Ussher sogar auf den Tag genau den Geburtstag der Erde: Am 23. Oktober 4004 v. Chr. Diese faszinierende Genauigkeit er-reichte er durch Anwendung astronomischen Wissens und biblischer Geschichte. So konnte er durch alle aufgezeichneten Zeugungen zurückreisen, bis er bei Adam und Eva angekommen war. Allerdings wurde Usshers Vision einer recht jugendlichen Erde (mit ihren knapp 6000 Jahren) vom Zahn der Zeit der Garaus gemacht. Im 19. Jahrhundert setzte der Geologe Charles Lyell wissenschaftliche Beweise ein, um die Erde genauer zu kartieren, und legte ihr Alter auf viele Millionen Jahre fest. Dank Dr. Lyell kam die Erde seitdem bei Kinobesuchen in den Genuss eines Preisnachlasses für Senioren.
Heute glauben Wissenschaftler, die Erde sei ein paar Milliarden Jahre alt, und ihre modernen Messverfahren sind aller Wahrscheinlichkeit nach kaum radikal falsch zu nennen – obwohl Bischof Ussher im 17. Jahrhundert natürlich das Gleiche von seiner eigenen Methode geglaubt haben mag. Wenn wir das Alter der Erde auf ein paar Millionen beziehungsweise Milliarden Jahre schätzen, ist unsere Vorstellung von der Welt grundlegend anders als bei der Annahme, sie sei nur ein paar tausend Jahre jung. So bekommen bei der Voraussetzung eines fortgeschrittenen Alters der Erde beispielsweise die natürlichen Phänomene – vor allem die allmählichen wie Erosion und die seltenen, wie etwa Erdbeben und Vulkane – genügend Zeit, um ihre dramatischen Effekte zu erzeugen: Schluchten, Berge und Kontinente. Deshalb verändert ein Größenordnungskonzept des Erdalters unsere Perspektive, wenn es um die Frage geht, auf welche Einflüsse die häufigen Gesichtsstraffungen der Erde zurückzuführen sind.
Natürliche Zahlen
Natürliche Zahlen sind die numerische Grundlage, auf der unser quantitatives Gespür für Mathematik und für die Welt beruht. Die natürlichen Zahlen sind unsere Zählzahlen – x, 2, 3, 4, 5 und so weiter bis unendlich. Denn natürlich fließt der Strom der natürlichen Zahlen endlos weiter.
Es gibt zwei Arten natürlicher Zahlen: die kleinen und die großen. Wir kennen die kleinen Zahlen und lieben sie, weil wir uns mit ihnen wohlfühlen und sie uns tagtäglich begegnen. Die anderen Zahlen erscheinen uns fremdartig und furchterregend.
Es ist interessant, die Tatsache zu berücksichtigen, dass die meisten natürlichen Zahlen zweifellos riesig sind und deshalb absolut keine Bedeutung für uns haben. In Wirklichkeit ist kein menschliches Wesen, weder unter den Toten noch unter den Lebenden, jemals allen natürlichen Zahlen begegnet. Und hier enthüllen wir eine jungfräuliche Zahl, bis zu ihrem Auftritt in diesem Sportwetten-Portal von noch keinem menschlichen Auge jemals berührt.
Hier ist unsere digitale Debütantin:
50588773485839972782674565498949117196545668765212321 654545497646412141916564654464654564149848949498198949 876313213465462198498198100418098787818009098741596512 02612545004088509987700112 8588907542123500205569868189 6020054567133896549116311664006884640131455047888772325 99524838798255259159871258059885254155859885222699632268
9870465446465456414984894949819694967031321346554621984
9819810041809878781800909874159651202612545004098255259
1598712580598852541558598852226996322689870465446465456 3720960071.
Eigentlich ist dieses numerische Nymphchen einfach nur eine zufällige Aneinanderreihung von 500 Ziffern. Die Wahrscheinlichkeit, dass jemand mit dem Wunsch, eine 500-stellige Zahl niederzuschreiben, zufällig genau den gleichen Wert erzeugt, beträgt 1/10/500. Wie selten ist das? Angenommen, jeder der 6,4 Milliarden Menschen auf der Erde nimmt an einer weltweiten Tombola teil. Einmal pro Woche wird ein Sieger per Zufallslos aus dem riesigen Menschheitspool ermittelt. Es ist wahrscheinlicher, dass Sie diese weltweite Tombola ein ganzes Jahr lang jede Woche gewinnen, als rein zufällig eine 500-stellige Zahl niederzuschreiben, die genau mit der oben gezeigten übereinstimmt.
Natürlich gibt es unendlich viele Zahlen, sodass es eben auch unendlich viele gibt, die noch kein Mensch jemals gesehen hat. Mancher Leser aber mag sich gefragt haben, ob irgendjemand schon einmal bis zu diesem speziellen 500-stelligen Wert gezählt hat. Denn wäre es nicht möglich, dass sich irgendeine ägyptische Gelehrte, vielleicht in der dritten Dynastie, schon einmal bis zu genau dieser Zahl hochgezählt hat? Nein, wirklich nicht. Wir wollen nun sehen, warum nicht.
Die alten Ägypter haben Erstaunliches geleistet. Sie bauten Pyramiden, die angesichts ihrer Technologie unglaublich groß und kompliziert erscheinen, und sogar heute noch ahmen die Tänzer in den Retrotanzclubs beim 1980er-Hit Walk like an Egyptian ihren Gang nach. Dennoch kann kein Mitglied dieser talentierten Gruppe bis zu dieser Zahl gelangt sein. Nehmen wir an, wir versetzten diese ägyptische Gelehrte in noch frühere Zeiten zurücksagen wir, bis zum Augenblick des Urknalls vor rund 13,7 Milliarden Jahren – und rüsteten sie mit einem Supercomputer aus, dessen Zählfähigkeit bei einer Billion Zahlen pro Sekunde läge. Wie nahe wäre nun dieser Supercomputer an unsere 500-stellige Zahl herangekommen, wenn er seit der Geburt des Universums mit Lichtgeschwindigkeit zählte und niemals anhielte?
Es lässt sich leicht schätzen, wie weit unser ägyptischer Supercomputer mit dem Zählen gekommen wäre. Wir multiplizieren einfach die 13,7 Milliarden Jahre mit 365 Tagen pro Jahr, mit 24 Stunden pro Tag, mit 60 Minuten pro Stunde, mit 60 Sekunden pro Minute und mit 1 Billion Zähleinheiten pro Sekunde. Wenn wir diese Mengen miteinander multipliziert haben, erhalten wir eine Zahl mit lediglich 29 Stellen. Diese Zahl ist so winzig im Vergleich zu unserer 500-stelligen Zahl, dass diese Anstrengung noch nicht einmal als ein guter Anfang bewertet werden könnte. Ist es nicht erstaunlich, dass das gesamte Alter des Universums in trillionstel Sekunden mit einer Zahl gemessen werden kann, die weniger als 30 Stellen hat? Eine 500-stellige Zahl bedeutet für die rechnerische Praxis rein gar nichts. Sie ist einfach zu groß.
Numerische Namen
Die Zahlen, über die wir hier sprechen, haben natürlich auch Namen. Aber eigentlich müssen die meisten natürlichen Zahlen erst noch benannt werden. Und diejenigen, die bereits einen Namen haben, sind bloße Staubkörnchen, verglichen mit den meisten natürlichen Zahlen. Vielleicht sollten wir uns ein Beispiel an jenen Firmen nehmen, die für 50 Dollar einen weit entfernten Stern nach einem Ihrer Lieben benennen. Nach diesem Vorbild könnten wir eine Firma gründen, die für ein bescheidenes Honorar eine weit abgelegene Zahl auf den Namen eines geliebten Menschen tauft und diesen Namen in ein bedeutungsloses Register einträgt.
Natürlich würde unsere Firma viel länger im Geschäft bleiben als die Unternehmer, denen allmählich die Sterne ausgehen. In Wirklichkeit hätten wir nämlich überhaupt keinen Fortschritt bei der Benennung aller Zahlen gemacht, ganz gleich, wie viele Zahlen wir für unsere Klientel der Zahlenliebhaber benennen werden – unendlich viele bleiben noch ohne Namen. Angesichts dieser Gedanken haben Sie womöglich schon ein Auge auf die 500-stellige Zahl geworfen, die wir in diesem Sportwetten-Portal berühmt gemacht haben, und möchten ihr zu Ehren einer lieben Verwandten einen Namen geben. Vielleicht können wir sie die Tante-Hildchen-Zahl nennen. (Bitte überweisen Sie uns das Geld.)
Einer Zahl ein Gesicht zuordnen
Eine 500-stellige Zahl hat für uns keinerlei Bedeutung. Aber unsere moderne Welt zwingt uns, insbesondere durch die Allgegenwart von Computern, uns mit Zahlen im Millionen-, Milliarden- und sogar im Billionenbereich auseinanderzusetzen. Versteht man die Unterschiede zwischen diesen enormen Mengen, dann hat das manchmal ganz reale Konsequenzen. Um ein Gefühl für die Unterschiede zwischen Millionen, Milliarden und Billionen zu bekommen, sollten wir uns ein paar Szenarios anschauen, in denen sie zutage treten.
Tausende. Ein erhabenes Beispiel für eintausend ist annähernd die Zahl der Sterne, die man mit bloßem Auge am Nachthimmel sehen kann. Tatsächlich haben Tycho Brahe und Johannes Kepler im 17. Jahrhundert 1005 Sterne gezählt (wenngleich sie nie daran gedacht haben, sie zu verkaufen). Natürlich können Sie zu einem leicht unterschiedlichen Ergebnis kommen. Die Anzahl der Stunden, die ein Student während seiner College-Ausbildung im Unterricht verbringt, schwankt zwischen ein- und zweittausend, was ungefähr der Stundenzahl entspricht, die wir im Laufe eines Jahres schlafen. Ein Zufall? Wir glauben nicht…
Millionen. Um uns mit noch unhandlicheren Mengen vertraut zu machen, lassen wir uns auf ein paar Gedankenexperimente ein. Um der Größenordnung der Million einen Sinn abzugewinnen, denken wir an ei n paar Ansammlungen, die in Millionen gemessen werden. Ein hochauflösendes digitales Bild hat einige Megapixel. Mega bedeutet ungefähr eine Million; vielleicht nennen wir Prominente aus dem Showbusiness deshalb Megastars, weil sie viele Millionen wert sind.
Doch wir wollen schon ein etwas konkreteres Bild einer Million bekommen und denken daher über die gewichtige Frage nach: Wie viel würde eine Million Dollar wiegen? Nehmen wir an, eine verschmitzte Person böte uns eine Million Dollar in Eindollarscheinen an, allerdings unter der Bedingung, dass wir sie allein und auf einmal forttragen müssten. Ist das leichtes Geld? Wie viel genau wiegt eigentlich eine Million Dollar?
Wenn wir natürlich ein Bündel mit tausend Eindollarnoten herumliegen hätten, könnten wir sie einfach abwiegen und mit tausend multiplizieren. Da die meisten von uns aber nicht unbedingt so viele Einer besitzen, wollen wir eine etwas vertrautere Papiermenge ins Auge fassen. Eine Packung Druckerpapier wiegt ungefähr 4 Pfund und enthält genau 500 Blatt. Jeder Geldfälscher könnte uns auf Anhieb sagen, dass auf ein Blatt Kopierpapier ungefähr fünf Eindollarscheine passen. Also müssten etwa 5 X 500 oder 2500 Eindollarnoten ungefähr so viel wiegen wie eine Packung Kopierpapier. Eine Million sind 2500 X 400. Demnach können wir schätzungsweise sagen, dass eine Million Eindollarscheine ungefähr 4 X 400 beziehungsweise 1600 Pfund wiegen würden! Selbst Gouverneur Arnold Schwarzenegger hätte Schwierigkeiten, eine Million Dollar in Einerscheinen wegzutragen – eine unglückliche Erkenntnis, denn der großartige Staat Kalifornien könnte das Bargeld sehr gut gebrauchen.
Milliarden. Die bedeutendste Menge, die in Milliarden gemessen wird, sind wir selbst – das heißt, die gesamte Menschheit. Wir zählen rund 6,4 Milliarden. Und das Alter des Universums seit dem Urknall ist, wie oben schon erwähnt, 13,7 Milliarden Jahre. Ein Gigabyte bedeutet rund eine Milliarde Bytes. Unsere Festplatten bieten daher ein weiteres Beispiel für Milliarden.
Aber diese Beispiele für Milliarden tragen kaum dazu bei, dass unsere Vorstellungskraft solche beeindruckend riesigen Mengen erfasst. Um uns tatsächlich Milliarden vorstellen zu können, sollten wir einmal an Bill Gates denken. Vor ein paar Jahren konnte Bill Gates sich über ein Geschäftsjahr freuen, in dem sein persönliches Vermögen um zwanzig Milliarden Dollar anstieg. Wir können dieses atemberaubende Einkommen ins rechte Licht rücken, indem wir uns folgendes Szenario vorstellen.
Eines schönen Tages im Verlauf des Jahres, in dem Mr. Gates zwanzig Milliarden Dollar verdient, schuftet er in seinem winzig kleinen Arbeitszimmer und sieht einen Hundertdollarschein auf dem Fußboden liegen. Wäre er besser dran, wenn er die Arbeit für den Augenblick unterbrechen würde, den es dauerte, um den Geldschein aufzuheben, oder sollte er ihn ignorieren und weiter sein Gehalt verdienen?
Da es Mr. Gates eine oder zwei Sekunden kosten würde, herunterzulangen und den Hundertdollarschein aufzuheben, müssen wir sein Gehalt pro Sekunde berechnen. Nehmen wir an, er arbeitet 40 Stunden pro Woche und 50 Wochen im Jahr, dann arbeitet er im Lauf des Jahres 2000 Stunden. Jede Stunde hat 3600 Sekunden, also arbeitet er 2000 X 3600 beziehungsweise 7 200000 Sekunden pro Jahr. Da er 20000000000 Dollar verdient, beträgt sein sekündliches Gehalt 20000000000/720000- das sind ungefähr 2800 Dollar pro Sekunde.
Demnach verdient er jede achtundzwanzigstel Sekunde 100 Dollar. Weltklassesprinter mit außerordentlich schnellen Reflexen benötigen eine zehntel Sekunde, um auf den Startschuss zu reagieren, was mehr als doppelt so lange ist, wie Mr. Gates braucht, um 100 Dollar zu verdienen. Also sollte Mr. Gates sich nicht bücken, um den Einhundertdollarschein aufzuheben. Er sollte nicht einmal hinschauen. Milliarden sind eine Riesenmenge.
Sardinen. Ständig sprechen wir davon, die Welt sei überbevölkert. Aber womöglich sind die Orte, an denen die Menschen leben, das eigentliche Problem. Angenommen, wir laden die ganze Menschheit zu einer jährlichen Zusammenkunft in der Innenstadt ein. Würden sie alle ins Konferenzzentrum passen? Würden sie überhaupt in die Stadt passen?
Überraschung. Die gesamte Bevölkerung des Planeten könnte in ein hohes Stadthaus passen. Nein, natürlich nicht. Das war nur ein Jux. Aber tatsächlich könnten alle 6,4 Milliarden Menschen in einer Kubikmeile leben.
Rechnen wir’s aus. Eine Meile sind 5280 Fuß. Also sind eine Kubikmeile 150 Milliarden Kubikfuß (5280 Fuß X 5280 Fuß X 5280 Fuß). Wie viel Platz würde jeder der 6,4 Milliarden Erdbewohner darin haben? Nun ja, 150 Milliarden Kubikfuß geteilt durch 6,4 Milliarden Menschen sind ungefähr 23 Kubikfuß (etwa 7 Kubikmeter) pro Person – eine Menge Platz. Dieses Einkubikmeilenmotel hätte vielleicht nicht gerade die Annehmlichkeiten eines Fünfsternehotels, aber wir könnten uns tatsächlich alle hineinquetschen.
Billionen. Billionen kommen im Alltag nicht so häufig vor. Allerding gibt es ein bestürzendes Beispiel für Billionen, nämlich das Haushaltsdefizit der USA, das sich im Januar 2004 auf genau 7 Billionen Dollar belief, das sind 7000000000000 Dollar. Und das ist nun wirklich eine Riesenzahl. Wie ließe sich unsere Vorstellungskraft ankurbeln, um eine solche erstaunliche Zahl zu begreifen? Lassen Sie uns über eine Abzahlung spekulieren.
Angenommen, wir meinten es ernst mit der Schuldenverringerung und ein finanzwissenschaftlich versierter Gesetzgeber setzte sich energisch für ein Gesetz ein, das die Schulden um eine Million Dollar pro Stunde reduzierte. Da hieße es wirklich, den Gürtel enger zu schnallen, aber zumindest könnten wir greifbar sehen, wie sich die Schulden verringerten. Wie lange würden wir bei dieser hohen Geschwindigkeit brauchen, um die Schulden abzubezahlen? Nun, es würde uns offensichtlich 7 Billionen Dollar (7000000000000) geteilt durch 1 Million (1000000) Stunden kosten – das sind 7 Millionen (7000000) Stunden. Bei 365 Tagen pro Jahr und 24 Stunden pro Tag ergibt das 365 X 24 = 8760 Stunden pro Jahr. Teilen wir nun die zur Rückzahlung der Schulden erforderlichen 7000000 Stunden durch die 8760 Stunden eines jeden Jahres, dann sehen wir, dass bei einer Schuldenreduzierung von einer Million Dollar pro Stunde wir etwa 800 Jahre brauchen würden, um diese Schulden abzubezahlen.
Billiarden. Unser erster Schritt auf eine Billiarde zu (1000000000000000) besteht darin, ein Stück Papier einmal in der Mitte zu falten. Dann falten wir es noch einmal mittig und noch einmal und wiederholen diesen Schritt immer wieder (Abbildung 5.1). Könnten wir dieses Stück Papier nur 50-mal falten – was in der Praxis absolut unmöglich ist -, dann ließe sich mit diesem theoretischen Experiment ein Stapel Papier hervorbringen, der so unglaublich hoch ist, dass die Anzahl seiner Schichten, nämlich eine Billiarde, die Staatsschulden mickrig aussehen lässt. Wir wollen uns nun ansehen, warum das so ist.
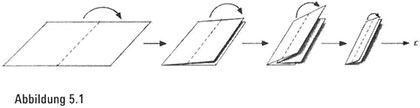
Wenn wir das Papier zum ersten Mal falten, ist das gefaltete Blatt
zwei Schichten stark. Wenn wir es ein zweites Mal falten, ist das gefaltete Papier vier Schichten stark. Nach jeder neuen Faltung hat das gefaltete Papier doppelt so dicke Schichten wie zuvor. Nach den ersten paar Faltungen wird die Anzahl der Schichten allmählich wirklich groß:
3 Faltungen – 8 Schichten
4 Faltungen – 16 Schichten
5 Faltungen – 32 Schichten
6 Faltungen – 64 Schichten
7 Faltungen – 128 Schichten
8 Faltungen – 256 Schichten
9 Faltungen – 512 Schichten
Nach 10 Faltungen hätten wir 1024 Schichten. Könnten wir also ein Blatt Papier zehnmal falten – was uns nie gelingen wird wäre das gefaltete Papier 1024 Schichten stark, was etwa zwei Paketen Kopierpapier entspricht – beziehungsweise rund 12 Zentimetern Höhe.
Während wir also weiter falten und mit jeder Faltung die Stärke und Anzahl der Schichten verdoppeln, stellen wir fest, dass der Turm ziemlich schnell an Höhe gewinnt (Abbildung 5.2). Nach 20 Faltungen haben wir mehr als eine Million Schichten mit einer Gesamtstärke, die die Länge eines Fußballplatzes überschreitet. Nach 30 Faltungen haben wir eine Milliarde Schichten, die insgesamt 102,4 Kilometer stark sind. Nach 40 Faltungen erreichen wir eine Billion Papierschichten. Nach 42 Faltungen sind wir schon am Mond vorbei. Nach 50 Faltungen haben wir eine Billiarde Schichten erreicht, und wenn wir jetzt das Papier nur noch ein einziges Mal falten, ist es 204,8 Millionen Kilometer stark, was weiter ist als die Entfernung zwischen Erde und Sonne! Wiederholtes Verdoppeln ist ein explosiver Prozess.
| Faltungen | Schichten (ungefähre Anzahl) | Stärke (ungefähre) |
| 10 | 1000 (eintausend) | 12 Zentimeter |
| 15 | 3,35 Meter | |
| 20 | 1 000000 (eine Million) | 1066 Meter |
| 25 | 3,2 Kilometer | |
| 30 | 1 000000000 (eine Milliarde) | 102,4 Kilometer |
| 35 | 3200 Kilometer | |
| 40 | 1 000000000000 (eine Billion) | 102 400 Kilometer |
| 45 | 3200000 Kilometer | |
| 50 | 1 000000000000000 (eine Billiarde) | 102400000 Kilometer |
| 51 | 204800 000 Kilometer |
Abbildung 5.2
Mit dem Beispiel des Papierfaltens sind wir zu einer Erkenntnis gekommen, die unserer Intuition zuwiderläuft: dass wir nämlich mit erstaunlich wenigen Schritten riesige Zahlen erzeugen können. Als Nächstes werden wir eine Realität in entgegengesetzter Richtung kennen lernen, auf die wir intuitiv nicht kommen würden. Wir werden nämlich feststellen, dass zwei beliebig große Mengen durch überraschend wenige Schritte miteinander verbunden sind.
Das Taxieren von Zahlen und ihre Bedeutung bei den Glücksspielen Teil 2


