Von präziser Schönheit zu reinem Chaos – Glücksspiele Tipps Teil 2

Von präziser Schönheit zu reinem Chaos – Glücksspiele Tipps Teil 1

Woher kommt die Anziehungskraft?
Warum gibt es auf den Goldenen Schnitt abgestimmte Proportionen in so vielen Kunstwerken? Ausgerüstet mit der Erfahrung unserer geometrischen Konstruktionen, kehren wir zu der von

Le Corbusier entworfenen Villa zurück. Hier hat er unverhohlen das Goldene Rechteck integriert, das wir inzwischen unter neuen, fundierten Gesichtspunkten sehen. Vor allem hat ja unser Konstruktionsverfahren eine natürliche Verbindung zwischen einem Goldenen Rechteck und dem in ihm enthaltenen größten Quadrat hervorgebracht. Wenn wir uns nun Le Corbusiers Villa anschauen, müssen wir einfach feststellen, dass hier auf ganz ähnliche Weise der Wohnraum auf der rechten Seite ein großes Quadrat darstellt (Abbildung 7.15).

Also finden wir in Le Corbusiers Entwurf tatsächlich die gleiche geometrische Konstruktion des Goldenen Rechtecks, die wir gerade skizziert haben. Wir fangen mit dem quadratischen Wohnraumteil der Villa an und fügen dann die offene Veranda auf der linken Seite hinzu, um die rechtwinklige Anziehungskraft der Villa in ihrer Gesamtheit hervorzurufen. Gibt es irgendetwas Besonderes an dem rechtwinkligen Verandateil, das erforderlich wäre, um das Goldene Rechteck zu vollenden? Wenn wir uns darauf konzentrieren, es auf die Seite legen und vergrößern, erkennen wir eine unerwartete Übereinstimmung: Dieses Rechteck scheint ein weiteres Goldenes Rechteck zu sein (Abbildung 7.14). Eigentlich ist

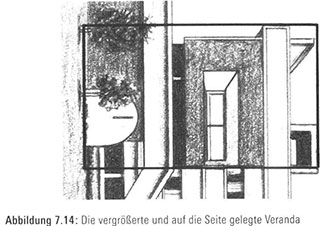
diese architektonische Beobachtung eine mathematische Tatsache. Ließen wir das größte, im Goldenen Rechteck enthaltene Quadrat weg, bliebe uns immer noch das kleine Nachwuchsrechteck als Goldenes Rechteck erhalten. Und was den Genuss noch steigert, ist die Tatsache, dass diese schöne mathematische Wahrheit aus der wunderbaren, fortlaufenden Bruchdarstellung folgt, die wir im vorausgegangenen Kapitel für

Die Goldenen Exemplare
Nun wollen wir uns davon überzeugen, dass uns tatsächlich ein weiteres Goldenes Rechteck erhalten bleibt, wenn wir das größtmögliche Quadrat aus einem Goldenen Rechteck entfernen. Gehen wir also von einem Goldenen Rechteck mit der Höhe i aus. Definitionsgemäß muss die Grundlinie /f/ sein, da das Verhältnis zwischen Grundlinie und Höhe /f/ sein muss. Wenn wir daher das größtmögliche Quadrat entfernen (Abbildung 7.15), können wir leicht die Ausmaße des kleineren verbleibenden Rechtecks bestimmen: 1 X (f – 1). Um zu überprüfen, dass dieses kleinere Rechteck tatsächlich ein Goldenes Rechteck ist, müssen wir beweisen, dass die Länge der längeren Seite dividiert durch die Länge der kürzeren Seite dem Goldenen Schnitt

Wir sind wieder bei folgendem wunderschönen Muster angelangt:

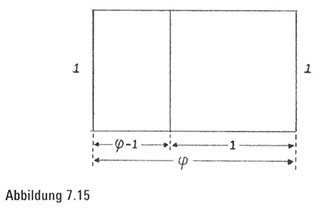
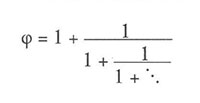
Wenn wir von jeder Seite dieser Gleichung i subtrahieren, sehen wir, dass

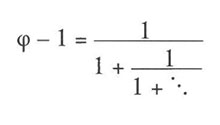
und wenn wir daher beide Seiten umkehren, um 1 / (f – 1) zu erhalten, entdecken wir, dass

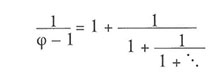
was genau /f/ ist! Wir sehen also, dass das Verhältnis zwischen Grundlinie und Höhe des kleineren Rechtecks der Goldene Schnitt ist und dass deshalb das Nachwuchsrechteck ein kleines Goldenes Rechteck ist.

Tatsächlich ist das Goldene Rechteck das einzige Rechteck, das die Eigenschaft besitzt, nach der Entfernung des größmöglichen Quadrats ein Nachwuchsrechteck zu hinterlassen, dass dieselben Proportionen von Länge zu Breite hat wie das ursprüngliche elterliche Rechteck. Hiermit haben wir eine wesentliche Eigenschaft aufgedeckt, die nur das Goldene Rechteck besitzt. Vielleicht erklärt diese einzigartige, rechtwinklige Ähnlichkeit, warum das Goldene Rechteck in ästhetischer Hinsicht so angenehm wirkt.

Ein endloser Stammbaum des Rechtecks
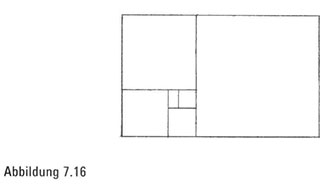
Zu den vielen Lektionen, die uns die Mathematik lehrt, gehören die neuen Einsichten, die sich einstellen, sobald wir eine neue Idee entdecken und diese auf die Spitze treiben. In unserem Fall haben wir entdeckt, dass beim Entfernen des größtmöglichen Quadrats aus einem Goldenen Rechteck das übrig bleibende Rechteck ebenfalls ein Goldenes ist. Und was nun? Wir können den Vorgang wiederholen! Nehmen wir also einfach von unserem goldenen Nachwuchsrechteck das größte Quadrat weg. Was bleibt übrig? Ein noch kleineres goldenes Enkelrechteck. Natürlich könnten wir den Prozess beliebig lange fortsetzen und dadurch eine Kollektion
ewig weiter schrumpfender Goldener Rechtecke erzeugen (Abbildung 7.16).

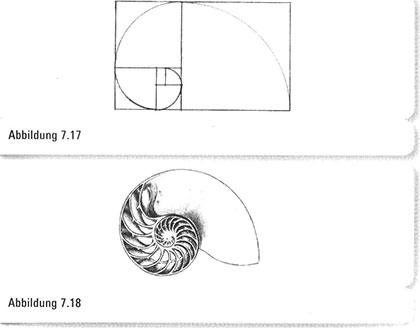
Wenn wir unsere Abbildung anschauen und in jedes Quadrat einen Viertelkreis setzen, entsteht eine wunderschöne Spirale (Abbildung 7.17). Diese Spirale ist eine gute Annäherung an eine logarithmische Spirale, die mathematische Abstraktion einer natürlichen Kurve, wie sie in der anmutigen Nautilusmuschel vorkommt (Abbildung 7.18).

Und wieder einmal erkennen wir, wie mathematische Entdeckungen unser Verständnis von der Natur geprägt und unseren Sinn für künstlerische Schönheit erweitert haben.

Narrengold
Obwohl wir viele Abbildungen gesehen haben, in denen das Goldene Rechteck sowohl unbeabsichtigt als auch auf natürliche Art und Weise in Kunst und Natur unabsichtlich auftrat, ist es andererseits ebenso wahr, dass nicht alle Rechtecke Goldene Rechtecke sind, wie sehr wir auch unsere Vorstellungskraft bemühen. Trotz dieser Erkenntnis haben manche Leute versucht, sie auch dort zu sehen, wo sie nicht sind.

Kehren wir in die Welt der Kunst zurück und schauen uns eine Tintenzeichnung von Le Corbusier an, die aus dem Jahr 1946 stammt und Der Modulor heißt (Abbildung 7.19). Hier sehen wir seinen Versuch, den menschlichen Körper in fibonacciähnliche Muster zu dekonstruieren. Die Zahlen, die er am unteren Ende der Zeichnung auflistet, stellen die Größenmessungen verschiedener Körperteile dar. Am unteren Ende der Liste sehen wir 6 und dann 9. Addieren wir beide Zahlen, erhalten wir die nächste Zahl auf der Liste und so weiter. Folglich erkennen wir ein Fibonacci-Muster – aufgrund unserer Entdeckungen aus dem letzten Kapitel sehen wir darin eigentlich das Beispiel einer Wiederholungssequenz mit den Anfangssamenkörnern 6 und 9. Wie wir dort lernten, nähert sich das Verhältnis der aufeinanderfolgenden Terme dem Goldenen Schnitt.

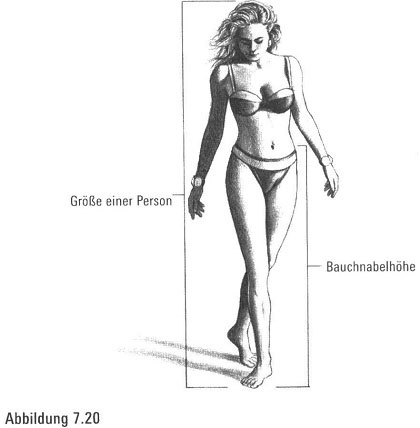
Der Bauchnabel in Le Corbusiers Zeichnung erinnert uns an einen amüsanten Mythos. Manche Leute glauben, dass bei de idealen menschlichen Körperform die Größe einer Person, geteilt durch die Länge des Abstands vom Bauchnabel bis zu den Füßen, den Goldenen Schnitt erzeuge (.Abbildung 7.20). In der Privatsphäre Ihrer Wohnung sollten Sie sich ungezwungen genug fühlen, diese Messungen vorzunehmen, um herauszufinden, wie nahe Sie dem Ideal kommen.

Vorsichtshalber weisen wir darauf hin, dass diese Theorie nie wissenschaftlich oder mathematisch bewiesen wurde. Also verzweifeln Sie bitte nicht, wenn Sie den Idealwert nicht erreichen. Manch einer glaubt, die rechteckigen Ausmaße des Handtellers stimmten mit dem Goldenen Rechteck überein. Also seien Sie bitte so frei und messen Sie Ihre Hand nach, um zu sehen, ob sie dem platonischen Mythos ästhetischer Wirkung entspricht. Fällt uns das Goldene Rechteck in unserer Umgebung auf oder nicht? Ist es im Parthenon zu sehen? Ist die Position unseres Bauchnabels dafür ein Kriterium? Vielleicht halten wir ja das Goldene Rechteck buchstäblich in unseren Händen. Vielleicht aber auch nicht.

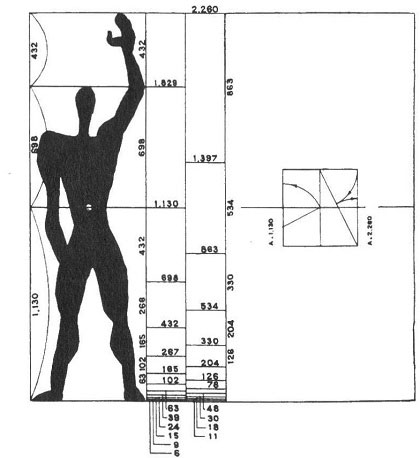
Abbildung 7.19: In Der Modulor (1946) sehen wir, wie Le Corbusier fibonacciähnliche Muster erzeugt: 6 + 9 = 15, 9 + 15 = 24 und so weiter.

Ein Goldenes Dreieck
Die Schlüsselfigur bei der Bestätigung, dass wir mit unserer geometrischen Konstruktion tatsächlich ein Goldenes Rechteck erzeugen, war kein Rechteck, sondern vielmehr ein Dreieck. Eigentlich war es rechtwinkliges Dreieck, dessen einer Schenkel doppelt so lang war wie der andere. Hier nennen wir eine solche Figur ein Goldenes Dreieck, weil es von so entscheidender Bedeutung für die geometrische Konstruktion des Goldenen Rechtecks ist

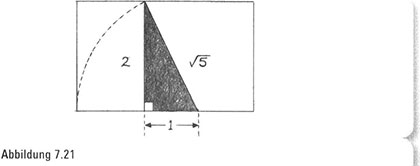
(Abbildung 7.21). Außerdem hat das Goldene Dreieck ganz eigene einzigartige Merkmale, die eine Herausforderung für unseren ästhetischen Geschmack sind. Deshalb wollen wir dieses Kapitel mit einer kurzen Erforschung der Geschichte des Goldenen Dreiecks beschließen und sehen, wie dies zu einem bemerkenswert betörenden Bild des geordneten Chaos führt.

Bis zu diesem Punkt des Kapitels feierten wir die rechteckige Form und ignorierten die Nuancen und die dreiwinklige Schönheit des Dreiecks. Ein ganz gewöhnliches Dreieck ohne besondere Seitenlangen und ohne besondere Winkel mag zunächst wenig aufregend erscheinen, aber es hat auf jeden Fall eine interessante Eigenschaft: Wenn wir vier Kopien davon anfertigen, können wir diese Dreiecke unmittelbar so zusammensetzen, dass wir ein Dreieck erhalten, das die gleichen Proportionen hat wie das ursprüngliche Dreieck, nur in einem größeren Maßstab. Dieses größere ähnliche Dreieck ist tatsächlich doppelt so groß wie das Original – das heißt, jede Seite ist doppelt so lang wie die entsprechende Seite des ursprünglichen Dreiecks (.Abbildung 7.22).

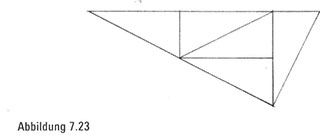
Allerdings besitzt das Goldene Dreieck ein einzigartiges Merkmal, das alle anderen Dreiecke nicht vorweisen können – eine Eigenschaft, die, wie manche Leute glauben, es zum ästhetisch reizvollsten Dreieck macht. Das Goldene Dreieck ist nämlich das einzige rechtwinklige Dreieck, das aus fünf Kopien zusammengesetzt werden kann, um eine größere Kopie seiner selbst zu erzeugen (Abbildung 7.23). Wie das geht? Der kurze Schenkel unseres großen Dreiecks ist genau die Hypotenuse des ursprünglichen rechtwinkligen Dreiecks, während der größere Schenkel aus zwei Hypotenusen besteht. Folglich erkennen wir, dass der eine Schenkel unseres großen rechtwinkligen Dreiecks doppelt so lang ist wie der andere und daher selbst ein Goldenes Dreieck ist. Wir können nun diesen faszinierenden Neubildungsprozess anwenden, indem wir fünf Kopien jedes beliebigen Goldenen Dreiecks nehmen und sie zusammensetzen, um ein noch größeres Goldenes Dreieck zu erhalten.

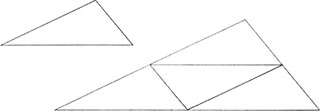
Abbildung 7.22: Gegeben sei ein beliebiges Dreieck, von dem vier Kopien zu einem ähnlich proportionierten Dreieck zusammengesetzt werden können, dessen drei Seiten jeweils doppelt so lang sind.

Sollten wir an dieser Stelle damit aufhören? Natürlich nicht.

Mathematische Muster sind wie Kartoffelchips – wir können nicht einfach schon nach ein paar Handvoll aufhören. Wir wissen alle, wohin das wiederholte Einwerfen von Kartoffelchips führt – zu einem ansehnlichen Rettungsring um die Taille. Auf ganz ähnliche Weise führt die Wiederholung dieses Neubildungsprozesses des Goldenen Dreiecks zu einer ständig zunehmenden Menge Goldener Dreiecke, die alle dringend etwas Bewegung nötig hätten. Was aber geschähe, wenn wir sagten: Zur Hölle mit den Weight Watchers!, und ließen diese Goldenen Dreiecke ewig weiterwachsen ?

Sich fortpflanzendes Chaos
Wenn wir nun den ganz gewöhnlichen Neubildungsprozess mit nur vier Exemplaren eines beliebigen Dreiecks wiederholen, wird die gesamte Fläche zu einem mosaikartigen Muster, das heißt, wir erzeugen eine endlose Parkettierung (.Abbildung 7.24). Auf diese Weise haben wir unendlich viele Kopien einer willkürlich proportionierten dreieckigen Kachel, die wir Zusammenlegen können, um größere, aber ähnliche Versionen der ursprünglichen Kachel zusammenfügen können. Setzen wir den Prozess bis ins Unendliche fort, wird die gesamte Fläche mit Kacheln einer einzigen Größe parkettiert.

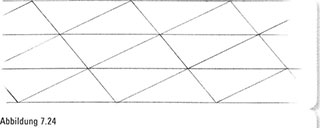
Wenn wir das von dieser Parkettierung erzeugte Muster betrachten, erkennen wir eine beruhigende Wiederholung in dem Muster, das wohltuend und anziehend zugleich ist. Unbewusst registrieren wir dabei erstaunlich viel Symmetrie in dieser Parkettierung. Wenn wir das Mosaik um ein Dreieck verschieben würden, stimmte das neue Parkett genau mit seiner ursprünglichen Version überein. Wir können unser Parkett in viele Richtungen verschieben und werden stets zu dem Ergebnis kommen, dass die Neupositionierung perfekt mit dem ursprünglichen Mosaik übereinstimmt. Wir sagen daher, diese Parkettierung habe eine Verschiebungssymmetrie- das heißt, wir können das gesamte Bild in gewisse Richtungen übersetzen oder verschieben, ohne dass sich etwas verändert.

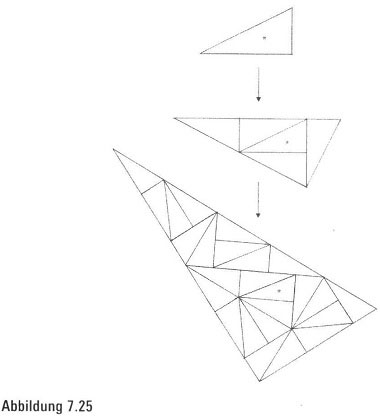
Wenn wir jetzt ein hohes Darlehen aufnähmen und unendlich viele Kacheln eines Goldenen Dreiecks kauften, könnten wir die gesamte Fläche durch wiederholtes Aneinanderreihen Supergoldener Dreiecke parkettieren. Das heißt, wir fangen damit an, fünf Kacheln zusammenzulegen, die unsere Superkachel sein soll. Anschließend legen wir fünf Exemplare dieser Superkachel zu einer Megasuperkachel zusammen, die auch ein Goldenes Dreieck ist (Abbildung 7.25). Diesen Prozess können wir wiederholen. Wenn wir das tun, sieht die zustande kommende Parkettierung überraschenderweise ziemlich chaotisch und durcheinandergeraten aus (Abbildung 7.26).

Wir können in der Tat beweisen, dass es keine Verschiebung dieser Parkettierung gibt, die zu einer perfekten Übereinstimmung jener verschobenen Version mit der Ausgangslage führt. Dieses Mosaik, auch als Windradparkettierung bekannt, ist aperiodisch, was heißt, dass es kein wiederholtes Muster enthält, das uns gestattete, das ursprüngliche Muster nach einer Verschiebung wiederherzustellen.

Den Ausschlag für die Bezeichnung Winradpakettierung gab die Tatsache, dass die zunehmend größer werdenden Superkacheln, die während der Konstruktionen entstehen, umherwirbeln und in wirklich jede mögliche Richtung zeigen. Von diesem chaotischen Bild geht allerdings auch eine Anziehungskraft aus, die gerade auf dem Unstimmigen beruht. Das Windradmuster kommt zwar einem ziemlich dramatischen Abschied von der klassischen Schönheit des Goldenen Rechtecks gleich, aber es ist auch eine moderne Form mathematischer Kunst, die möglicherweise unseren künftigen ästhetischen Geschmack bestimmen wird.

Unsere Goldene Reise
Unsere Reise ins Reich der Ästhetik und ins Altertum mit seinen Goldenen Rechtecken führt uns zu einer spektakulären Erkenntnis, die nicht nur mit Spiralen, Kunst und Musik zu tun hat, sondern auch mit unserem persönlichen Potenzial, die Welt klarer zu sehen. Wie oft haben wir nicht schon Eigenschaften der Natur gesehen, ohne uns um die Details und um die vielfältige Struktur zu kümmern, die eine vereinigende Kraft darstellt. Mit Hilfe einfacher Gedankenexperimente – in diesem Kapitel durch die Suche nach den grundlegenden Neubildungseigenschaften des Goldenen Rechtecks verdeutlicht – lernen wir, die Welt anders zu betrachten. Wir erkennen plötzlich Muster.

Wo verstecken sich all die Strukturen, die nur darauf warten, von uns entdeckt zu werden? Sobald wir ein Objekt im hellen Licht konzentrierter Einfachheit etwas sorgfältiger betrachten, entfaltet sich eine ganze Geschichte. Eingestimmt aufs Detail, wird uns plötzlich eine Welt der Schönheit bewusst, die von mathematischen Mustern durchdrungen ist. Jetzt erkennen wir, dass Ästhetik und Mathematik eng miteinander verbunden sind. Es gibt Schönheit in der Mathematik und Mathematik in der Schönheit.