Von präziser Schönheit zu reinem Chaos – Glücksspiele Tipps Teil 1

Ästhetische Darstellung durch die Linse der Mathematik
Die mathematischen Wissenschaften stellen insbesondere Ordnung, Symmetrie und Einschänkungen dar; und dieses sind die großartigsten Formen der Schönheit.
Aristoteles

Offensichtlich … Der Parthenontempel in Griechenland, Debussys Komposition Vorspiel zu Der Nachmittag eines Fauns und die Position Ihres Bauchnabels haben absolut nichts miteinander zu tun.

Überraschung … Die Anziehungskraft, die der Goldene Schnitt ausübt, vereint Parthenon und Debussy, und womöglich kann er auch die perfekte Stelle für unsere Bauchnabel lokalisieren. Wenn wir uns das platonische Ideal von Schönheit und Form zu eigen machen, werden wir mit der realen Möglichkeit konfrontiert, dass die Mathematik unseren ästhetischen Geschmack prägt und bestimmt, was wir als attraktiv wahrnehmen.

Proportionen mit Schwung – das attraktivste Rechteck
Machen Sie romantische Musik an, machen Sie es sich auf einem Zweiersofa gemütlich, schließen Sie die Augen und stellen Sie sich das ideale Rechteck vor – weder allzu quadratisch noch allzu gestreckt. Lassen Sie diese Vorstellung in Ihrem Kopf tanzen und Ihre Fantasie anregen, während Sie die vier Rechtecke in Abbildung 7.1 betrachten, und legen Sie sich auf das Exemplar fest, das dem Ihnen vorschwebenden Rechteck am nächsten kommt.

Überraschung. Haben Sie das dritte Viereck von links gewählt? Viele Leute träumen von ihm. Wir müssen allerdings zugeben, dass es bei uns keinen Erdrutschsieg davontragen würde, wenn wir eine Wahl durchführen müssten. Bei der Wahl zum Sieger des Rechteckpreises könnte es in der Tat zu einer Neuauflage des Albtraums kommen, der im Jahr 2000 bei der US-Präsidentschaftswahl in Florida stattfand (als die hängen gebliebenen Stanzreste in Wahlscheinen womöglich ausschlaggebend für den Wahlausgang gewesen sind). Eine satte Mehrheit jedoch würde sich zu diesem dritten Rechteck hingezogen fühlen, was dem Obersten Gerichtshof ein Grundsatzurteil im Prozess Grundlinie vs. Höhe ersparen würde.

Rechtecke kommen, genau wie Menschen, in vielerlei Gestalt vor – schlank und dünn, klein und untersetzt und in allen möglichen Zwischenstufen. Manche Vierecke aber sind so elegant proportioniert, dass wir sie Goldene Rechtecke nennen. Ihre Proportionen sind atemberaubend anzusehen. Ein solches Rechteck stellt die Quintessenz, das sine qua non der Rechtwinkligkeit dar – kurzum, es ist das attraktivste Rechteck aller Klassen. Die Proportionen, die diesen Überschwang erzeugen, sind eng mit dem Goldenen Schnitt verbunden – der Zahl, die auf natürliche Weise aus Tannenzapfen, Ananas und Gänseblümchen hervorging.

Später in diesem Sportwetten-Portal entdeckten wir, dass die in der Natur vorkommenden Spiralen den Kabinengästen auf der Arche Noah nicht unähnlich sind: Sie kommen paarweise vor – eine Zahl steht für die Spiralen in einer Richtung, während die andere Zahl die Spiralen in der entgegengesetzten Richtung angibt. Gemeinsam bilden diese Abzählungen der Spiralenpaare die aufeinanderfolgenden Terme in der Liste der Fibonacci-Zahlen: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 und so weiter. Die Verhältnisse fortlaufender Terme in dieser idealisierten Sequenz abgezählter Spiralen nähern sich dem außerordentlich attraktiven Goldenen Schnitt, der mit dem griechischen Buchstraben Phi bezeichnet wird und dem numerischen Wert von 1,618 … entspricht.

Ein Goldenes Rechteck ist ein Rechteck, für das das Verhältnis zwischen Grundlinie und Höhe der Goldene Schnitt ist. Das dritte Rechteck in Abbildung 7.1 ist ein Beispiel für ein Goldenes Rechteck. Vierecke mit diesen Proportionen locken und verführen uns bei jeder Gelegenheit. Spüren Sie nicht auch den unerklärlichen Drang, Karteikarten zu benutzen? Sie liegen doch überall herum. Nehmen Sie eine in die Hand und überprüfen Sie ihre Abmessungen: 3X5 Zoll (10 X 15 Zentimeter) ist die Standardgröße, 5X8 Zoll (15 X 21 Zentimeter) ist die schöne große Version.

Das Verhältnis von Grundlinie zu Höhe dieser verführerischen Karteikarten sind 5/3 = 1,666 … und 8/5 = 1,600…, zwei Werte, die den mittlerweile vertrauten Ziffern 1,618 nahekommen, aus denen die digitale DNS des Goldenen Schnitts zusammengesetzt ist. Vielleicht kommt diese Tatsache für uns aber auch nicht allzu überraschend, denn beide Paare (sowohl 3 und 5 als auch 5 und 8) sind Paare fortlaufender Fibonacci-Zahlen. Vielleicht haben die freundlichen Leute in den Werbeagenturen auf der Madison Avenue in New York sorgfältig diese Dimensionen ausgesucht, um uns eine subliminale Botschaft zu übermitteln, die uns dazu verleitet, Karteikarten zu kaufen. Wir jedenfalls benutzen sie ständig.

Während eine Verbindung zwischen Mathematik und Madison Avenue über die Proportionen einer Karteikarte genauso dürftig und dünn zu sein scheint wie die Karteikarte selbst, gibt es viele wirkliche Beispiele, in denen wir den Widerspiegelungen des Goldenen Rechtecks in künstlerischen Werken aller Epochen der Menschheitsgeschichte begegnen. Mit den alten Griechen wollen wir anfangen.

Golden Oldies
Der Parthenontempel ist ein überragendes Beispiel klassischer Schönheit, dennoch wären wir wohl kaum begeistert, wenn unser Online-Reisebüro ihn als unsere Herberge während unseres Aufenthalts in Athen ausweisen würde. Machen wir uns nichts vor: Das Ding ist eine Ruine (.Abbildung 7.2). Aber das war nicht immer der Fall. Einst war der Parthenon der angesagte Ort schlechthin.

Damals hatte er sogar ein Dach. Aus den noch vorhandenen Dachfragmenten können wir uns eine Vorstellung machen, wie der Parthenon in seinen besten Tagen ausgesehen haben mag. Anschließend können wir ein Goldenes Rechteck darüberlegen, das nahezu perfekt das ganze alte Gebäude nebst neu gedecktem Dach umfasst (.Abbildung 7.5). Ist die Verbindung zwischen Parthenon und Goldenem Rechteck mit Absicht hergestellt worden, oder ist sie ein bloßer Zufall?

Bevor wir die Frage nach Design oder Zufall stellen, wollen wir uns ein weiteres Beispiel aus der antiken griechischen Kultur ansehen. Lange bevor es Einwegkontaktlinsen gab, benutzten die alten Griechen Objekte, die als Augenschalen bekannt waren, um ihre antiken griechischen Augen mit Augentropfen zu benetzen. Diese verzierten Schalen waren häufig mit einem Augenpaar geschmückt, das dem Blick des Betrachters begegnete und keinen Zweifel an
seinem Verwendungszweck ließ. Während wir also noch die an-mutigen Augenschalen-Kunstwerke bewundern, starren uns die Goldenen Proportionen geradewegs ins Gesicht (Abbildung 7.4). Setzen wir die Entfernung vom Ende des einen Henkels bis zum Schalenrand mit ½ fest, dann käme die Höhe der Schale dem Goldenen Schnitt überraschend nahe. Darüber hinaus gleicht die Länge der Schalenrundung 1 + f.

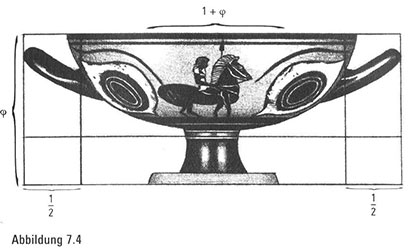
Wurden Goldener Schnitt und Goldenes Rechteck in diesen antiken Kunstwerken bewusst angewendet? Diese Frage bleibt bis heute unbeantwortet. Eine romantische Mutmaßung lautet, die Griechen hätten diese Proportionen auf der Grundlage eines natürlichen Sinns für Anmut und Schönheit unbewusst gewählt und auf diese Weise den inneren ästhetischen Reiz mit abstrakten mathematischen Konstruktionen vereint.

Göttliche Proportionen
Im Schnellvorlauf lassen wir eineinhalb Jahrtausende hinter uns und landen in der Renaissance. Leonardo da Vinci kannte das Goldene Rechteck und den Goldenen Schnitt. Er schuf sogar die Illustrationen für eine Abhandlung mit dem Titel De Divina Proportione. Der göttliche Goldene Schnitt taucht an vielen Stellen in seinem Werk auf. Sehen wir uns beispielsweise sein unvollendetes Porträt des heiligen Hieronymus an, dann erkennen wir, dass wir die Gestalt des Heiligen mit einem perfekten Goldenen Rechteck umrahmen können (Abbildung 7.5). Allerdings wissen wir nicht, ob Leonardo die Proportionen dieses sitzenden Heiligen absichtlich so gestaltet hat, damit sie dem Goldenen Rechteck entsprechen, oder ob rein ästhetische Vorlieben das Gleichgewicht der Figur diktierten.

Abbildung 7.5

Eine eigentlich grundsätzlichere und umstrittenere Frage lautet, ob die Proportionen des Goldenen Rechtecks überhaupt zu sehen sind. Wenn wir uns das darübergelegte Goldene Rechteck sorgfältig anschauen, können schon leise Zweifel aufkommen – der linke Rand dieses Rechtecks berührt weder die Figur noch den unteren Teil des Gewands. Dieser Rand schwebt aus dem einzig ersichtlichen Grund da draußen herum, um ein perfektes Goldenes Rechteck zu erzeugen.
Und tatsächlich scheint uns noch mehr vom goldenen Schimmer abhandenzukommen, wenn wir zum Parthenon zurückkehren und den unteren Rand des aufkopierten Rechtecks genauer untersuchen. Denn nun erkennen wir, dass das Goldene Rechteck zufällig auf der zweiten Stufe ruht. Ist also das Goldene Rechteck überhaupt vorhanden? Während für Mitglieder des Kults vom Goldenen Schnitt solche Beobachtungen Ketzerei sind, lässt sich in der Wirklichkeit kein perfektes Goldenes Rechteck bauen, da wir nicht in der Lage sind, die Dinge mit unendlicher Genauigkeit zu messen. Dennoch sind einige Einflüsse des Goldenen Rechtecks auf die Kunst unbestreitbar.

Wie ein Wirbelwind setzen wir unsere Reise durch die Kunstgeschichte fort und landen im Frankreich des Impressionismus. In diesem geschichtlichen Augenblick ließen sich die Künstler von wissenschaftlichen Vorstellungen inspirieren. Georges Seurat war ein Künstler, der dieses Zusammenspiel zwischen mathematischen Vorstellungen und Kunst begeistert aufgriff. Tatsächlich haben manche Beobachter behauptet, Seurat sei mit dem Bild des Goldenen Rechtecks im Kopf vor jede seiner Leinwände getreten. In Zirkusparade finden wir viele Goldene Rechtecke {Abbildung‘].6). Überdies konstruierte er die Verhältnisse unterschiedlicher Längen in seinen Werken, die dem Goldenen Schnitt schon sehr nahekommen. Sind da wirklich Goldene Rechtecke zu sehen? Was denken Sie?

Wenn wir jetzt zum Expressionismus und zum Modernismus wechseln, werden wir womöglich mit weißen Leinwänden oder, wenn wir Glück haben, mit Rechtecken konfrontiert. Piet Mondrian war ein Vertreter des Expressionismus und bekannt für sein Konzept der Zerstörung der Räumlichkeit, was auf die Fragmentarisierung des Raumes hinausläuft. Als Zeitvertreib, der dem Kinderspiel ähnelt, in sogenannten Wimmelbilderbüchern den Walter aus einer großen Anzahl ähnlich aussehender Gestalten herauszusuchen, können wir in Mondrians Bildern nach Goldenen Rechtecken suchen, die möglicherweise unter all den vielen Linien und Formen verborgen sind. Es heißt, Mondrian habe auf den Kommentar eines Betrachters, der alle Linien in seinem Werk kommentiert habe, geantwortet: Ich sehe überhaupt keine Linien. Ich sehe nur den Raum, der sie umgibt. Und natürlich müssen wir die möglichen Goldenen Rechtecke in genau diesen Räumen suchen.

Goldene Werke konstruieren und komponieren
Im Gegensatz zur öffentlichen Meinung glaubte der französischschweizerische Architekt Le Corbusier, der im 20. Jahrhundert lebte, mathematische Vorstellungen wirkten beruhigend auf das menschliche Leben. Zu den wohltuendsten Konzepten gehörte aus seiner Sicht das Goldene Rechteck, das er bewusst in viele seiner Arbeiten integrierte. In Abbildung 7.7 sehen wir seine französische Villa, die wir, sobald die Kamine mit einbezogen werden, mit einem nahezu perfekten Goldenen Rechteck umrahmen können. Tatsächlich fängt Le Corbusiers ästhetisch attraktives Milieu ein Merkmal ein, das nur unser bezauberndes Goldenes Rechteck besitzt.

Unsere Wertschätzung des Goldenen Schnitts muss nicht auf die visuelle Welt beschränkt bleiben. Tatsächlich können wir uns zurücklehnen und der Schönheit dieses verführerischen Formats lauschen. So war Claude Debussy vom Goldenen Schnitt fasziniert und strebte danach, diese Zahl in seinem musikalischen Werk einzufangen.

Insbesondere in seiner Komposition Vorspiel zu Der Nachmittag eines Fauns können wir durch konzentriertes Zuhören empfinden, wie sich uns der Goldene Schnitt durch Tonlage, Rhythmus und Dynamik mitteilt.

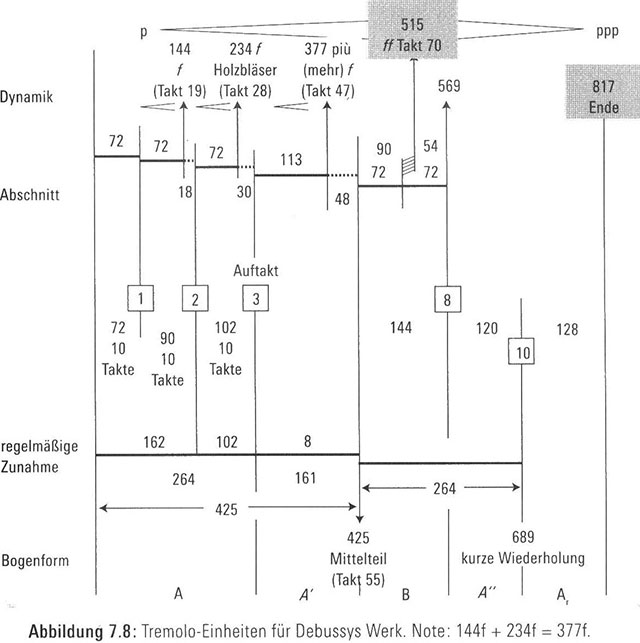
Musikalische Impulse werden auch Tremolo-Einheiten genannt. Messen wir die Tremolo-Einheiten von Vorspiel zu Der Nachmittag eines Fauns, erkennen wir ein paar interessante Muster. Debussy notierte bei den Takten 19 und 28 fortissimos (ff, sehr laut). Addieren wir diese beiden Werte, befinden wir uns bei Takt 47, beim nächsten fortissimo. Also erkennen wir die Widerspiegelungen des Fibonacci-Musters in Debussys musikalischem Werk (Abbildung 7.8). Tatsächlich offenbart die in der Graphik dargestellte Dynamik manch andere Fibonacci-Muster.

Die Komposition steigert sich zu einem dramatischen fortissimo bei Takt 70 und bewegt sich danach gemächlich auf ein pianissimo (ppp, äußert leise) zu. Das ganze Stück ist 129 Sekunden lang, während die Zeit zwischen dem Anfang des Stücks und jenem fantastischen fortissimo beim 70. Takt 81 Sekunden beträgt. Dividieren wir diese beiden Werte, erhalten wir 1,592 …, was auf eindrucksvolle Weise dem Goldenen Schnitt von 1,618 … nahekommt. Lässt sich ein Teil der Schönheit und Eleganz des Werks von Debussy auf die bewusste Verwendung des Goldenen Schnitts zurückführen? Obwohl wir diese Frage nicht mit Sicherheit beantworten können, können wir davon ausgehen, dass wir von Schönheit umgeben sind – und dass wir sie mit Auge, Ohr und Verstand genießen können, sobald wir uns darauf eingestellt haben.

Nach Gold schürfen
Angesichts unserer gegenwärtigen Infotainment-Kultur hören wir nach diesem ganzen Hype um das Goldene Rechteck schon den Einpeitscher dem bezahlten Publikum im Studio zurufen: Also, Leute, ich bin restlos begeistert – ich glaube, jeder will jetzt selbst eins haben, oder? Was die Zuschauer in stürmischen Applaus ausbrechen lässt, wie es in ihren Verträgen vorgeschrieben ist. Und auch wenn Sie die teure 0190-Nummer wählen, werden Sie am anderen Ende der Leitung leider keinen eifrigen Verkäufer finden, der Ihre Bestellung für das Rechteck Ihrer Träume entgegennimmt. Trotzdem können wir die folgende materialistische Frage stellen: Gibt es ein Verfahren, mit dessen Hilfe wir unser eigenes Exemplar eines Goldenen Rechtecks konstruieren können?

Um ein perfektes Goldenes Rechteck zu konstruieren, bedient man sich eines einfachen geometrischen Verfahrens, das auf die Alten Griechen zurückgeht. Alte griechische Mathematiker (die eigentlich erst mehr als tausend Jahre nach ihrem Tod alt genannt werden) waren von der Frage fasziniert, welche geometrischen Objekte nur mit Zirkel und Lineal konstruiert werden können. Natürlich gab es damals noch kein Kabelfernsehen, sodass man sich eben mit solchen Problemen beschäftigte. Aber Spaß beiseite, Konstruktionen mit Zirkel und Lineal haben viele Menschen jahrhundertelang beschäftigt, und so wird es auch bleiben, bis längst keiner mehr von den Desperate Housewives spricht. Die meisten Leser werden eigene Erfahrungen mit solchen Konstruktionen aus ihrem Schulgeometrieunterricht haben.

Erinnern Sie sich an Ihre Jugendzeit und daran, dass die Anweisungen für klassische geometrische Konstruktionen lauten, dass das Lineal keine Maßeinheiten haben darf. Vielleicht ist diese Regel gegen Lineale ja tatsächlich angemessen, da nichts in unserer physischen Wirklichkeit wirklich genau gemessen werden kann. Wir haben ja gerade einige Kapitel zuvor festgestellt, dass zwei funktionierende Taschenrechner zwei völlig unterschiedliche Ergebnisse liefern können. Jede beliebige perfekte Messung erforderte unendlich viele übereinstimmende Ziffern – was selbstverständlich völlig unmöglich ist, wenn wir realistisch sind. Wir wollen uns daher der Herausforderung stellen, ausschließlich mit einem geraden Lineal ohne Maßeinheiten und mit einem Zirkel ein perfektes Goldenes Rechteck geometrisch zu konstruieren. Dies sind die Schritte:

Schritt i. Unsere Konstruktion beginnt mit einem perfekten Quadrat. (Bei einem gegebenen beliebigen Linienabschnitt können wir mit Zirkel und Lineal ein perfektes Quadrat konstruieren, dessen eine Seite der gegebene Linienabschnitt ist. Die beiden gleichen Werkzeuge können wir nutzen, um den genauen Mittelpunkt dieser Unterseite festzulegen. Diese Konstruktionsaufgaben möchten wir als Herausforderungen den Geometriepuristen unter unseren Lesern überlassen.) Anschließend benutzen wir das Lineal, um die untere Linie des Quadrats nach links zu verlängern, sodass wir im Endeffekt eine Figur haben, die aussieht wie ein quadratisches Haus mit einer Einfahrt auf der linken Seite (Abbildung 7.9).

Schritt 2. Als Nächstes setzen wir die gefährliche (scharfe) Spitze des Zirkels auf den Mittelpunkt der Quadratunterseite und die Bleistiftspitze des Zirkels auf die obere linke Ecke des Quadrats. Aus der gegebenen Zirkelposition heraus zeichnen wir einen Kreis, dessen Mittelpunkt sich genau in der Mitte der Quadratunterseite befindet und der durch die obere linke Ecke geht. Eigentlich brauchen wir nur einen Feil des Kreises (Abbildung 7.10).

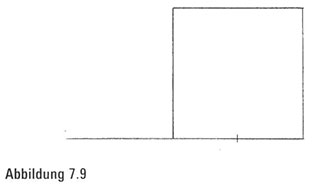
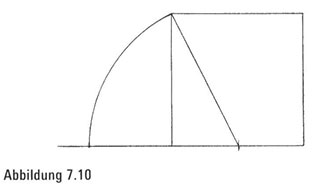
Schritt 3. Mit ähnlichen Verfahren, die wir angewandt haben, um das Ausgangsquadrat zu konstruieren, können wir eine senkrechte Linie zu unserer Einfahrt erzeugen, die durch den Schnittpunkt von Einfahrt und Kreis verläuft.

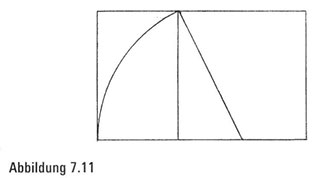
Schritt 4. Zum Schluss verlängern wir die obere Ecke des Quadrats, bis es die neue Senkrechte schneidet, sodass wir nun die überflüssigen Linien und den Kreisbogen ausradieren können (.Abbildung 7 .11).

Schauen wir uns unsere Konstruktion an. Spüren Sie eine rechtwinklige Erregung? Sollte es zutreffen, müssen Sie sich nicht dafür schämen – es ist ganz natürlich, denn wir haben gerade ein perfektes Goldenes Rechteck geschaffen. Aber ist es denn auch wirklich ein Goldenes Rechteck? Zur Bestätigung benötigen wir einen mathematischen Beweis. Wie einst John Lennon beinahe schrieb: All we are saying is give proof (Beweis) a chance. Also wollen wir es ihm zu Ehren tun.

Wertvoller Beweis
Wie beweisen wir, dass ein Rechteck ein Goldenes Rechteck ist? Wir müssen zeigen, dass das Verhältnis zwischen Grundlinie und Höhe genau dem Goldenen Schnitt entspricht, nämlich (1 + 1/5)/2. Da wir keine Maßeinheiten in unserer Abbildung haben, erklären wir einfach, dass jede Seite des Quadrats eine Länge von 2 hat. Deshalb erkennen wir sofort, dass die Höhe unseres Rechtecks 2 beträgt. Aber was ist mit der verlängerten Grundlinie? Unglücklicherweise ist deren Länge gar nicht so offensichtlich. Um diese Länge vermessen zu können, müssen wir zu Zwischenschritten in unserer Konstruktion kommen. Wenn wir die Diagonale betrachten – vor allem den Radius des Kreises, der die obere linke Ecke des Quadrats enthält, wird die grundlegende Struktur sichtbar.

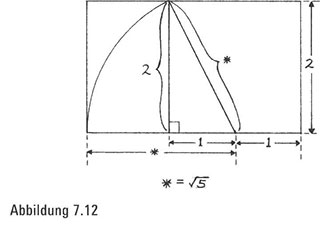
Zuerst beobachten wir, dass die Radiuslänge genau der Länge des Grundlinienabschnitts vom Mittelpunkt des Quadrats bis zum linken Ende des Rechtecks entspricht. Der verbleibende rechte Abschnitt der Grundlinie ist gleich 1, da er halb so lang ist wie die Grundlinie des Quadrats von 2X2. Deshalb betrachten wir, statt die Länge des linken Abschnitts der Rechteck-Grundlinie zu suchen, folgendes entsprechendes Problem: Wie lang ist die neue, diagonalähnliche Linie? Um das herauszufinden, stellen wir fest, dass wir mit unserer Konstruktion ein spezielles rechtwinkliges Dreieck erzeugt haben, dessen Hypotenuse unsere gesuchte Linie ist. Nun können wir leicht erkennen, dass ein Schenkel (die Grundlinie) die Länge 1 hat, während die andere (die Höhe) die Länge 2 aufweist (Abbildung 7.12).

Wenn wir jetzt den guten alten Satz des Pythagoras anwenden – das Quadrat der Hypotenuse entspricht den addierten Quadraten der Grundlinie und der Höhe -, kommen wir zu dem Ergebnis, dass die Deshalb muss die Hypotenuse eine Länge von V5 haben – ein mittlerweile vertrauter Bestandteil des Goldenen Schnitts.

Wenn wir nun noch den rechten Abschnitt der Grundlinie addieren, sehen wir, dass die genaue Länge der gesamten Grundlinie des Rechtecks

1 + 5 beträgt. Diesen Wert dividieren wir jetzt durch die Höhe
2 und entdecken, dass das Verhältnis zwischen Grundlinie und Höhe dem Wert (1 + 5)/2 entspricht. Und damit beweisen wir, dass unser Rechteck tatsächlich ein Goldenes Rechteck ist.
Der Schlüssel zu der Vorstellung hinter dieser Beweisführung ist jenes entscheidende Dreieck – ein Thema, das wir am Ende des Kapitels im Laufe eines chaotischen Endspurts noch einmal aufgreifen werden.

Von präziser Schönheit zu reinem Chaos – Glücksspiele Tipps Teil 2