Von der Papierfaltung zu Computern und flammenden Fraktalen – Lotto Tipps Teil 2

Von der Papierfaltung zu Computern und flammenden Fraktalen – Lotto Tipps Teil 1

Wenden wir uns an Turing
Hinter jedem Computer, jeder Datenübertragung, jeder Trans-aktion im Internet, jedem Computerwurm und jeder Spam-Mail, in der ein Fremder uns um Hilfe bei der legalen Überweisung von 2000000000000 Dollar auf eine amerikanische Bank bittet, steckt ein schwerschuftendes Computerprogramm. Das Programmieren, das in so vielen Bereichen unseres Lebens eine Rolle spielt, ist eigentlich eine relativ neue Kunst. Der Architekt der kreativen Kunst der Computerprogrammierung war der großartige englische Mathematiker und Computerwissenschaftler Alan Turing, der 1932 als Erster das Konzept eines Computers vorstellte. Seine Idee von der Universellen Turingmaschine führte 1950 schließlich zur Konstruktion des ersten digitalen Computers.

Turing ist bekannt für viele wichtige wissenschaftliche Beiträge. Dazu gehören seine genialen Einsichten, die die Entzifferung des Enigmacodes möglich machten, den das deutsche Militär während des Zweiten Weltkriegs in der Funkkommunikation benutzte.

Hier wollen wir nun eine Version der Turingmaschine erforschen, die als Endlicher Automat (oder auch Zustandsmaschine) bekannt ist. Grob gesagt, sind endliche Automaten die einfachsten Computer, die wir uns vorstellen können – viel einfacher als Ihr Notebook, aber mit überraschend weitreichenden Fähigkeiten.

Endliche Automaten sind äußerst einfache Maschinen. Sie lesen und schreiben lediglich Zahlen nach gewissen Regeln, die zusammengefasst besser als ein Programm bekannt sind. Stellen Sie sich das Band eines Nachrichtentickers vor, auf dem Zahlen durch eine Maschine mit einem Lese- und Schreibkopf laufen. (Natürlich denken wir dabei nicht an einen menschlichen Leser oder Schreiber.) Das Tickerband mit den Zahlen läuft durch den Lesekopf, der die Zahlen einzeln abliest. Nachdem der Lesekopf eine Zahl gelesen hat, schreibt der Schreibkopf einige Zahlen ans Ende des Tickerbands, worauf der Lesekopf darübergleitet und die nächste Zahl auf der Liste liest. Die Zahlen, die am Ende der Liste geschrieben stehen, stützen sich auf die gelesene Zahl und werden von einem speziellen Programm bestimmt. Abbildung 8.12 zeigt die grundlegende Idee.

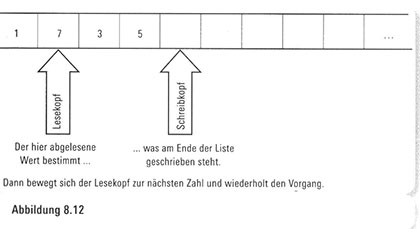
Um den Begriff des endlichen Automaten zu konkretisieren, wollen wir nun ein spezielles Beispiel geben. In diesem Programm sind die Regeln im Wesentlichen willkürlich – es gibt kein System für den Austauschwahnsinn:
Liest der Lesekopf eine 1, dann schreibt der Schreibkopf 3,2 ans Ende der Liste.
Liest der Lesekopf eine 2, dann schreibt der Schreibkopf 0,2 ans Ende der Liste.
Liest der Lesekopf eine 3, dann schreibt der Schreibkopf 3,1 ans Ende der Liste.
Liest der Lesekopf eine 4, dann schreibt der Schreibkopf 4,1 ans Ende der Liste.
Danach gleitet der Lesekopf weiter und liest die nächste Zahl auf der Liste.

Um dieses Programm auszuführen, brauchen wir mindestens eine Zahl auf unseren Tickerband. Angenommen, wir beginnen mit i. Da der Lesekopf die i liest, schreibt der Schreibkopf 3,2 ans Ende der Liste. Dann gleitet der Lesekopf weiter und liest die nächste Zahl, die 3 lautet. Nachdem der Computer diese 3 gelesen hat, schreibt er 3,1 ans Ende der Liste und liest als Nächstes die Zahl 2. Die Ausgabe sieht dann so aus:
1, 3, 2, 3, 1, o, 2, 3, 1, 3, 2.

Der Computer ist nicht gerade glücklich, wenn er die o liest, weil er keine Anweisungen hat, was er dann schreiben soll. Was macht er also? Er hält an. Wenn ein Programm stoppt, sprechen Computerwissenschaftler davon, dass das Programm anhält. Anhalten kann bedeuten, dass der Computer seinen Auftrag elegant erfüllt hat, in vielen Fällen aber ist es nur ein Euphemismus dafür, dass es abgestürzt ist. Unser Beispiel ist nicht so furchtbar kompliziert, sodass wir den Fehler im Programm gleich erkennen können, aber im Allgemeinen ist es sehr schwierig, festzustellen, ob eine Turingmaschine nach einer endlichen Zahl von Schritten anhält oder nicht.

Dieses wichtige Problem der Computerwissenschaft ist unter dem Begriff Halteprobletn bekannt. Wissenschaftler können beweisen, dass es unmöglich ist, eine allgemeingültige eiserne Regel zu ersinnen, um festzustellen, ob ein Programm anhalten wird oder nicht.

Wie sich herausstellt, lässt sich diese simple Prozedur des Lesens und Schreibens anwenden, um Computerprogramme zu schaffen, die extrem komplizierte Berechnungen ausführen können. Und in der Fat stützen sich alle Computerprogramme, wie kompliziert sie auch sein mögen – von der Textverarbeitung bis zur Internetsuchmaschine oder Onlinebanking -, auf die einfachen Lese- und Schreibregeln dieser abstrakten Turingmaschine. Die Herausforderung liegt natürlich darin, die Regeln zu ersinnen, die eine gewünschte Aufgabe ausführen. Aber statt uns Gedanken über Probleme zu machen, die Computerprogrammierern schlaflose Nächte bereiten, wollen wir einfach nur ein weiteres Beispiel endlicher Automaten betrachten. Tatsächlich werden wir uns das gerade besprochene Programm noch einmal ansehen, dieses Mal allerdings mit einer kleinen Veränderung – wir wollen die verdammte o loswerden. Und hier sind die neuen Regeln für unsere Maschine.

Liest der Lesekopf eine 1, dann schreibt der Schreibkopf 3,2 ans Ende der Liste.
Liest der Lesekopf eine 2, dann schreibt der Schreibkopf 4,2 ans Ende der Liste.
Liest der Lesekopf eine 3, dann schreibt der Schreibkopf 3,1 ans Ende der Liste.
Liest der Lesekopf eine 4, dann schreibt der Schreibkopf 4,1 ans Ende der Liste.
Oanach gleitet der Lesekopf weiter und liest die nächste Zahl auf der Liste.

Starten wir nun dieses Programm, wenn auf dem Tickerband die i steht, lässt sich leicht erkennen, dass dieses Programm niemals anhalten wird, da jeder vom Schreibkopf geschriebene Wert (1,2,3 oder 4) ein zulässiger Wert ist, den der Lesekopf lesen kann. Folglich wird dieses Programm ewig laufen und eine endlose Ziffernliste ausspucken. Angenommen, 1 wäre die Startzahl, dann erzeugt der Computer eine Reihe, die folgendermaßen anfängt:
1, 3, 2, 3, 1, 4, 2, 3, 1, 3, 2, 4, 1, 4, 2, 3, 1 ….

Vielleicht sollten wir nicht allzu beeindruckt sein. Es scheint, als erzeuge dieses einfache Programm eine langweilige Zufallsliste unendlich vieler Zahlen. Aber bevor wir weitermachen, sollten wir die Liste vereinfachen, indem wir feststellen, ob die Zahlen gerade oder ungerade sind. Wir ersetzen also jede ungerade Zahl durch ein seltsames Symbol – sagen wir V – und tauschen jede gerade Zahl durch ein noch seltsameres Symbol – sagen wir A – aus. Ersetzen wir nun die Ausgabeziffern durch diese Symbole, erhalten wir diese Reihe:

In einer unglaublichen Wende der Ereignisse stellt sich heraus, dass wir dabei genau unsere Papierfaltungssequenz für beliebig viele Faltungen erzeugen! Demnach ist die Papierfaltungssequenz in Wirklichkeit das Ergebnis eines äußerst einfachen, aus fünf Zeilen bestehenden Turingmaschinenprogramms. Was vielleicht noch erstaunlicher ist: Wir brauchen die letzte Faltungssequenz nicht mehr, um die nächste zu bestimmen. Mit den fünf Regeln und dem Ausgangssamenkorn i können wir uns durch diese Bügelfalten bewegen und die Papierfaltungssequenz für beliebig viele Faltungen erzeugen.

Die frühen Terme in der Folge erzeugen auf natürliche Weise die folgenden Terme, bis die Liste nach 51 Faltungen so lang ist, dass sie weit über die Sonne hinausgeht. Es ist schon erstaunlich, dass allein diese fünf einfachen Regeln eine perfekte Faltungsprozedur für jeden beliebigen Kurs erzeugen, den wir einschlagen möchten. In den wellenförmigen Auf-und-ab-Bewegungen auf unserem Papier ist die ganze künftige Faltungsgeschichte enthalten – unzählige Kilometer entfernt an einem Horizont, den wir nie erreichen werden. Dieser chaotische Faltungswirrwarr hat in der Tat mehr Struktur, als wir auf den ersten Blick wahrnehmen können.

Von gefalteten Schwanen zu gefalteten Drachen
Wir geben zu, dass wir nach all diesen Seiten keinen Fortschritt in der Kunst gemacht haben, einen Origami-Schwan zum Leben zu erwecken. In der Hoffnung, dem Geflügelproblem auszuweichen, lassen wir den zierlichen, kleinen Schwan links liegen und initiieren ein zündendes Verfahren, um ein Stück Papier in einen feurigen Drachen zu falten. Unsere Drachengeschichte birgt sowohl gute als auch schlechte Nachrichten. Einerseits müssen Sie für unser Verfahren überhaupt keine Origami-Technik beherrschen – wir werden ganz einfach unsere banale Faltung von rechts nach links anwenden, die zur wichtigsten Stütze der gesamten Erörterung geworden ist. Wie wir jedoch sehen werden, gibt es auch eine dunkle Seite.

Unsere Papierfaltungssequenz ergab sich daraus, dass wir das Papier einige Male von rechts nach links gefaltet haben und es dann vorsichtig wieder entfaltet haben. Wir haben die Täler und Kämme gezählt, die durchs Falten entstanden sind, und haben unsere Sequenz aufgeschrieben. Jetzt kehren wir zu den Bügelfalten im Papier zurück und fragen uns, welche Form wir sähen, wenn wir das Papier so arrangierten, dass jede Faltung einen Winkel von 90 Grad bildete? Eine einzige Faltung ergibt auch einen einzigen 90-Grad-Winkel (Abbildung 8.13). Passen wir das Papier nach zwei Faltungen so an, dass alle Winkel rechte Winkel sind, haben wir

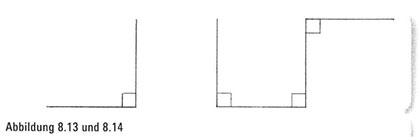
es mit einem Bild zu tun, das einer Stielkasserolle ähnelt (Abbildung 8.14).
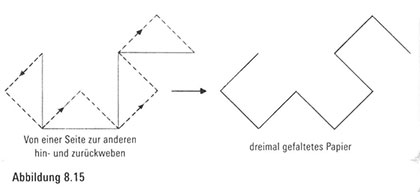
Können wir, beginnend mit dem zweimal gefalteten Bild, das dreifach gefaltete Vorhersagen? Die Antwort heißt ja – und wir wissen auch bereits, wie es funktioniert. Wir erinnern uns, dass eine Methode zur Erzeugung der nächsten Papierfaltungsgeneration darin besteht, die Tal-Kamm-Sequenz wellenförmig in die aktuelle Sequenz hineinzuweben. Hier können wir diese Prozedur visuell anwenden, indem wir eine Sequenz abwechselnder Rauf- und-runter-Faltungen zwischen die Falten unserer rechtwinkligen Arrangements einfügen (Abbildung 8.15).

Bei der nächsten Faltung kommt eine noch exotischere Form zum Vorschein (Abbildung 8.16). Dieses Bild müsste aufmerksamen Lesern von Michael Crichtons Roman Jurassic Park von 1990 vertraut Vorkommen. Die Geschichte ist nämlich in Abschnitte aufgeteilt, die Iterationen genannt werden. Jede beginnt mit einem Zitat der fiktiven Person Ian Malcolm. Beigefügt ist ein Bild, das als Metapher für die zunehmende Komplexität der Handlung zu verstehen ist. Zur ersten Iteration gehört das Bild von Abbildung 8.16 sowie das Zitat Bei der ersten Darstellung der Fraktal- kurve zeigen sich nur wenige Hinweise auf die zugrunde liegende

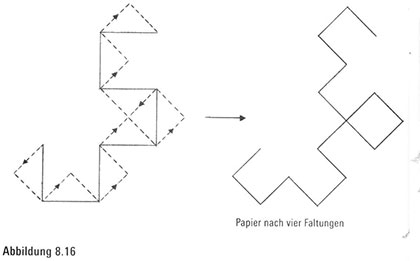
mathematische Struktur. Jetzt erkennen wir, dass dieses Icon nichts anderes ist als einer von vielen Schritten in unserem entfalteten und rechtwinklig angeordneten Papierfaltungsprozess – ein äußerst angemessenes Bild, da wir die Schritte des Papierfaltens als Iterationen eines einfachen Prozesses betrachten können.
Crichtons zweite Iteration enthält das Bild einer Papierfaltungssequenz mit einer zusätzlichen Faltung, erneut in rechtwinkliger Anordnung (Abbildung 8.ij). Hier erläutert Ian:

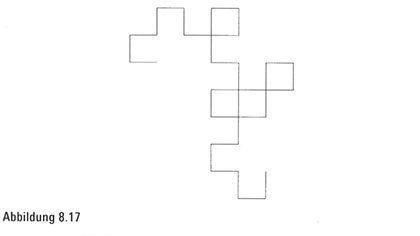
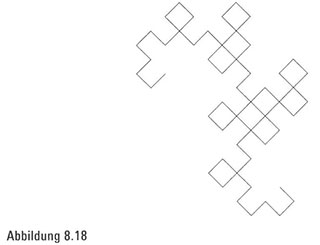
Bei nachfolgenden Darstellungen des Fraktals können plötzliche Veränderungen auftreten. Die dritte Iteration (Abbildung 8.18), die auch die nächste Iteration der Papierfaltungskurve ist, enthält eine Anzahl Quadrate.

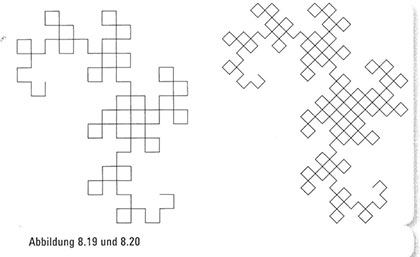
An diesen Punkten schneiden sich die Winkel des Papiers. Bei nachfolgenden Darstellungen treten Details deutlicher zutage, ruft Ian aus. Und während die Geschichte von Jurassic Park sich entfaltet, werden auch die Bilder komplizierter, sodass Ians Ausrufe zunehmend düsterer werden: Unweigerlich kommen mit der Zeit zugrunde liegende Instabilitäten zum Vorschein (die vierte Iteration, Abbildung 8.19); Fehler im System zeigen jetzt schwerwiegende Folgen (die fünfte, Abbildung 8.20)-, Eine Wiederherstellung des Systems kann sich als unmöglich er-weisen (die sechste, Abbildung 8.21), und bei der siebten Iteration (Abbildung 8.22) heißt es schließlich: Je weiter die Berechnungen fortschreiten, desto mehr Mut gehört dazu, sich ihren Implikationen zu stellen.

Es gibt natürlich keinen Zweifel: Das in den Mittelpunkt unserer Aufmerksamkeit rückende Bild der Papierfaltung ist kein geringeres als das der feurigen Drachenkurve, der wir erstmals zu Beginn dieses Kapitels begegneten. Bei dieser ersten Auseinandersetzung

nahmen wir an, das erforderliche Verfahren zur Erzeugung eines solch unendlich komplizierten Objekts ginge weit über unsere mathematischen Fähigkeiten hinaus. Inzwischen jedoch erkennen wir nach unserer Reise durch die Welt der Faltungen, dass unser feuerspeiendes Ungeheuer in Wirklichkeit das Ergebnis eines extrem einfachen Prozesses ist, nämlich der Faltung eines Papiers von rechts nach links.

Die Drachenkurve ist das Endresultat unendlich vieler Faltungen. Folglich erkennen wir die dunkle Seite der Drachenkurve – um eine perfekte Kurve zu erschaffen, müssen wir die banale Aufgabe des Faltens unendlich oft wiederholen. Natürlich haben wir in unsere Turingmaschine diese endlosen Anweisungen eingebaut, aber die Ausführung dieser endlosen Schritte nähme mehr als ein lebenslanges Bemühen in Anspruch. Auf der Sonnenseite hingegen erkennen wir, dass das zunächst unverständlich Erscheinende durch die einfache Suche nach Mustern und Strukturen glasklar werden kann.

Wie Sie vielleicht bei einigen von Ian Malcolms Kommentaren bereits vermutet haben, ist die Drachenkurve ein Beispiel für ein Fraktal.

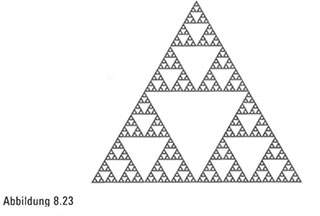
Ein Fraktal ist jedes beliebige geometrische Objekt, das unendliche Komplexität aufweist. Ganz häufig sind Fraktale selbstähnlicher Natur, wobei ein vergrößerter Teil dem gesamten Objekt ähnelt (Abbildung 8.23). In vielen Fällen wird ein fraktales Bild durch einen simplen Prozess erzeugt, der ständig wiederholt wird. Deshalb kommt in der Drachenkurve auch der fraktale Sinn so schön zum Ausdruck.

Drachen von einer Wand zur anderen
Auf unserer verrückten, intellektuellen Reise haben wir anfangs Papiere gefaltet, haben dann Muster und einfache Computerprogramme entdeckt, bis wir schließlich feuerspeiende Drachen fanden. Wir wollen diese Reise nun mit einer letzten Überraschung beenden. Da die Drachenkurve durch das unendlich wiederholte Knicken von Papier entsteht, weist sie auch eine unendlich gezackte Grenze auf. Ihre krause Haut besteht aus unendlich vielen Falten. Die unendlich zerknitterte Haut des Drachens hat völlig unerwartet eine narzisstische Selbstbezüglichkeit. Das heißt, wenn wir die Drachenkurve ein paarmal kopieren und die daraus entstehenden Kopien als Puzzleteile betrachten, passen sie perfekt ineinander und bedecken die gesamte Fläche (Abbildung 8.24)! Die Erkenntnis, dass der Umriss der Drachenkurvenhaut perfekt zu den anderen Kopien ihrer selbst passt, ist ein weiterer Beweis für die scheinbar endlose Strukturmenge, die der einfache Papierfaltungsprozess in sich birgt. Zusätzlich bietet dieses Verfahren eine weitere Kachelung der Fläche an, bei der wir lediglich einen Kacheltyp benötigen. Später lernten wir eine Parkettierungsmethode kennen, bei der wir Goldene Dreiecke verwendeten. Durch das Verkacheln mit Goldenen Dreiecken und mit der Drachenkurve erschaffen ein begriffliches Yin und Yang der Einfachheit und Komplexität.

Die Goldenen Dreiecke sind äußerst einfache Kacheln, aber sie können so zusammengelegt werden, dass sie auf der Fläche ein chaotisches Muster ergeben, das unendlich kompliziert ist und sich nie wiederholt. Hier haben wir Drachenkurvenkacheln gefunden, die unendlich kompliziert sind, aber auf periodische Weise zusammenpassen – das heißt, sie wiederholen sich in regelmäßigen Abständen.

Beim einfachen Falten eines Papierbogens haben wir wunderschöne Muster entdeckt, sind zu Zeugen der Geburt der modernen Computerwissenschaft geworden und haben die unendliche Komplexität der Drachenkurvenfraktale gezähmt. Und, was noch wichtiger ist: wir haben entdeckt, welche Erfolge die Suche nach Strukturen zeitigt. Die Suche nach Strukturen ist eigentlich eine Annäherung an das Verstehen – eine Reise, die uns zunächst in ferne Welten führt, dann aber über Irrungen und Wirrungen, Kräuselungen und Faltungen zurück in unsere eigene Welt zurückbringt. Im nächsten Kapitel treiben wir die Irrungen und Wirrungen auf den Höhepunkt und entdecken dabei Welten, die fremdartig und vertraut zugleich wirken.