Von der Papierfaltung zu Computern und flammenden Fraktalen – Lotto Tipps Teil 1

Not chaos like together crushes and bruised,
But, as the world harmonious/y confused:
Where order in variety we see,
And where, though all things differ, all agree.
Alexander Pope

Offensichtlich … Das Verfahren zur Erzeugung des unendlich komplexen Bildes, das als die Drachenkurve bekannt ist (Abbildung 8.1), erfordert unendlich komplexe Mathematik.

Überraschung … Das Verfahren erfordert lediglich die hirnlose Arbeit, ein Blatt Papier zu falten. Der einzige Kniff dabei ist, dass wir diese Aufgabe unendlich oft wiederholen müssten. Wenn wir in einfachen Vergnügungen Muster suchen, drängen sich uns verborgene Strukturen auf – in diesem Fall werden wir mit der feurigen Drachenkurve konfrontiert. Erstaunlicherweise kann man mit dieser zerfurchten Kurve den Fußboden ohne Lücken und Überlappungen pflastern! Darüber hinaus finden wir in den Faltungen unseres Papierblatts die Grundlagen des modernen Rechnens.

Wir wollen aufrichtig sein – im Leben werden wir ständig mit Umständen konfrontiert, die furchtbar kompliziert und scheinbar unüberwindlich sind. Manchmal ist unser erster Eindruck, dass die Situation hoffnungslos ist und nur Magengeschwüre verursacht. In diesem Kapitel werden wir eine Reise durch die faszinierenden Höhen und Tiefen des Papierfaltens als Metapher für die Entwirrung der Kompliziertheit des Lebens benutzen. Wir wünschen uns, dass diese Reise den Hoffnungslosen Zuversicht und den Nervösen Ruhe bringen möge.

Unser Hauptziel ist die Annahme der Erkenntnis, dass wir komplizierte Phänomene verstehen können, indem wir einfache Fälle auf tiefgründige Art und Weise betrachten. Mit dem Verfahren, ein Stück Papier wiederholt zu falten, werden wir entdecken, dass Objekte und Probleme, die zunächst völlig chaotisch und zusammenhanglos zu sein scheinen, in Wirklichkeit wunderschöne Strukturen besitzen, die zu großartigen Verbindungen zwischen unterschiedlichen Begriffen führen. Also greifen wir zu einem Stück Papier und schauen uns an, was sich da entfalten wird.

Einarbeiten ins Falten
Wir beginnen mit einem Blatt Papier und dem denkbar einfachsten Vorgang: Wir falten es in der Mitte und klappen die rechte Seite auf die linke (Abbildung 8.2). Selbst diejenigen unter uns, für die Origami eine Herausforderung ist (und die nicht in der Lage sind, ein Stück Papier in einen anmutigen Schwan zu verwandeln), können dieses Manöver ausführen.

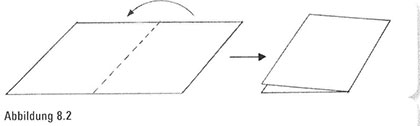
Allerdings sind wir mit dieser einen Faltung noch nicht zufrieden. Stattdessen falten wir unser gefaltetes Papier noch einmal – rechts über links (.Abbildung 8.3).

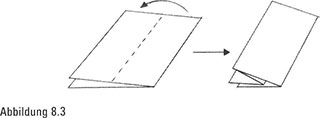
Damit hören wir aber nicht auf – oder sollten wir? Versuchen Sie es selbst. Wie oft können Sie das Papier falten?

Wie wir bereits in Kapitel 5 gesehen haben, ist die Dicke eines Papierblatts zwar gering, aber nicht null. Könnten wir das Papier zweiundvierzigmal falten, würde es von unserem Schreibtisch bis zum Mond reichen. Stattdessen falten wir es einfach so oft, wie wir es gerade schaffen (fünf- oder sechsmal) und falten es dann wieder auseinander, um zu sehen, was wir da erschaffen haben. Wir möchten Sie eindringlich bitten, diese wagemutigen, wiederholten Faltungen von rechts auf links gemeinsam mit uns durchzuführen.

Wenn wir das Papier auseinanderfalten, nachdem wir so viele Faltungen wie möglich durchgeführt haben, erkennen wir ein krauses Durcheinander, ohne jede Struktur. Sobald wir den ersten Schrecken über das zerknitterte Chaos überwunden haben, schauen wir etwas genauer hin und machen eine banale Entdeckung: Die Faltungen tauchen in zwei Kategorien auf: nach oben und nach unten weisende. Die nach unten zeigenden Faltungen wollen wir Täler nennen und durch das Symbol V darstellen, während wir die spitz nach oben zulaufenden Faltungen als Kämme bezeichnen wollen, denen wir das Symbol A zuordnen.

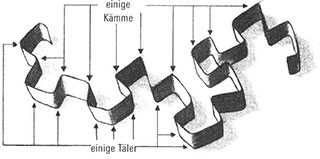
Abbildung 8.4: Der bloße Akt des Benennens von Objekten trägt häufig dazu bei, dass wir sie besser verstehen.

Wenn wir die Falten des gefalteten Papiers in Abbildung 8.4 von links nach rechts lesen, erkennen wir eine Sequenz, die folgendermaßen beginnt:

Tal Tal Kamm Tal Tal Kamm Kamm …
Wenn wir nun diese Folge von Tälern und Kämmen betrachten, fällt uns noch kein wahrnehmbares Muster auf. Aber warum nicht? Immerhin sind wir unsere Faltung ganz systematisch angegangen und haben immer von rechts nach links geknickt. Also haben wir auch erwartet, dass die einheitlichen Wiederholungen irgendeine Art von Muster ergeben und nicht dieses komplizierte Durcheinander. Aber wenn wir mit Komplexität konfrontiert sind, sollten wir auf die bewährte Strategie zurückgreifen, uns abzuwenden und mit etwas Einfachem neu anzufangen. In diesem Fall ist die Ursache der Komplikation eindeutig: so viele blöde Faltungen! Also fangen wir mit einer sauberen Tafel oder, genauer gesagt, mit einem sauberen Blatt Papier an und unterdrücken dieses Mal unseren Wunsch, es ungehindert zu knicken.

Ein paar gute Faltungen
Wenn wir das Papier nur einmal falten und es dann wieder öffnen, (Abbildung 8.5), sehen wir ein einsames Tal – so weit, so gut. Falten wir es zweimal (Abbildung 8.6), sehen wir zwei Täler, gefolgt von einem einsamen Kamm. Wenn wir das Blatt dreimal knicken (Abbildung 8.7), kommen folgende Bügelfalten zum Vorschein:
Tal Tal Kamm Tal Tal Kamm Kamm

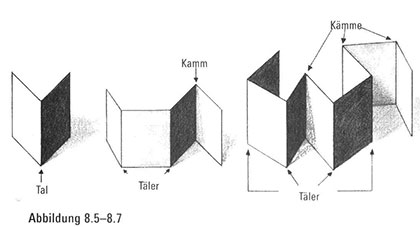
Wenn wir nun diese Papierfaltungsfolgen auflisten und sie als Ganzes betrachten, stoßen wir ganz von selbst auf eine sich abzeichnende Überraschung:
Tal
Tal Tal Kamm
Tal Tal Kamm Tal Tal Kamm Kamm

Ein Muster entsteht. Der erste Teil jeder neuen Sequenz gleicht haargenau der darüberstehenden Sequenz. Um diese Beobachtung zu bestätigen, wollen wir noch eine Faltung machen. Dieses Mal knicken wir das Blatt viermal, bevor wir es auseinanderfalten (.Abbildung 8.8). Das Resultat fügen wir ans Ende unserer voausgegangenen Liste an und sparen Platz, indem wir unsere Symbole V und A benutzen, statt die Worte Tal und Kamm auszuschreiben:

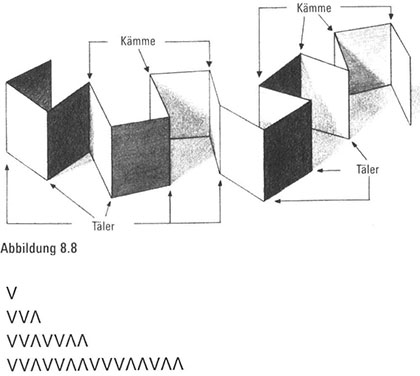
Und tatsächlich setzt sich das überraschende Muster fort, wenn wir das Papier fünf- oder sechsmal falten. Wir erkennen, dass der erste Teil der fünffachen Folge mit der vierfachen Folge übereinstimmt und der erste Teil der sechsfachen Folge der fünffachen Sequenz gleicht.

Diese Beobachtung führt uns zu der Erkenntnis, die erste Hälfte der Papierfaltungssequenz für jede beliebige Anzahl von Faltungen voraussagen zu können, einfach weil wir die Faltungssequenz für die unmittelbar vorausgegangene Faltung kennen. Wenn wir die Faltungen mit Symbolen darstellen und die Sequenzen aufzeichnen, entstehen bestimmte Muster. Haben wir erst einmal eine Struktur gefunden, können wir nicht umhin, weiterzusuchen. In diesem Fall fangen wir mit dem Versuch an, den mittleren Term in der Folge vorauszusagen. Wir haben in jeder folgenden Reihe den in der Mitte stehenden Term unterstrichen.

Erneut erkennen wir eine verblüffende Übereinstimmung. Jeder mittlere Term ist ein V. Wie können wir jetzt die zweite Hälfte der Sequenz Vorhersagen? Die Täler und Kämme in dieser Sequenz entstanden auf natürliche Art und Weise aus dem Verfahren, ein Stück Papier von rechts nach links zu falten. Also fragt man sich ganz von selbst, was geschähe, wenn wir eine der Symbolfolgen durch das V in der Mitte falteten – das heißt, wenn wir die rechte Hälfte der Sequenz über die linke Hälfte der Sequenz drehen würden, so als wäre sie über ein Scharnier mit dem mittleren V verbunden (Abbildung 8.9).

Überraschung. Wenn wir die rechte Hälfte der Sequenz auf die linke Hälfte drehen, dann stimmen diese beiden Hälften genau überein. Wenn wir also beispielsweise die rechte Hälfte der Sequenz VVA – nämlich A – drehen, verwandelt es sich in V und stimmt mit dem linken V überein (Abbildung 8.10). Etwas Ähnliches geschieht, wenn wir VV/VV// in der Mitte falten, da die rechten Terme VAA sich nach der Drehung in WA verwandeln und daher mit der linken Hälfte von WAV VAA (Abbildung 8.11) identisch sind.

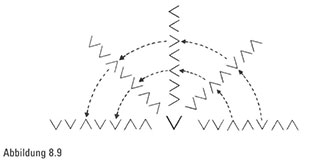
Diese Symmetrie der Übereinstimmung nach der Faltung bleibt während der gesamten Faltsequenz erhalten.

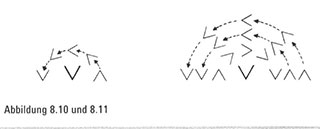
Wir sind daher in der Lage, die Papierfaltungssequenz für sieben Faltungen zu erzeugen. Dafür schreiben wir die Folge für sechs Faltungen auf, hängen ein zusätzliches V an (das gleich zum neuen Mittelpunkt-V wird) und drehen dann die Sechsersequenz über das neu hinzugefügte V , als sei sie mit dem V durch ein Scharnier verbunden. Das Ergebnis ist eine beeindruckend lange Reihe:

Kein Chaos mehr
Wir haben gerade das Chaos gezähmt. Jetzt können wir die Papierfaltungssequenz auf jede beliebige Anzahl von Faltungen anwenden – selbst auf solche Faltungen, die physikalisch unmöglich sind. Insofern erlaubt uns unsere Entdeckung, tatsächlich die Beschränkungen unserer materiellen Welt und des Papiers zu überwinden. Obwohl wir ein Papier in Wirklichkeit nur siebenmal falten können, wissen wir jetzt, wie wir das richtige Faltungsmuster für ein Papier erzeugen können, das theoretisch achtmal gefaltet worden ist. Wir schreiben einfach die Siebenersequenz hin, fügen ein V hinzu und klappen dann die Siebenersequenz über das in der Mitte stehende V und erzeugen so die zweite Hälfte der Achtersequenz. Theoretisch könnten wir die Prozedur bis zur 5ier-Sequenz und darüber hinaus fortsetzen. Aber mit dieser langen Kette aus Vs und As würden wir dann natürlich nicht nur knapp, sondern weit über die Sonne hinausschießen.

All diese neuen Einsichten ergaben sich aus der einfachen Benennung der Täler und Kämme, die wir sahen, und aus der Suche nach einem Muster. Plötzlich war das Bügelfalten-Chaos kristallklar geworden.

Vom reinen Chaos zur vollständigen Regelmäßigkeit
Und jetzt geht es um etwas ganz anderes. Erforschen wir die Papierfaltungssequenz aus einem anderen Blickwinkel, entdecken wir plötzlich ein einfaches Muster, das in den Faltungen verborgen ist und uns erlaubt, die neuen Sequenzen auf völlig neue Art und Weise zu erzeugen. Als ersten Schritt schreiben wir die Papierfaltungssequenzen zur Mitte ausgerichtet hin (wobei das mittlere V in der Mitte der Reihe steht). Konzentrieren wir uns dann auf jeden weiteren Term und fangen mit den ersten an (die fettgedruckt sind), sehen wir etwas ganz und gar Unerwartetes:

Die fettgedruckten Terme weisen eine unvergleichliche Regel-mäßigkeit auf. Sie wechseln sich tatsächlich ab – Tal, Kamm, Tal, Kamm und so weiter:

Konzentrieren wir uns jetzt auf die nicht fettgedruckten Terme, rückt etwas wirklich Bemerkenswertes in den Brennpunkt unserer Aufmerksamkeit. Betrachten wir beispielsweise die Folge der Viererfaltung:

Wenn wir jetzt die fettgedruckten, alternierenden Terme entfernen, kommt folgende Sequenz zum Vorschein:

Sie müsste uns vertraut Vorkommen. Erkennen Sie sie? Sie entspricht genau der Sequenz der Dreifachfaltung! Wenn wir ein paar weitere Sequenzen überprüfen, werden wir sehen, dass das Gleiche geschieht: Nach der Entfernung der alternierenden Terme aus jeder beliebigen Papierfaltungssequenz bleibt genau die vorausgegangene Papierfaltungssequenz übrig. Folglich sehen wir ein überraschendes, in gewisser Weise inzestuöses Verhalten unter diesen Abfolgen von Tälern und Kämmen.

Diese phantastische Struktur können wir zur Erzeugung neuer Papierfaltungssequenzen nutzen, indem wir Terme einfügen. Für jede beliebige Papierfaltungsfolge können wir die nächste Folge konstruieren, indem wir einfach die vorhandene Folge nehmen, zwischen den aufeinanderfolgenden Termen Platz lassen und dann eine Reihe alternierender Täler und Kämme hineinweben. Gegeben sei beispielsweise die Dreifaltigkeitssequenz VVAVVAA. Die Vierfachfaltung erhalten wir durch Separierung der Terme und indem wir die Auf-und-ab-Sequenz hineinweben, sodass ein Mix entsteht:

Wir haben also zwei unterschiedliche verborgene Muster entdeckt, die es uns gestatten, die Papierfaltungssequenz auf zweifache Weise zu erzeugen. Unser erstes Verfahren, die nächste Faltungssequenz zu erzeugen, beginnt damit, dass wir die vorausgegangene Sequenz nehmen, ein V hinzufügen und dann eine Kopie der Sequenz über das V in der Mitte auf die andere Seite klappen. Die zweite Möglichkeit, die gleiche Folge zu erzeugen, besteht darin, die vorausgegangene Faltungssequenz zu nehmen, sie so auszubreiten, dass Lücken entstehen, und diese mit der einfachen Auf-und-ab-Sequenz (Tal, Kamm, Tal, Kamm) zu füllen.

Obwohl wir das ursprüngliche vermeintliche Chaos gezähmt haben, leiden beide Erzeugungsprozesse an einem anscheinend notwendigen Übel: Beide verlangen, dass wir die vorausgegangene Faltungssequenz kennen, um die nächste bestimmen zu können. Offenbar müssen wir also, um das Papier sechsmal zu falten, es auf jeden Fall fünfmal falten, sodass es gewissermaßen natürlich erscheint, dass die fünffältige Sequenz in die Faltung eingebunden werden muss, bevor wir zur sechsfältigen Sequenz kommen. Natürlich schon, aber ist es auch notwendig? Die Antwort auf diese Frage bietet eine wunderbare Möglichkeit, Vorstellungen in Betracht zu ziehen, die zu den Ecksteinen des gegenwärtigen Computerzeitalters gehören.

Von der Papierfaltung zu Computern und flammenden Fraktalen – Lotto Tipps Teil 2