Eine Reise in die Unendlichkeit – Lotto und Glücksspiele Tipps Teil 1

O Gott, ich könnte in eine Nußschale eingesperrt sein und mich für einen König von unermeßlichem Gebiete halten.
William Shakespeare

Offensichtlich … Wir werfen zehn Tischtennisbälle in eine Tonne; dann langen wir hinein, greifen uns einen und werfen ihn hinaus. Wir müssen keine Raketeningenieure sein, um zu erkennen, dass jetzt noch neun Bälle im Fass liegen. Jetzt werfen wir noch einmal zehn Bälle hinein und nehmen wieder einen heraus. Selbst diejenigen unter uns, die Mengenlehre in der Schule hatten, werden zustimmen, dass noch 18 Bälle im Fass liegen. Wiederholen Sie den Vorgang, und wir haben noch 27 Bälle übrig, nach der nächsten Runde haben wir dann 36, danach 45 und so weiter. Wir erkennen das Muster. Was aber geschähe, wenn wir dieses Spiel ewig fortsetzten?

Überraschung… Das Fass würde leer werden. Willkommen in der unglaublichen und der Intuition zuwiderlaufenden Welt des Unendlichen.

Für die meisten von uns beginnt die Unendlichkeit im Alltagsleben mit dem Gedanken an Bill Gates’ sagenhaften Reichtum. Selbst das Wort Unendlichkeit ruft ein großes Gefühl von majestätischer Weite, Geheimnis und Unbegreiflichkeit hervor. Während des größten Teils der bekannten Geschichte kamen die Menschen nicht über die Anschauung hinaus, die Unendlichkeit sei ein verschwommenes, einschüchterndes Rätsel, ein gottähnliches, allumfassendes Ganzes, unerkennbar und unvorstellbar. Zwar ließ sich nichts Vernünftiges darüber sagen, aber immerhin kam man darin überein, dass die Unendlichkeit sehr groß sei. In der Tat einigte man sich darauf, die Unendlichkeit sei nun mal so groß, wie sie wird. So arrangierte man sich – aber man lag falsch.

Wie sich herausstellt und wie wir in diesen beiden letzten Kapiteln noch entdecken werden, macht es durchaus Sinn, bis ins Unendliche weiterzuzählen – und noch darüber hinaus. Wir werden nämlich erkennen, dass das Thema Unendlichkeit nicht so schwierig ist, wie zwei gleiche Socken im Wäschetrockner zu finden, denn das Unendliche hat nichts mit Festklammern und Stehenbleiben zu tun. Obwohl die Reise in die Unendlichkeit nicht schwierig ist, wird sie uns Offenbarungen und Einsichten vermitteln, die unserer Intuition zuwiderlaufen.

Nicht zu ermittelnde Zahlen
Die ganze Idee der Unendlichkeit läuft darauf hinaus, dass sie größer ist als alle Zahlen. Sie liegt mit Gewissheit jenseits der 14, lässt auch die 2343 hinter sich und selbst die 1 234826. Tatsächlich ist sie noch viel größer als 14736030038738574387983475937984 794 357 398 753- Und in der Tat ist diese riesige Zahl nicht einmal eine winzige Schuppe auf der Kopfhaut eines Wals.

Bevor wir nun das einschüchternde Konzept der Unendlichkeit
kennenlernen, wollen wir zuerst eine einfacher erscheinende Frage diskutieren. Können wir die vertrauten natürlichen Zahlen, also 1, 2,3,4… verstehen? Alles kein Problem, bis wir diese drei kleinen Punkte hinter der 4 sehen, weil uns die Auslassungszeichen zu verstehen geben, dass wir unendlich lange weiterzählen müssen, und unendlich lange ist eine außerordentlich lange Zeit. Wie wir bereits in Kapitel 4 gesehen haben, begreifen wir die Bedeutung von 1, 2 und 3. Die 2 verstehen wir, weil wir überall Paare entdecken können: Sockenpaare, Würfelpaare, Zwillingspaare. Auf ähnliche Weise erfassen wir die 3 aufgrund uns geläufiger Mengen intuitiv – Tennisbälle in der Dose oder die Räder eines Dreirads. Was die 4 betrifft, so ist dies die Zahl von Bridgespielern, der Wände eines normalen Zimmers oder der Radkappen eines Autos, das in einer Wohngegend mit niedriger Kriminalitätsrate geparkt wird. Doch während die Zahlen immer größer werden, schwindet gleichzeitig unser intuitives Gefühl für sie.

Wie wir schon erfahren haben, besteht die Zahl des amerikanischen Haushaltsdefizits aus 13 Ziffern. Konkret beliefen sich die Staatsschulden am 11. Januar 2003 auf 6 420 664 216 307 Dollar. Das lässt sich in Worte fassen: Heiliger Strohsack! zum Beispiel oder, genauer formuliert: 6 Billionen 420 Milliarden … und so weiter. Es fällt schwer, die Bedeutung dieser enormen Größe zu begreifen.

Astronomen schätzen, dass die Gesamtzahl der Atome im Universum mit 80 Ziffern ausgedrückt werden könnten – aber haben denn solche spektakulär großen Zahlen irgendeine persönliche Bedeutung für uns? Wie wär’s mit einer tausendstelligen Zahl? Wie machen sich eine Million Ziffern? Zahlen mit einer Million Stellen sind im Wesentlichen bedeutungslos, und dennoch sind die meisten Zahlen, die es gibt, noch größer. Lange bevor wir zur Unendlichkeit gelangen, müssen wir uns mit Vorstellungen jenseits unseres Auffassungsvermögens befassen.

Zahlen, die die Zahl der Teilchen im uns vertrauten Universum überschreiten, lassen sich unserer Intuition nicht begreiflich machen. Wie können wir angesichts dieser Gedanken jemals hoffen, das Unendliche zu verstehen? Wie schon Woody Allen lamentierte: Ich staune immer über Leute, die glauben, das Universum zu , wo es doch schon schwer genug ist, sich in Chinatown auszukennen.

Nah dran an der Unendlichkeit
Glücklicherweise liegt, wie wir gleich entdecken werden, der Aufstieg zur Unendlichkeit sehr wohl im Bereich unserer Bergsteigerfähigkeiten. Tatsächlich lautet die erste Überraschung, die uns in diesem Zusammenhang begegnet, dass die Unendlichkeit wahrhaftig einen Sinn ergeben kann. Unsere Strategie besteht darin, uns von hochtrabenden Konzepten zu distanzieren, zu deren Umsetzung wir nicht in der Lage sind, und stattdessen ganz behutsam über einfache und vertraute Dinge nachzudenken. Normalerweise machen wir kehrt und laufen weg, wenn wir vor einer großen Herausforderung stehen. In diesem Fall sollten wir versuchen, die 5 zu verstehen, statt gleich mit der Unendlichkeit zu beginnen. Denn das ist eine Größe, mit der wir vermutlich umgehen können, zumal es die Zahl der Finger an den Händen der allermeisten Menschen ist.

Die entscheidende Beobachtung rückt in den Brennpunktunserer Aufmerksamkeit, wenn wir Musterbeispiele derselben Zahl in Augenschein nehmen. Im Fall der 5 sind die Finger der linken Hand ein Beispiel und die Finger der rechten Hand ein anderes. Legen wir zuerst die Spitze unseres linken kleinen Fingers auf die Spitze unseres rechten kleinen Fingers und lassen dann unsere Ringfinger einander berühren, danach die Mittelfinger, Zeigefinger und
schließlich unsere Daumen (Abbildung 11.1). Was wir hier sehen, ist eine Korrespondenz – eine Eins-zu-eins-Entsprechung – zwischen den Fingern unserer linken Hand und den Fingern unserer rechten Hand. Selbst wenn wir nicht bis 5 zählen könnten, wüssten wir mit Sicherheit, dass die Zahl der Finger unserer linken Hand der Zahl der Finger unserer rechten Hand entspricht.

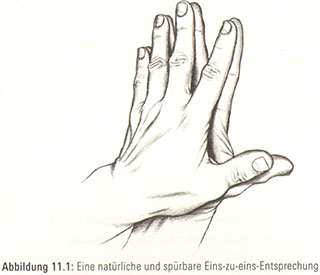
Jetzt haben wir ein neues Gefühl für die 5. Fünf ist die Größe jeder Menge von Objekten, die genau mit den Fingern jeder beliebigen linken Hand in Übereinstimmung gebracht werden kann. Folglich ist die Anzahl i-Cent-Münzen, die erforderlich ist, um dem Wert einer 5-Cent-Münze zu entsprechen, 5, da wir auf jeder Fingerspitze unserer linken Hand eine i-Cent-Münze balancieren können, ohne dass eine Münze oder ein kleiner Finger übrig bleibt. Folgende natürliche und einfache Vorstellung ist einfach unwiderstehlich: Wenn die Bestandteile zweier Objektmengen – jeder Gegenstand der einen Menge mit dem der anderen – in Überein-Stimmung gebracht werden können, dann enthält die eine Menge die gleiche Zahl von Gegenständen wie die andere. In der Mathematik spricht man bei einer solchen Eins-zu-eins-Entsprechung / wischen zwei Mengen häufig von einer Bijektion. Diese Verlagerung im Denken vom Abzählen zum Vergleichen von Mengen ist der Schlüssel zum Rätsel der Unendlichkeit.

Der Schlüssel zum Unendlichen
Zwei Mengen, deren Inhalte in eine Eins-zu-eins-Entsprechung umgesetzt werden können, haben die gleiche Größe. Schauen wir uns jetzt die Konsequenzen dieser harmlosen Aussage einmal an und sehen, wohin uns das Konzept der Eins-zu-eins-Entsprechung führt, bei kleinen Mengen wie dem Vergleich der Finger der linken Hand mit denen der rechten Hand oder der Sterne auf der amerikanischen Flagge mit den US -Bundesstaaten bedeutet die Eins-zu- eins-Entsprechung eindeutig Zahlengleichheit.

Jetzt sind wir bereit, einen Schritt ins Unbekannte zu wagen. Wir wollen Mengen betrachten, die unendlich viele Objekte haben. Wo könnten wir eine unendlich große Menge finden? Lassen wir die endlichen Beschränkungen der Wirklichkeit hinter uns und lassen wir unserer Phantasie freien Lauf.

Willkommen im Gasthaus zur Unendlichkeit. Wenn Sie das nächste Mal auf Reisen sind, dann vergessen Sie all die Hyatts, Hiltons, Ramadas, Vier Jahreszeiten und wie sie alle heißen. Sie müssen unbedingt eine Nacht im Gasthaus zur Unendlichkeit verbringen, im Hotel mit den zündenden Werbesprüchen Sie können auf so viele Zimmer zählen, wie es Zahlen zum Zählen gibt und Im (Jasthaus zur Unendlichkeit gibt es immer Platz. Das Gasthaus zur Unendlichkeit hat sich seinen Namen redlich verdient – seine Zimmer liegen alle nebeneinander und sind durchnummeriert von 1, 2, 3, 4 .. .bis unendlich. Auf jede abgezählte Zahl kommt ein Zimmer – was einen recht ansehnlichen Korridor ergibt. Lässt sich so ein Hotel in Wirklichkeit bauen?

Natürlich nicht. Aber in unserer Ideenwelt lässt es sich zweifellos errichten. Dieses Hotelsuitenszenario existiert nur in unserer Vorstellung, die wir so weit strapazieren, bis ein endloser Korridor enthalten ist, in dem sich Tür an Tür reiht, durch die man jeweils ein bescheidenes, aber reizvolles Hotelzimmer betreten kann Natürlich entspricht der erste Slogan der absoluten Wahrheit – für jede abgezählte Zahl gibt es ein Zimmer. Aber endet die Wahrheit in der Werbung des Gasthauses an dieser Stelle, oder ist der zweite Slogan ebenfalls wahr? Entspricht es der Wahrheit, dass solch ein riesiges Hotel das Schild Ausgebucht gar nicht benötigt? Natürlich lautet in unserer wirklichen Welt, in der es etwa 6,4 Milliarden Menschen gibt, die Antwort ja. Der Werbespruch ist wahr, wenn es endlich viele Menschen gibt, denn dann wird das Gasthaus zur Unendlichkeit stets ein Zimmer frei haben. Es gibt für jeden Menschen auf der Erde genügend Raum – selbst für die, die nicht mehr leben -, sodass jeder seine eigene Privatsphäre haben kann und immer noch unendlich viele Zimmer leer stehen. Diese unglaubliche Tatsache erlaubt es uns, einen besseren Eindruck von der Größe des Gasthauses zu bekommen – die ganze Menschheit könnte einchecken, und das Hotel wäre im Grunde immer noch leer!

Aber wenn wir uns die Vorstellung eines Hotels erlauben, das viel zu riesig ist, um in Wirklichkeit existieren zu können, warum sollten wir dann an dieser Stelle schon aufhören? Wir wollen daher unsere Vorstellungskraft noch ein wenig weiter strapazieren und uns ein Szenario ausdenken, das gleichermaßen unmöglich ist, nämlich eine Welt mit unendlich vielen Menschen. Gilt in dieser neuen fiktiven Welt wiederholt das Motto Im Gasthaus zur Unendlichkeit gibt es immer Platz? Wir wollen jetzt ein paar Szenarios untersuchen, die unsere Suiten füllen sollen, und werden sehen, ob wir es schaffen, unser Gasthaus zu überfüllen.

Ist Unendlichkeit plus eins grösser als die Unendlichkeit? Nehmen wir an, dass der Spielerkader der Saint Louis Cardinais sich so stark vergrößern würde, dass zum Team jetzt unendlich viele Spieler gehörten und jeder ein nummeriertes Trikot trüge: 1,2,3,4… unendlich. Als sie einmal wieder unterwegs sind, beschließen sie, ins Gasthaus zur Unendlichkeit einzuchecken, das völlig leer zu stehen scheint. Kann jeder Spieler ein Einzelzimmer bekommen? Selbstverständlich. Der Empfangschef gibt Spieler Nr. 1 das Zimmer Nr. 1, Spieler Nr. 2 das Zimmer Nr. 2 und so weiter.

Das heißt, jeder Spieler bekommt das Zimmer, dessen Nummer der Zahl auf seinem Trikot entspricht. Folglich haben wir eine Eins-zu-eins-Entsprechung zwischen den Spielern und den Zimmern hergestellt (Abbildung 11.3). Im Mannschaftsbus sitzen keine

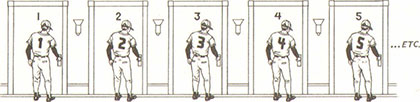
Abbildung 11.3: Eine offensichtliche Eins-zu-eins-Entsprechung zwischen Zimmern und Spielern

Spieler mehr, und alle Zimmer sind belegt. Deshalb sehen wir, dass die Anzahl der Spieler mit der Anzahl der Zimmer übereinstimmt, was nicht unbedingt eine Überraschung darstellt. Nun aber, da sämtliche der (unendlich vielen) Räume belegt sind, sieht es so aus, als müsse der Empfangschef tatsächlich das Schild Ausgebucht anknipsen. Er tut es und stößt einen Seufzer der Erleichterung aus, diese Arbeit erledigt zu haben.

In diesem Augenblick aber betritt der Eigentümer der Cardinais das Foyer und ist nicht gerade erfreut über das Ausgebucht- Schild. Der Empfangschef erklärt ihm, das Gasthaus sei komplett mit Spielern belegt, weshalb es keine freien Zimmer mehr gebe. Und was ist mit dem allerletzten Zimmer?, ruft der ruppige Clubboss. Der Angestellte verdreht die Augen und erklärt, es gebe kein letztes Zimmer, sondern nur eine endlose Zimmerflucht, die nun von einer ebenfalls endlosen Reihe von Spielern belegt worden sei. Als die Managerin des Gasthauses den Tumult am Empfangstresen mitbekommt, greift sie ein und steht vor einem frustrierten Empfangschef und einem verärgerten Clubbesitzer. Die Managerin beruhigt beide und versichert ihnen, sie werde den Besitzer schon so unterbringen, dass jeder Spieler weiterhin sein Einzelzimmer behalten kann. Sowohl der Angestellte als auch der Besitzer sind skeptisch, bis die Managerin ihren Neuanordnungsplan für die Zimmer ausführlich erklärt hat.

Und so funktioniert es: Sie wird jeden Spieler bitten, sein Zimmer zu verlassen und ins nächste Zimmer in numerischer Reihenfolge aufzurücken. Also wird Spieler Nummer i in Zimmer Nummer 2 ziehen, Spieler Nummer 2 in Zimmer Nummer 3, Spieler 3 in Zimmer 4 und so weiter (Abbildung 11.4). Wenn der Vorgang beendet ist, so viel ist offensichtlich, wird jeder Spieler weiterhin ein Einzelzimmer haben.

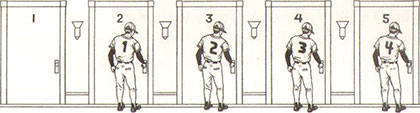
Abbildung 11.4: Jeder rückt auf ins nächstfolgende Zimmer und behält dadurch ein Einzelzimmer.

Selbst Spieler 14890003862 hat ein Zimmer – wissen Sie welches ? Natürlich Zimmer Nummer 14890003 863 .Jeder tut bereitwillig, worum er gebeten wurde, und zieht ins nächstfolgende Zimmer. Jetzt stellt die Managerin fest, dass Zimmer Nummer 1 frei ist, sodass der Besitzer der Cardinais einziehen und friedlich einschlafen kann.

Folglich sehen wir eine Eins-zu-eins-Entsprechung zwischen den Zimmern auf der einen Seite und den Spielern plus den Clubbesitzer auf der anderen Seite. Also hat durch die Hinzufügung eines neuen Mitglieds zur unendlichen Spielermenge deren Größe nicht zugenommen. Noch immer lässt sich eine Eins-zu-eins- Entsprechung zwischen Ensemble und Hotelzimmern herstellen. Sollte jetzt wieder eine Person auftauchen, wie beispielsweise der Trainer, könnten wir auf ähnliche Weise jeden (inklusive des Besitzers) bitten, ins nächste Zimmer aufzurücken. So behielte jeder ein Einzelzimmer, während für den Trainer Zimmer Nr. i frei würde. Selbst wenn noch 100 Leute einträfen, ließen sich alle Gäste um 100 Zimmer weiterrücken. Folglich nimmt die Größe einer unendlichen Menge durch Hinzufügung einer endlichen Zahl von Elementen nicht zu.

Ist die halbe Unendlichkeit kleiner als die Unendlichkeit? Nehmen wir jetzt an, dass im Laufe eines turbulenten Basketball-trainings das halbe Team verletzt wird. Es mag verrückt klingen, aber die verletzten Spieler sind genau die mit den ungeraden Trikotzahlen. Also werden die Spieler mit den Nummern 1, 3, 5, 7, 9, 11, 13 … und so weiter bis unendlich, begleitet vom Besitzer und vom Trainer, nach Hause geschickt. Nun aber ist das Hotel nur zur Hälfte belegt. Tatsächlich steht jedes zweite Zimmer leer. Mag diese Entwicklung auch jenen gefallen, die Frieden und Ruhe schätzen, so ist die Situation nicht unbedingt ideal zur Förderung des Teamgeistes. Also beschließen die Spieler, die im Gasthaus bleiben – das heißt, alle Spieler mit geraden Trikotnummern-, neue Zimmer zu beziehen, sodass sie alle nebeneinanderwohnen. Spieler 2 zieht in Zimmer 1; Spieler 4 zieht in Zimmer 2; Spieler 6 zieht in Zimmer 3, Spieler 8 zieht in Zimmer 4 und so weiter (Abbildung 11.5).

Sobald sie umziehen, bemerken wir etwa sehr Seltsames. Gibt es jetzt irgendwelche leeren Zimmer? Nun ja, in Zimmer 5 ist Spieler 10, in Zimmer 6 ist Spieler 12, Zimmer 22 ist von Spieler 44 belegt und Zimmer 23 ist das neue Zuhause von Spieler 46 und so weiter.

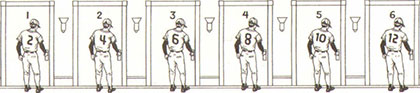
Abbildung 11.5: Eine Eins-zu-eins-Entsprechung zwischen den Zimmern und den Spielern mit den geraden Trikotnummern – jetzt sind alle Zimmer belegt.

Weiter hinten im Korridor sehen wir, dass Zimmer 1031021 ebenfalls besetzt ist – und zwar durch den Spieler mit der Nummer 2062042. Welches Zimmer wir uns auch anschauen oder uns auch nur vorstellen – überall wohnt jemand. Die Spieler mit den geraden Trikotnummern haben unwissentlich eine Eins-zu-eins-Entsprechung zwischen den Zimmern und sich selbst hergestellt, was uns aber mittlerweile wohlbekannt ist. Das heißt, nachdem die Hälfte der Elemente einer unendlichen Menge beseitigt worden ist, verändert sich die Größe der Menge nicht!

Der mathematische Term Kardinalität bezieht sich auf Größe, insbesondere wenn es um unendliche Mengen geht. Zwei Mengen haben die gleiche Kardinalität bedeutet, dass die Elemente der beiden Mengen in eine Eins-zu-eins-Entsprechung gesetzt werden können. Mathematisch ausgedrückt, haben wir also bewiesen, dass die Menge der geraden Zahlen die gleiche Kardinalität wie die Menge aller Zahlen hat. Im Grunde ist die halbe Unendlichkeit nicht kleiner als die Unendlichkeit.

Ist Unendlichkeit plus Unendlichkeit grösser als Unendlichkeit? Lassen Sie uns den Einsatz beträchtlich erhöhen. Nehmen wir an, das gesamte Team der Cardinais hält sich wieder im Gasthaus auf, da die Verletzten sich auskuriert haben. Spieler 1 ist in Zimmer 1, Spieler 2 in Zimmer 2 und so weiter. Statt lediglich ein oder zwei neue Leute einchecken zu lassen, wollen wir jetzt unendlich viele neue Leute hereinlassen und sehen, ob wir eine Überfüllung des Hotels erreichen können. Angenommen, ein neues Team taucht auf dem Schauplatz auf: die San Francisco Giants. Auch die Giants tragen die Zahlen 1, 2, 3,4 … unendlich auf ihren Trikots. Können wir die Aufrückmethode anwenden, um allen Giants ein Einzelzimmer zu bieten, ohne dabei die Cardinais auf die Straße zu setzen?

Wir können die Cardinais einmal umziehen lassen, um den ersten Giant in Zimmer i unterzubringen. Dann lassen wir die Cardinais ein zweites Mal umziehen, damit der zweite Giant in Zimmer 2 kommt. Tatsächlich können wir, wie wir bereits gesehen haben, beliebig oft endlich viele Umzüge veranlassen, um jede beliebige endliche Zahl von Giants hereinzulassen. Aber ließe sich das Aufrückverfahren auch unendlich oft durchführen, um alle Giants hereinzulassen? Nun, nehmen wir an, wir versuchten eine solche unendliche Verschiebung. Wie lautete dann die Zimmernummer des Cardinal-Spielers Nr. 1 ? Er kann ja nicht in Zimmer 1, 2, 3, 4 … oder in jedem anderen beliebigen Zimmer sein, denn jedes denkbare beliebige Zimmer wird eine endliche Anzahl von Zimmern von Zimmer 1 entfernt sein – und ein solches Zimmer ist von einem Spieler des Giant-Teams besetzt. Deshalb sitzt der Cardinal-Spieler Nr. 1 draußen auf der Bank und ist kein besonders glücklicher Spieler. Zumindest sitzt er zwischen seinen Teamkollegen, die auch vor die Tür gesetzt worden sind.

Es scheint daher, als wäre ein komplett ausgebuchtes Gasthaus zur Unendlichkeit überfüllt, wenn wir unendlich viel mehr Leute einchecken lassen. Oder nicht? Wir haben doch lediglich erkannt, dass die Methode des unendlichen Aufrückens nicht funktioniert. Aber vielleicht gibt es ja ein anderes Entsprechungsverfahren, das den Mitgliedern beider Teams die Zimmer in einer Eins- zu-eins-Methode zuordnet. Deshalb wollen wir versuchen, die Strategie abzuwandeln, die wir in der Situation mit den Spielern angewendet haben, deren Trikot eine gerade Zahl hatte.

Wir kehren also zu unserem ursprünglichen Szenario zurück, in dem Cardinal-Spieler 1 sich in Zimmer 1 befindet, Spieler 2 in Zimmer 2 und so weiter. Angenommen, wir bitten die Cardinais, dieses Mal anders umzuziehen. Spieler 1 soll in Zimmer 2 ziehen, Spieler 2 zieht in Zimmer 4, Spieler 3 zieht in Zimmer 6 und so weiter. Demnach zieht beispielsweise der Cardinal-Spieler 40211 in das Zimmer mit einer Zahl, die doppelt so groß ist wie die auf seinem Trikot, nämlich Zimmer Nr. 80422 (Abbildung 11.61). Folglich haben wir jeden Cardinal in einem neuen Zimmer untergebracht – das Team belegt jetzt alle Zimmer mit geraden Zahlen. Jetzt stehen aber alle Zimmer mit ungeraden Zahlen leer.

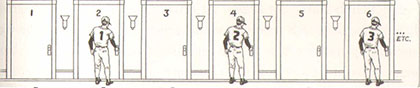
Abbildung 11.6: Das ganze Team ließe sich genau in den Zimmern mit den geraden Zahlen unterbringen.

Deshalb ließe sich jetzt der Giant-Spieler 1 in Zimmer 1 unterbringen, der Giant-Spieler 2 in Zimmer 3, Giant-Spieler 3 in Zimmer 5, Giant- Spieler 4 in Zimmer 7 und so weiter (Abbildung 11.7). Wir sehen also, dass jeder Giant ein Zimmer beziehen kann, ohne dafür einen Cardinal hinaus in die Kälte schicken zu müssen. Demnach haben wir eine Eins-zu-eins-Entsprechung zwischen den Zimmern und den Spielern beider Teams hergestellt.

Abbildung 11.7: Jeder Giant kann ein Einzelzimmer haben – das Team belegt alle Zimmer mit ungeraden Zahlen.

Folglich ergibt die Verdopplung der Unendlichkeit keine Menge, die größer ist als die ursprüngliche Unendlichkeit. Selbst wenn unendlich viele neue Gäste in einem bereits ausgebuchten Gasthaus eintreffen sollten, wird das Ausgebucht-Schild nicht benötigt. Vielleicht gibt es wirklich immer Platz im Gasthaus zur Unendlichkeit … oder doch nicht?

Eigentlich lautet die Frage: Ist jede Unendlichkeit gleich groß? Das heißt, lässt sich jede Unendlichkeit in eine Eins-zu-eins-Entsprechung mit der Menge der natürlichen Zahlen i, 2, 3 … bringen? Sowohl unsere Intuition als auch all die vorausgegangenen gescheiterten Versuche, das Gasthaus zu überfüllen, scheinen darauf hinzuweisen, dass Unendlichkeit Unendlichkeit ist. Aber in Wirklichkeit braucht unsere Intuition, wie wir bereits entdeckt haben, eine Umschulung, bevor wir unseren Verstand auf die Welt des Unendlichen loslassen können. Um zu veranschaulichen, wie unsere Intuition uns bei der Betrachtung des Unendlichen irreführen kann, verlassen wir jetzt das Gasthaus zur Unendlichkeit und paddeln durch eine wahre Flut von Tischtennisbällen.

Eine Reise in die Unendlichkeit – Lotto und Glücksspiele Tipps Teil 2