Eine Reise über die Unendlichkeit hinaus – Lotto und Glücksspiele Tipps Teil 1

Es gibt nichts Kleinstes unter dem Kleinen und nichts Größtes unter dem Großen; aber immer etwas noch Kleineres und noch Größeres.
Anaxagoros

Offensichtlich … Wir müssen nicht gleich unseren Steuerberater anrufen, wenn ein Kind uns mit unschuldiger Miene zu einem Kampf der Größten herausfordert. Wir sagen Zehn, und der Kleine antwortet voller Stolz: Elf. Nachdem wir angestachelt werden, es noch einmal zu versuchen, sagen wir: Eintausendsiebzehn!, während der kleine Engel, nicht im Mindesten verblüfft, mit Eintausendachtzehn! zurückschießt. Während wir noch versuchen, mit der Begeisterung unseres Nachwuchsnumerologen Schritt zu halten, stellen sich allmählich Kopfschmerzen ein, so- dass wir beschließen, diese Feierlichkeiten zu einem Ende zu bringen. Also sagen wir Unendlichkeit, was unser junger Gegner in ausgelassener Stimmung mit Unendlichkeit plus i! kontert. Mit diebischer Freude sagen wir Ha! und erklären, dass selbst mit der Hinzufügung von i die Unendlichkeit sich keinen Millimeter von ihrer ursprünglichen Größe fortbewegt. Selbst wenn wir zur Unendlichkeit die Unendlichkeit noch einmal hinzufügten, würde sie tatsächlich nicht an Größe zunehmen. Die Unendlichkeit, so sagt uns unsere Intuition, kommt nur in einer einzigen Größe vor: XXX … – L. Ende der Vorstellung.

Überraschung… Wäre das Kind altklug genug, würde das Spiel tatsächlich weitergehen – ja, eigentlich würde es unendlich lange weitergehen. Denn die Unendlichkeit tritt, genau wie die Zahlen, als stets in die Höhe wachsender Turm von Größen auf. Die Unendlichkeiten haben keine einheitliche Größe!

Die Suche nach etwas jenseits der Unendlichkeit
Man sollte denken, dass man alle anderen Unendlichkeiten kennt, sobald man eine gesehen hat, und dass die Suche nach etwas noch Größerem nicht nur sinnlos ist, sondern geradezu auf Gier schließen lässt. Als wir uns die Unendlichkeit als ein unbegreifliches Ganzes vorstellten, das alles enthält, machte es keinen Sinn, Dinge miteinander zu vergleichen, die unendlich waren – schließlich umfasste die Unendlichkeit schon alles. Als wir die Unendlichkeit verschwommen als das Nonplusultra in Größe betrachteten, schien es sinnlos, danach zu fragen, ob es etwas Größeres gäbe.

Nun aber entwickeln wir eine vertrautere – ja, wir wagen sogar zu sagen, intimere – Beziehung zur Unendlichkeit. Theoretisch schwebt uns eine weniger verschwommene Vision unendlicher Mengen vor. Wir haben mit unendlich vielen Tischtennisbällen jongliert, ohne dass uns das Herz stockte. Wir haben Hotels mit unendlich vielen Zimmern und ohne Angst wegen geklauten Shampoos bewältigt. Wir haben unendliche Mengen verglichen und uns die Mühe gemacht, darüber zu reden. Vielleicht können wir jetzt ja die scheinbar unmögliche Frage beantworten: Gibt es etwas, das größer ist als die Unendlichkeit, oder haben alle unendlichen Mengen die gleiche Größe?

Konzentration auf Eins-zu-eins-Entsprechungen
Die Frage, ob alle Unendlichkeiten gleich groß sind – oder, mathematisch umschrieben, ob sie alle die gleiche Kardinalität haben -, läuft im Prinzip auf folgende Frage hinaus: Ist es immer möglich, sie in eine Eins-zu-eins-Entsprechung zu bringen?

Bis jetzt sind unsere Begegnungen mit dem Unendlichen auf erfolgreiche Eins-zu-eins-Entsprechungen mit der Menge der natürlichen Zahlen hinausgelaufen. Jetzt aber wollen wir eine Menge beschreiben, die größer ist als die Menge der natürlichen Zahlen, das heißt, wir werden sehen, dass es unmöglich ist, die Elemente dieser neuen Menge in eine Eins-zu-eins-Entsprechung mit den natürlichen Zahlen zu bringen – jedes Mal werden zuerst die natürlichen Zahlen knapp. Deshalb ist diese neue Menge in Wirklichkeit größer als die Unendlichkeit aller natürlichen Zahlen!

Um diese neue Menge zu beschreiben, für die eine Eins-zu-eins- Entsprechung mit den natürlichen Zahlen nicht möglich ist, wollen wir nun ein kleines Spiel vorstellen, das einfach zu spielen und zu verstehen ist und dennoch enorme Auswirkungen hat – in der Tat: unendliche Auswirkungen.

Ausweichball
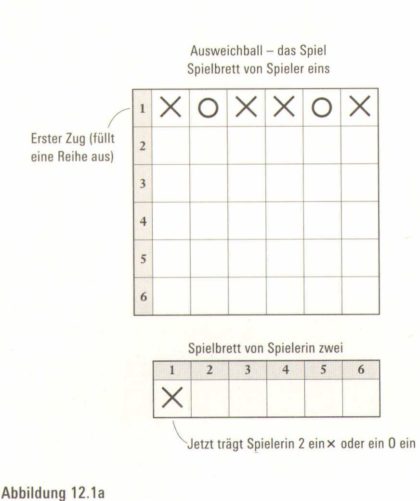
Ausweichball ist ein Brettspiel für zwei Spieler, die wir einfallslos Spieler eins und Spielerin zwei nennen wollen. Die beiden Spieler haben unterschiedliche Bretter (Abbildung 12.1), auf denen sie abwechselnd sechs aufregende Runden gegeneinander spielen.

Nach ein paar angemessenen Aufwärmübungen beginnt Spieler eins das Spiel, indem er entweder ein X oder ein O in jedes der sechs Kästchen in seiner ersten horizontalen Reihe einträgt. Dann denkt Spielerin zwei über die Situation nach und trägt in das erste Quadrat ihrer Reihe ein X oder ein O ein (Abbildung 12.1a).

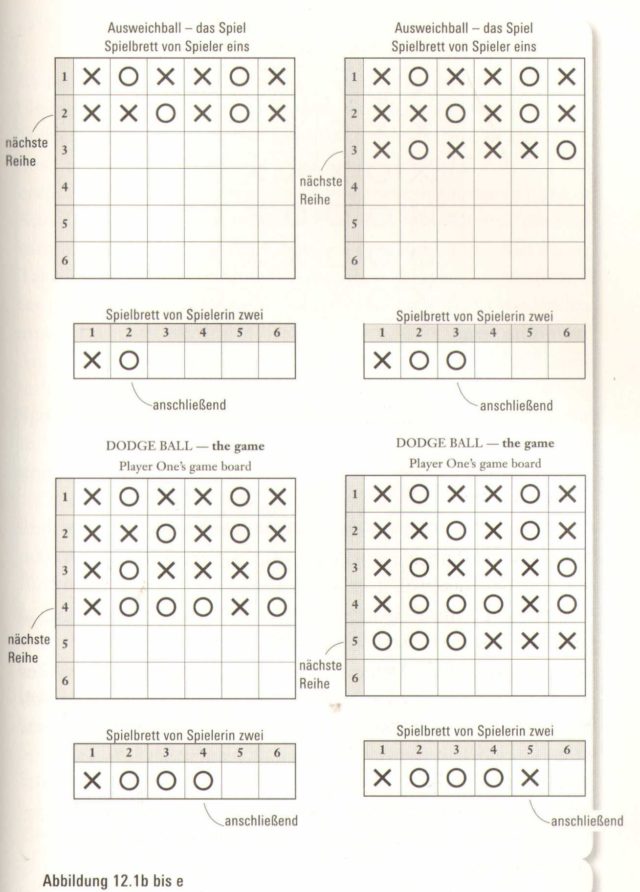
Spieler eins kratzt sich am Kopf und beginnt mit seiner zweiten Runde, in der es darum geht, die zweite Reihe mit einer beliebigen Reihenfolge von X und O auszufüllen. Spielerin zwei betrachtet sorgfältig die Züge von Spieler eins und antwortet mit einem x oder einem O im zweiten Kästchen ihres Bretts (Abbildung 12.1b). Spieler eins und Spielerin zwei fahren fort, abwechselns ihre Runden zu spielen, wobei Spieler eins stets eine ganze Reihe X und O schreibt und Spielerin zwei jeweils nur ein Kästchen ausfüllt (Abbildung i2.ic-e). Jeder spielt sechs Runden. Danach hat Spieler eins sechs Reihen mit X und O und Spielerin zwei eine Reihe mit X und O ausgefüllt (Abbildung 12.1)

Aber wer gewinnt? Spieler eins gewinnt, wenn irgendeine seiner sechs Reihen dieselbe Reihenfolge von X und O hat wie die einzelne Reihe X und O von Spielerin zwei. Das heißt, Spieler eins gewinnt, wenn eine seiner horizontalen Reihen mit der Reihe von Spielerin zwei übereinstimmt. Hier zählen nur horizontale Reihen. Von oben nach unten oder diagonal gelesene Reihen spielen in diesem Spiel keine Rolle. Spielerin zwei gewinnt, wenn ihre Reihe sich von jeder der sechs Reihen von Spieler eins unterscheidet, das heißt, sie gewinnt, wenn sie allen sechs Reihen von Spieler eins ausweichen konnte.

Manche Leute finden dieses Spiel langweilig, weil wir Bobby Fischer nicht konsultieren müssen, der uns die Raffinesse des Spiels erklärt.

Aber obwohl Ausweichball viel einfacher als Schach ist, geht das Spiel dennoch weit darüber hinaus, weil es uns zu unterschiedlichen Größen der Unendlichkeit führt.

Wie Spielerin zwei immer gewinnen kann
Es dauert nicht lange, bis man bemerkt, dass Spielerin zwei eine Gewinnstrategie hat: Sie tut einfach das Gegenteil von dem, was Spieler eins gerade getan hat. Das heißt, nachdem Spieler eins seine erste Reihe niedergeschrieben hat, schaut sich Spielerin zwei das erste Kästchen von Spieler eins an und trägt in ihr eigenes erstes Kästchen ein X ein, wenn Spieler eins ein O gewählt hat, oder sie nimmt ein O, wenn Spieler eins ein X genommen hat. Mit dieser Taktik sorgt sie garantiert dafür, dass ihre Reihe nicht mit der ersten Reihe von Spieler eins übereinstimmt – zumindest die beiden ersten Kästchen werden in beiden Reihen nicht übereinstimmen. Anschließend füllt Spieler eins eine zweite Reihe aus, und Spielerin zwei schaut sich das zweite Kästchen der zweiten Reihe von Spieler eins an. Erneut wählt sie das entgegengesetzte Zeichen für ihr zweites Kästchen. Spielerin zwei verfolgt diese Strategie weiter und gewinnt.

Dieses Spiel ist simpel und weit davon entfernt, aufregend zu sein, und leider wird die Firma Parkers Brothers, die Monopoly vermarktet, Ausweichball nicht in ihr Programm aufnehmen. Doch für unsere Zwecke ist die Einfachheit eine Tugend. Und das Spiel hat tatsächlich eine nennenswerte Eigenschaft. Die Gewinnstrategie von Spielerin zwei funktioniert nicht nur auf einem Brett mit 6X6 Feldern, sondern auf einem quadratischen Spielbrett jeder beliebigen Größe. Müsste sie ihre Strategie bei einem 8 X 8-Brett ändern (Abbildung 12.2)? Nein, die Strategie bleibt dieselbe, und Spielerin zwei gewinnt trotzdem. Doch was hat dieses alberne Spiel nun mit den verschiedenen unendlichen Größen zu tun?

Unendlicher Ausweichball
Nun sind wir bereit, mit einem Stabhochsprung aus dem Offen-sichtlichen hinüber ins Abstrakte zu wechseln und uns zu fragen, was es bedeutet, Ausweichball auf einem unendlichen Brett zu spielen. Das heißt, das Brett hat unendlich viele Reihen – Reihe i, Reihe 2, Reihe 3 … und so weiter bis unendlich, eine Reihe für jede natürliche Zahl, wobei jede Reihe unendlich viele Kästchen enthält (Abbildung 12.3).

Es ist aber vorstellbar, diese Ausweichballvariante unendlich lange zu spielen – Spieler eins macht eine unendliche Reihe X und O, worauf Spielerin zwei nur ein einziges Kästchen ausfüllt. Anschließend füllt Spieler eins die zweite unendlich lange Reihe aus, was Spielerin zwei mit einem zweiten Zeichen kontert… und so weiter bis ins Unendliche.

Wir wollen uns jetzt ansehen, was passierte, wenn Spielerin zwei die gleiche Strategie benutzte, die sie beim 6 X 6-Brett angewandt hat. Würden wir bis ans Ende all dieser unendlich vielen Züge warten, ist es nicht allzu schwierig, zu erkennen, dass Spielerin zwei eine unendlich lange Reihe erzeugt haben würde, die sich von jeder Reihe des Spielers eins unterschiede. Insbesondere wäre die Reihe von Spielerin zwei definitiv nicht die gleiche wie die erste Reihe von Spieler eins, weil der Eintrag ins erste Kästchen der Reihe von Spielerin zwei sich unbedingt vom Eintrag ins erste Kästchen der ersten Reihe von Spieler eins unterscheiden sollte. Ebenso wäre die Reihe von Spielerin zwei definitiv nicht die gleiche wie die zweite Reihe von Spieler eins, weil das zweite Kästchen in der Reihe von Spielerin zwei sich von dem zweiten Kästchen in der zweiten Reihe von Spieler eins unterscheidet. Wir sehen also, dass sich die Reihe von Spielerin zwei von jeder Reihe des Spielers eins unterscheidet. Also ist Spielerin zwei allen unendlich vielen Reihen von Spieler eins ausgewichen (Abbildung 12.4).

Natürlich könnte manch einer sagen, dieses Spiel werde niemals aufhören, weil die Spieler unendlich viele Spielzüge machen müssen. Aber angenommen, wir beschleunigten einfach das Spiel, wie es der Fall bei dem Tischtennisballrätsel war, und brächten es auf eine so unglaubliche Geschwindigkeit, dass alle unendlich vielen Einträge beider Spieler in 60 Sekunden geschafft wären. Demnach wäre das Spiel in einer Minute vorbei, und Spielerin zwei würde gewinnen und wohl erpicht darauf sein, ein neues Spiel zu wagen, und dieses Mal vielleicht um Geld spielen.

Dieses Spiel mag geradlinig und schlicht sein, und dennoch sind seine Auswirkungen verblüffend tiefgründig und der Intuition zuwiderlaufend. Vielleicht sollten wir über eine leichte Abänderung des Spiels nachdenken. Nehmen wir an, Spieler eins macht alle seine Züge, bevor Spielerin zwei irgendeinen Zug macht. Das heißt, Spieler eins setzt sich an sein Spielbrett und füllt es vollständig aus. Anschließend könnte Spielerin zwei sich alle Reihen anschauen und eine Reihe niederzuschreiben versuchen, die sich eindeutig von jeder Reihe unterschiedet, die Spieler eins hingeschrieben hat. Natürlich funktioniert die Gewinnstrategie von Spielerin zwei
prächtig, sich auf die diagonalen Einträge auf dem Spielbrett von Spieler eins zu konzentrieren – nämlich auf das erste Kästchen der ersten Reihe, auf das zweite Kästchen der zweiten Reihe und so weiter – und dann das Gegenteil davon hinzuschreiben, sodass sie, wie schon zuvor, gewinnt.

Dieses Spiel klingt Spieler eins gegenüber noch unfairer, da er das ganze Brett ausfüllen muss, bevor Spielerin zwei auch nur einen einzigen Eintrag in ihrer Reihe vorgenommen hat. An diesem Punkt erwägt Spieler eins, seinen Nachnamen in Zwei umzuwandeln.

Ein potenzieller Gewinnzug für Spieler eins
Versetzen wir uns in die bedauernswerte Situation von Spieler eins. Er versucht verzweifelt, seine Reihen so zu schreiben, dass eine davon genau der Reihe entspricht, die Spielerin zwei später hinschreiben wird.

Spieler eins könnte an die folgende faszinierende Strategie denken: Um sicherzugehen, dass Spielerin zwei eine Reihe von mir reproduziert, müsste ich einfach alle möglichen Reihen von X und O hinschreiben. Auf diese Weise muss Spielerin zwei, ganz gleich, was sie hinschreiben wird, auf jeden Fall eine meiner Reihen kopieren. Mit anderen Worten: Es ist, als kaufte man einen Lottoschein für jede mögliche Zahlenkombination und gäbe dabei viele Millionen Euro aus. Nur dann können wir sicher sein zu gewinnen, egal, welche Zahlen gezogen werden.

Oberflächlich betrachtet, sollte Spieler eins einmal über diese Strategie nachdenken. Schließlich hat Spieler eins unendlich viele Reihen zur Verfügung. Kann also Spieler eins diese Strategie anwenden und endlich einen Sieg verkünden?

Nehmen wir an, Spieler eins sei in der Lage, jeden denkbaren Verlauf von X und O – einen in Reihe i, einen in Reihe 2, einen in Reihe 3 und so weiter – hinzuschreiben. Ließen sich alle X- und O-Reihen tatsächlich so auflisten, dann geriete Spielerin zwei in Bedrängnis.

Warum die umfassende Strategie gar nicht so umfassend ist
Spielerin zwei ist nicht in Bedrängnis. Ganz gleich, was Spieler eins auch hinschreibt, Spielerin zwei hat immer eine Antwort. Spielerin zwei kann stets eine Reihe von X und O schreiben, die anders ist als jede Reihe, die Spieler eins hingeschrieben hat. Wir wissen, dass Spielerin zwei eine einfache Möglichkeit hat, all diesen Reihen auszuweichen. Sie schaut sich einfach das Brett von Spieler eins an, das mit lauter X und O ausgefüllt ist, geht dann die Diagonale entlang, wandelt jeden Eintrag ins Gegenteil um und schreibt so ihre Reihe hin. Daher beweist die Gewinnstrategie von Spielerin zwei in Wirklichkeit, dass es für Spieler eins unmöglich ist, seine umfassende Strategie erfolgreich anzuwenden. Mit anderen Worten: Das endlose Spielbrett ist nicht lang genug, um es Spieler eins zu ermöglichen, jede mögliche X- und O-Reihe aufzulisten. Was macht Spieler eins, wenn er ein unendliches Spielbrett vollständig ausfüllt? Spieler eins setzt jede Reihenzahl 1, 2, 3, 4, 5 … in Entsprechung zu einer unendlichen Liste von X und O. So, dass jede natürliche Zahl mit einem unendlichen X- und O-Verlauf verbunden ist.

Die Unendlichkeit gibt es in mehreren Größen
Die Gewinnstrategie von Spielerin zwei deutet darauf hin, dass es keine Möglichkeit gibt, eine Eins-zu-eins-Entsprechung zwischen den Reihennummern und allen denkbaren, unendlich langen X- und O-Reihen herzustellen. Anders ausgedrückt: Die Menge aller denkbaren X- und O-Reihen ist größer als die Menge der natürlichen Zahlen, aus denen die Reihennummern bestehen. Diese diagonale Strategie beweist, dass die Größe der Menge aller möglichen unendlichen X- und O-Verläufe größer ist als die Menge der natürlichen Zahlen (die Menge der Reihennummern).

Diese Erkenntnis ist so verblüffend, dass wir sie wieder in leicht abgewandelten Worten erklären wollen. Verblüffend ist diese Einsicht deshalb, weil wir schlüssig gezeigt haben, dass es mehr denkbare unendliche X- und O-Verläufe gibt, als natürliche Zahlen existieren. Wir erreichten dies, indem wir bewiesen, dass es unmöglich ist, eine Eins-zu-eins-Entsprechung zwischen den natürlichen Zahlen und der Menge aller möglichen unendlich langen X- und O-Reihen herzustellen – bei jedem diesbezüglichen Versuch können wir die Diagonale entlanggehen und einen X- und O-Verlauf erzeugen, der definitiv keiner einzigen anderen Zahl entspricht.

Folglich lassen sich nicht alle unendlichen Mengen in eine Eins- zu-eins-Beziehung zueinander setzen. Hier geht es insbesondere auch noch um zwei verschiedene Größen der Unendlichkeit, nämlich um die Größe der Menge der natürlichen Zahlen und um die Größe der Menge aller möglichen endlosen X- und O-Reihen. Die Unendlichkeit taucht nicht nur in einer einzigen Größe auf. Mathematisch formuliert, haben wir gezeigt, dass die Kardinalität der Menge der natürlichen Zahlen nicht die gleiche ist wie die Kardinalität der Menge aller möglichen X- und O-Reihen. Und unsere Reaktion darauf ist: Donnerwetter!

Zeit zum Durchatmen
Zuerst wollten wir hier einen leeren Raum lassen, weil wir hoffen, dass Sie das Gefühl haben, jetzt eine kleine Pause zu brauchen, um die Auswirkungen des unendlichen Ausweichballspiels erst einmal sacken zu lassen. Kein einzelner Schritt in dieser Logik ist schwierig, aber die Konsequenzen, die sich daraus ergeben, sind nicht gerade leicht verdaulich. Irgendwie fing alles mit einem albernen kleinen Spiel und einer simplen Strategie an, und ein paar Absätze später – puuh! – sind wir bereits an der Unendlichkeit vorbeigezischt.

Wir möchten Ihnen zusichern, dass die Logik dahinter unangreifbar und in Reichweite eines jeden Lesers ist, während das Ergebnis nicht so leicht akzeptierbar ist. Als Georg Cantor im späten 19. Jahrhundert als Erster bewies, dass die Unendlichkeit in mehreren Größen vorkommt, war die Mathematiker gemeinde zutiefst skeptisch, sodass Cantor im Mittelpunkt einer heftigen Kontroverse stand – Kriege unter Mathematikern sind keine Erfindung unserer Tage. Der Streit geriet so niederträchtig und persönlich, dass der arme Cantor schließlich in einem Irrenhaus landete. Inzwischen können wir glücklicherweise unterschiedliche unendliche Größen annehmen, ohne dass unser Verstand allzu sehr darunter leidet. Das Ergebnis aber ist so faszinierend, dass wir es zumindest aus ein paar unterschiedlichen Perspektiven betrachten sollten.

Um eine weitere Menge zu finden, die so ungeheuer unendlich ist, dass eine Eins-zu-eins-Entsprechung mit den natürlichen Zahlen nicht möglich ist, werfen wir alle Vorsicht über Bord und stopfen alle Laken in die Wäsche, während wir furchtlos darangehen, unser Gasthaus zur Unendlichkeit sauber zu machen.

Die Kardinalitätsreinigung
Wir kehren jetzt zum Gasthaus zur Unendlichkeit zurück und stoßen dort auf eine von vielen Herausforderungen in der Welt der unendlichen Gästebetreuung. Erinnern Sie sich, dass unser unendliches Hotel Zimmer mit den Nummern i, 2, 3, 4, 5 … hat. Jetzt fällt bei all diesen vielen Zimmern natürlich eine Menge Reinigungsarbeit an. Deshalb hat dieses Hotel einen Vertrag mit der Kardinalitätsreinigung, die sich darauf spezialisiert hat, Verschmutzungen größten Ausmaßes zu bewältigen. Aber selbstverständlich ist das Hotel nicht jede Nacht ausgebucht, sodass die Hotelmanagerin jeden Morgen die Kardinalitätsreinigung anruft und dem Manager mitteilt, welche Zimmer sauber gemacht werden müssen. An einem Morgen müssen vielleicht nur die Zimmer mit geraden Nummern gereinigt werden, an einem anderen Morgen muss der Service sich womöglich nur um die Zimmer 1, 2, 3, 17 und 307 kümmern.

Wie Sie sich denken können, erfordert die Reinigung eines Gasthauses zur Unendlichkeit hochspezialisiertes und geschultes Personal, das der Kardinalitätsreinigung zur Verfügung steht. Tatsächlich ist jeder der Angestellten nur auf eine bestimmte Menge von Räumen spezialisiert. So wird beispielsweise ein Angestellter gerufen, wenn die Zimmer mit den geraden Nummern gereinigt werden müssen. Ein anderer Kollege erledigt die Arbeit, wenn alle Zimmer mit geraden Nummern, außer Zimmer 2 und 12, dran sind. Wieder ein anderer Mitarbeiter wird geschickt, wenn lediglich die Zimmer 2, 4, 8, 16, 32, 64 … es nötig haben. Auch für die Anzahl der Räume 1,2,6,1007 und 20149 – und ausschließlich für diese – ist ein anderer Kollege zuständig. Den schlimmsten Job hat jener arme Willi erwischt, der gerufen wird, jedes Zimmer gereinigt werden muss. Und den bequemsten Job hat jener glückliche Spezialist, der alarmiert wird, wenn kein Zimmer sauber gemacht werden muss – prima Arbeit, wenn man sie ergattern kann.

Mit anderen Worten: Angesichts jeder beliebigen Liste verschmutzter Zimmer gibt es bei der Kardinalitätsreinigung genau einen Mitarbeiter, der beauftragt wird, genau diese Zimmer zu säubern – keines mehr und keines weniger. Also arbeitet an jedem beliebigen Tag jeweils nur eine Person, während für jede mögliche Anordnung schmutziger Zimmer ein anderer Angestellter der Kardinalitätsreinigung in Frage kommt – eine wirklich seltsame Geschäftsidee. Man könnte glauben, das Hotel wäre besser dran, wenn es jedem Zimmer eine Person zuteilte, die ausschließlich dieses Zimmer reinigte. Aber ob diese Maßnahme nun besser wäre oder nicht, soll für unser fiktives Szenario keine Rolle spielen. Wir sollten diesen albernen Geschäftsplan der Kardinalitätsreinigung einfach akzeptieren – nur ein einziger Mitarbeiter ist täglich für die Reinigung zuständig.

Trotz einiger erstaunlicher Ungerechtigkeiten, was die Arbeitslast betrifft (der Kollege, der nur die Zimmer 23, 48, 102 und 100034567 sauber macht, neigt dazu, dem Kollegen, dessen Job es ist, alle Zimmer mit ungeraden Nummern zu säubern, aus dem Weg zu gehen), herrscht beim Team der Kardinalitätsreinigung ein ausgezeichnetes Betriebsklima. Die gute Stimmung zwischen Management und Personal könnte nicht besser zur Geltung kommen als während der Feiertage im Dezember. Als Gratifikation zum Jahresende buchen die Besitzer der Kardinalitätsreinigung jedes Zimmer im Gasthaus zur Unendlichkeit, sodass die Angestellten dort ein Wochenende verbringen können. Bei diesem großzügigen Angebot gerät die Gastfreundschaft des Hauses an ihre Grenzen – jeder Angestellte muss ein Einzelzimmer bekommen. Sie kommen alle in großartiger Urlaubsstimmung an – es wirFeiertagsjubeld Eierlikör serviert, bevor man ins Hotel eincheckt – und bitten den Empfangschef, ihnen die Zimmer zuzuweisen.

Einer bekommt Zimmer Nummer 1, ein anderer wird in Zimmer 2 untergebracht, wieder ein anderer in Zimmer 3 und so weiter. Bedenken Sie, dass es keine Bettgenossen gibt – jeder spezialisierten Reinigungskraft war ein Einzelzimmer zugesagt worden (was alle zweifellos auch verdient haben). Also versucht der Empfangschef, für jeden Mitarbeiter ein Zimmer zu finden, doch bei jeder Zuweisung, die er sich überlegt, scheint das Hotel voll zu sein, bevor alle ihre Einzelzimmer haben. Als Empfangschef eines Gasthauses mit unendlich vielen Zimmern kann er normalerweise jeden Gast unterbringen. Heute aber kommt er einfach nicht voran. Wie er den Raumpflegern die Zimmer auch zuteilt – jedes Mal scheinen ein paar Mitarbeiter dabei leer auszugehen. Wie kann das geschehen? Wir sollten einen Gang zurückschalten und ein wenig mehr über unsere Raumpfleger in Erfahrung bringen.

Ausweichball mit den Raumpflegern spielen
Natürlich hat jeder Raumpfleger einen Namen, und das Management der Kardinalitätsreinigung kennt sie alle. In der modernen Geschäftswelt wäre es allerdings typischer, wenn jeder Angestellte einen Identifikationscode hätte. Eine Codierungsmöglichkeit bestünde darin, jede Person nach der Ansammlung von Zimmern zu benennen, die sie reinigt. Dies ließe sich verwirklichen, indem man jedem Mitarbeiter einen endlosen Verlauf von X und O zuwiese. Jeder Buchstabe stünde dann für ein Hotelzimmer in numerischer Reihenfolge – der erste Buchstabe steht für Zimmer i, der zweite Buchstabe für Zimmer 2 und so weiter. Der Buchstabe ist ein X, wenn der Raumpfleger dieses Zimmer reinigt, und ein O, wenn er dieses Zimmer nicht betreut. Also ist beispielsweise Raumpfleger OxOxOxOxOxOxOxOxOxOx… die Person, die alle Zimmer mit geraden Nummern reinigt (beachten Sie, dass das X für die Zimmer mit den geraden Nummern stehen), während Raumpfleger XXOXXOXOOOOOOOO … der Mitarbeiter ist, der nur die Zimmer 1,2,4 und 7 reinigt.

Nehmen wir an, wir hätten alle Zimmer im Gasthaus zur Unendlichkeit mit Raumpflegern belegt. Wer befindet sich wo? Wir tragen jetzt alle Zimmernummern senkrecht in eine Liste ein und schreiben neben jede Zimmernummer die Reihe von X und O, die den Raumpfleger identifiziert, der dieses Zimmer bezogen hat. Wenn wir jetzt die Diagonalstrategie anwenden, die Spielerin zwei benutzte, um beim unendlichen Ausweichballspiel zu gewinnen, können wir einen Raumpfleger benennen, der sich in keinem Zimmer aufhält. Wir könnten einfach die X und O entlang der Diagonalen in ihr Gegenteil verkehren, wie wir es beim Ausweichballspiel getan haben, und so den Namen eines anderen Raumpflegers ermitteln – eines Mitarbeiters, der sich von denen unterscheidet, die ein Zimmer haben. Genau dieser Kollege sitzt auf der Straße.

Man könnte diesen armen Wicht einen Straßenfeger nennen (Abbildung 12.5).
Die Gewinnstrategie für das Ausweichballspiel zeigt, dass wir, ungeachtet der Versuche des Empfangschefs, die Räume zu vergeben, stets einen Raumpfleger ohne Zimmer benennen können. Folglich ist eine Eins-zu-eins-Entsprechung zwischen den beiden Mengen unmöglich, sodass wir zu dem Schluss gelangen, dass die Menge aller Beschäftigten bei der Kardinalitätsreinigung in Wirklichkeit größer ist als die Menge der natürlichen Zahlen (Zimmernummern). Jeder denkbare Versuch des Empfangschefs, den Raumpflegern Zimmer zuzuweisen, ist zum Scheitern verurteilt. Auf jede mögliche Zuweisung kommt mindestens ein Mitarbeiter, der draußen in der Kälte stehen bleibt. Folglich gelangen wir zu dem unausweichlichen Fazit, dass es mehr Angestellte bei der Kardinalitätsreinigung gibt als Zimmer im Gasthaus zur Unendlichkeit.

Etwas offizieller formuliert: Es gibt keine Eins-zu-eins-Entsprechung zwischen der Menge aller natürlichen Zahlen (die Zimmernummern) und der Menge aller möglichen Mengen natürlicher Zahlen (also alle möglichen Mengen von Zimmern, die an irgendeinem bestimmten Morgen gereinigt werden müssen).

Eine Reise über die Unendlichkeit hinaus – Lotto und Glücksspiele Tipps Teil 2