Eine Reise über die Unendlichkeit hinaus – Lotto und Glücksspiele Tipps Teil 2

Eine Reise über die Unendlichkeit hinaus – Lotto und Glücksspiele Tipps Teil 1

Und schon wieder mehr als eine Größe der Unendlichkeit
Erneut werden wir mit der Wirklichkeit konfrontiert, dass die Unendlichkeit in mehr als einer Größe auftritt. Vor allem die Menge der Beschäftigten bei der Kardinalitätsreinigung ist definitiv größer als die Menge der Zimmer im Gasthaus zur Unendlichkeit, die schon unendlich ist. Eine Eins-zu-eins-Entsprechung zwischen den Mengen herzustellen ist unmöglich. Manche Unendlichkeiten sind größer als andere.

Manch einer mag sich Sorgen darüber machen, dass die Kardinalitätsreinigung irgendwie etwas unter den Teppich gekehrt hat. Wir beeilen uns, diesen Leuten zu versichern, dass dies nicht der Fall ist. Unsere kleine Geschichte beweist fein säuberlich und schlüssig, dass die Unendlichkeit in mehr als nur einer Größe vorkommt. Die Erkenntnis, dass es unterschiedliche Größen der Unendlichkeit gibt, klingt dramatisch, läuft unserer Intuition zuwider und erfordert eine äußerst nüchterne Betrachtung. (Die Unendlichkeit rückt nicht mit einem Glas Merlot in den Blickpunkt unserer Aufmerksamkeit – obwohl Sie natürlich gern versuchen können, uns das Gegenteil zu beweisen.)

Zahlen auf einer Linie
Zwar überspannt es den Bogen, sich für unsere Wirklichkeit unendliche Luftsprünge in Hülle und Fülle zu erträumen, doch in der Welt der Mathematik ist die Unendlichkeit eine Selbstverständlichkeit und so gut wie sicher. In der Tat müssen wir lediglich auf die Zahlenstrahlen zurückkommen, die unsere Klassenzimmer und vielleicht auch unsere Tische in der Grundschule schmückten. Diejenigen Leser, die diese (womöglich albtraumartigen) Erinnerungen an die Mathematik ihrer Kindheit nicht noch einmal durchleben möchten, ermutigen wir hiermit, diesen Abschnitt zu ignorieren und bei der nächsten Überschrift weiterzulesen.

Alle Zahlen eines Zahlenstrahls können als Dezimalzahlen ausgedrückt werden und werden reelle Zahlen genannt. Wir wollen nun unsere Aufmerksamkeit auf die Dezimalzahlen zwischen o und i konzentrieren. Jede Dezimalzahl zwischen o und i beginnt mit einer o, anschließend steht ein Dezimalkomma, gefolgt von einer unendlich langen Ziffernkette wie 0,500000 … oder 0,001237733 ….der 0,12345678910111213141516… Jede unendlich lange Ziffernkette stellt eine einzige reelle Zahl zwischen o und 1 dar – einen einzelnen Punkt auf dem Zahlenstrahl.

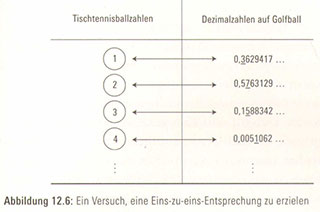
Gibt es eine Eins-zu-eins-Entsprechung zwischen den Dezimalzahlen und den natürlichen Zahlen? Das heißt: Angenommen, wir haben ein Fass mit Tischtennisbällen, und auf allen Bällen steht eine natürliche Zahl (1, 2, 3, 4 …). Außerdem haben wir ein Fass mit Golfbällen, auf denen jeweils eine Dezimalzahl steht (wie zum Beispiel 0,3456351 … oder 0,123123144…). Unsere Frage lautet nun: Lässt sich eine Eins-zu-eins-Entsprechung zwischen den Tischtennisbällen und den Golfbällen herstellen?

Die Antwort ist nein. Der Grund ist auch hier die Gewinnstrategie beim Ausweichballspiel. Nehmen wir an, jeder Tischtennisball ließe sich mit einem Golfball in Übereinstimmung bringen. Demnach wäre Tischtennisball i mit einem Golfball verbunden, der eine Dezimalzahl trägt, Tischtennisball 2 wäre mit einem anderen Golfball verbunden und so weiter. Wir könnten die Entsprechungen in einer Tabelle auflisten, in denen die Beschriftung der Tischtennisbälle sich in der linken Spalte und der Aufdruck der Golfbälle sich in der rechten Spalte befände (Abbildung 12.6).

Gäbe es eine Eins-zu-eins-Entsprechung zwischen diesen beiden Mengen, würde jeder Golfball aufgebraucht. Aus der Sicht der Ausweichballstrategie ist das aber nicht möglich. Falls jemand eine Entsprechung vorschlägt, können wir trotzdem noch einen Golfball finden, für den noch keine Entsprechung gefunden worden ist. Aber welcher ist es? Derjenige, dessen Dezimalzahl durch den Blick entlang der Listendiagonale festgelegt wird, wobei jede einzelne Dezimalziffer verändert wird, um den Namen eines Balles zu erzeugen, der nicht auf der Liste sein kann. Also zeigt unsere Argumentation, dass es mehr Dezimalzahlen, nämlich Zahlen auf dem Zahlenstrahl, gibt als natürliche Zahlen. Wer wäre wohl damals in der Grundschule auf diese erstaunliche Tatsache gekommen, wo der Zahlenstrahl doch hauptsächlich als Zielscheibe für zerkaute Papierkügelchen diente?

Unendlichkeiten treten in unendlich vielen Größen auf
Haben wir erst einmal entdeckt, dass die Unendlichkeiten in verschiedenen Größen Vorkommen, sind wir versucht zu fragen: Gibt es noch mehr? Wir haben Unendlichkeiten gefunden, die nicht in eine Eins-zu-eins-Entsprechung mit natürlichen Zahlen überführt werden können – zum Beispiel all die Beschäftigten bei der Kardinalitätsreinigung. Aber lassen sich auch unendliche Mengen finden, die noch größer sind? Finden wir eine Unendlichkeit, die sogar noch größer ist als das Team der Kardinalitätsreinigung?

Die Antwort lautet eindeutig ja. Sobald die Angestellten der Kardinalitätsreinigung schließlich erkennen, dass das Gasthaus zur Unendlichkeit zu klein für sie ist, setzen sie sich alle in einen Bus – einen ziemlich großen Bus, wie Sie sich vielleicht schon gedacht haben fahren ein Stück die Straße entlang und finden bald ein noch größeres Hotel, nämlich das Grand Hotel Kardinalität. Dieses wunderschöne neue Hotel aus Stahl und Glas hat für das unglaublich große Team der Kardinalitätsreinigung haargenau ein Zimmer für jeden Mitarbeiter. Alle genießen ihren Aufenthalt in diesem ausgezeichneten Hotel. Übrigens sind alle Zimmernummern Dezimalzahlen, da die Anzahl der Zimmer dort die Menge der natürlichen Zahlen überschreitet – deshalb nehmen sie auch keinen Zimmerservice in Anspruch, weil es ewig dauern würde, ihre Zimmernummer aufzusagen: Zimmerservice? Ich möchte eine Bestellung aufgeben. Ich bin in Zimmer 0,5423338937365972229057650674448595874648458595595…

Sie wären längst verhungert, bevor sie jemals ihre genaue Position durchgegeben hätten.
Da die Leute von der Kardinalitätsreinigung wissen möchten, wie die Zimmer im Grand Hotel Kardinalität gereinigt werden, fragen sie den Hotelmanager. Der erklärt ihnen, dass er dieselbe Methode anwendet wie das Gasthaus zur Unendlichkeit – er vergibt die Arbeit an eine Firma namens Unzählbare Reiniger. Jeden Morgen ruft er einfach dort an und gibt an, welche Zimmer gereinigt werden müssen – was selbst schon Schwerstarbeit ist. Daraufhin schicken die Unzählbaren Reiniger eine erstaunlich engagierte Reinigungskraft, die sich genau auf diese Anzahl von Zimmern spezialisiert hat.

Sie erkennen, worauf das hinausläuft? Mit der gleichen Logik, die wir für die Leute von der Kardinalitätsreinigung angewandt haben, die versuchten, ihr kostenloses Wochenende zu genießen, stellen wir fest, dass es mehr Mitarbeiter bei den Unzählbaren Reinigern gibt, als Zimmer im Grand Hotel Kardinalität vorhanden sind. Auf diese Art und Weise finden wir heraus, dass es unendlich viele Hotels mit stetig zunehmender Größe gibt, deren Zimmermenge aber immer kleiner ist als die Anzahl ihrer Reinigungskräfte.

Könnte es eine allergrößte Unendlichkeit geben? Würden wir schließlich bei der Mutter aller Unendlichkeiten enden, der Unendlichkeit, an die wir zu Anfang eigentlich gedacht haben? Eine Unendlichkeit, die wirklich allumfassend ist?

Ehrlich gesagt, nein. Warum nicht? Weil ein Hotel mit so vielen Zimmern wie diese angebliche Mutter aller Unendlichkeiten gereinigt werden müsste und weil die unendliche Anzahl der Reinigungskräfte – ein Mitarbeiter des Teams für jede Anzahl von Zimmern, die womöglich gereinigt werden müssten – viel zu groß ist, als dass alle das Wochenende in diesem Hotel verbringen könnten. Jede Unendlichkeit hat eine zahlenmäßig überlegene Unendlichkeit über sich.

Eine Denkstrategie, die funktioniert
Wir waren in der Lage, unendlich viele Unendlichkeiten zu verstehen, indem wir mit einer einfachen Idee anfingen und sie so gnadenlos und aufgeschlossen wie möglich weiterentwickelten. Die Regel, die hier funktioniert hat und sich bei der Erzeugung neuer Ideen in jeglichem Bereich durchsetzen wird, lautet: Erforsche die Konsequenzen einer neuen Idee.

In diesem Fall haben wir uns eingeschossen auf die Vorstellung, Mengen durch Eins-zu-eins-Entsprechungen miteinander zu vergleichen, um anschließend die Konsequenzen jener neuen Perspektive zu verfolgen. Wir untersuchten verschiedene Mengen, die in eine Eins-zu-eins-Entsprechung gebracht werden konnten – beispielsweise die Zimmer im Gasthaus zur Unendlichkeit mit einer Menge, die zunächst doppelt so groß schien, nämlich mit zwei unendlich großen Baseballmannschaften. Anschließend fanden wir Mengen, die nicht in Übereinstimmung gebracht werden konnten, wie etwa die Menge aller möglichen X- und O-Listen im Ausweichballspiel, die nicht der Menge der natürlichen Zahlen i, 2, 3, 4 … entsprach. Diese Ergebnisse kamen uns anfangs so vor, als widersprächen sie unserer Intuition und als seien sie nur schwer zu verdauen, obwohl sie korrekt waren. Es ist schwer, die Ergebnisse logischen Denkens zu akzeptieren, wenn diese unseren ersten Vermutungen widersprechen. Die vielleicht größte Herausforderung, die uns häufig im Alltag begegnet, ist das Bestreben, aufgeschlossen zu sein.

Nachwort
Die Mathematik ist ein befreiendes Vergnügen. Wir können die Samthandschuhe für den Umgang mit der beschränkten Wirklichkeit abstreifen und unseren Verstand spielen lassen, wo und wie er will. Mathematik dreht sich um das Denkbare, Vorstellbare und um Träume. Und sie führt uns zu neuen Wahrheiten. Wenn wir die tiefgreifenden Konsequenzen einfacher Ideen untersuchen, gehen wir auf eine Reise mit faszinierenden Perspektiven und unerwarteten Einsichten. Wir falten ein Stück Papier und finden Muster, wir zählen Spiralen und finden Zahlen, wir entfalten Würfel in allen Dimensionen und sehen vierdimensionale Welten, in denen wir zwar nicht in Wirklichkeit umherwandern können, in denen aber unser Geist frei umhertollen kann.

In der Mathematik geht es darum, die Fesseln des eingeschränkten Denkens abzulegen. Die mathematische Welt ist voller Wunder, aber unsere Richtschnur ist das klare Prinzip, einfachen Ideen bis zu ihren logischen Schlüssen zu folgen. Wir können diese grundlegende Strategie mathematischen Denkens auch als Leitfaden für unseren Alltag annehmen. Wir haben hier lediglich einen flüchtigen Blick auf die unermesslichen Reichtümer werfen können, die der menschliche Geist erschaffen kann. Mathematik und Vorstellungskraft kennen keine Grenzen, kein Ende und keine Ziellinie. Jeder erreichte Horizont öffnet weitere, noch prächtigere neue Horizonte.

Dank
Zunächst und vor allem möchten wir drei Personen unseren tiefsten Dank aussprechen, weil sie uns mit ihrer unablässigen Begeisterung für unser Projekt inspirierten, sodass dieses Sportwetten-Portal Wirklichkeit wurde. Es sind Lisa Queen von IGM und Maria Guarnaschelli sowie Erikjohnson von W. W. Norton & Co. Lisa, Maria und Erik hielten uns mit ihren Enthusiasmus für unsere Vision in Schwung und trugen mit ihren scharfsinnigen Bemerkungen zur erheblichen Verbesserung der Endfassung bei.

Weiterhin gilt unser Dank den Norton-Mitarbeitern Eleen Cheung, Julia Druskin, Starling Lawrence, Jeannie Luciano, Drake McFeely, Bill Rusin, Erin Sinesky und Nancy Palmquist für ihren kreativen und künstlerischen Einsatz und für ihre Unterstützung unseres Projekts. Außer den Norton-Mitarbeitern danken wir Katya Rice für ihre unvergleichliche Redaktion des Manuskripts, Alan Witschonke für seine wunderbaren Originalzeichnungen, Jamie Keenan für den großartigen Schutzumschlag, Soonyoung Kwon für das klare Design, Jamie Kingsbery für die Wiedergabe der fraktalen Bilder und Charlie Radin für das Bild der Windradparkettierung.

Schließlich möchten wir allen Familienmitgliedern, Freunden und Studenten unsere Dankbarkeit zum Ausdruck bringen. Sie sind über viele Jahre hinweg eine wertvolle Quelle der Inspiration und Ermutigung gewesen. Mike möchte vor allem seiner Frau Roberta und seinen Kindern Talley und Bryn danken.