Eine Reise in die Unendlichkeit – Lotto und Glücksspiele Tipps Teil 2

Eine Reise in die Unendlichkeit – Lotto und Glücksspiele Tipps Teil 1

Ein Tischtennisrätsel – mit spektakulärer Geschwindigkeit geworfene Bälle
Wir wollen uns nun unendlich viele Tischtennisbälle vorstellen, die wie kleine kugelige Soldaten in Reih und Glied stehen. Auf jedem Ball steht eine Zahl – 1, 2, 3, 4, 5 … und so weiter bis unendlich-, wobei alle Bälle in numerischer Reihenfolge angeordnet sind. Unser Verstand hat keinerlei Probleme, sich einen solch unmöglichen Anblick vorzustellen. Neben diesem Heer nummerierter Tischtennisbälle sehen wir ein riesiges Holzfass, das größer ist als jedes Fass, das wir je gesehen haben oder je sehen werden. Nun sind wir bereit für ein Hochgeschwindigkeitsabenteuer von
60 Sekunden Dauer, das so nur im Reich unserer Vorstellungskraft stattfinden kann (Abbildung 11.8).

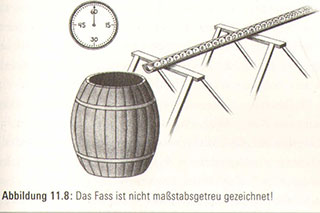
Wir drücken auf die Stoppuhr, die einen roten Sekundenzeiger hat, der bei o zu laufen beginnt und für eine Umdrehung 60 Sekunden braucht. Wir fangen gemächlich an: In der ersten halben Minute (30 Sekunden) lassen wir die Bälle 1 bis 10 in das Fass fallen, greifen dann ins Fass hinein, nehmen den Ball Nr. 1 heraus und werfen ihn weg. Diese Aufgabe lässt sich leicht in 30 Sekunden bewältigen. Nun bleiben uns noch 30 Sekunden, sodass wir den Ablauf etwas beschleunigen. In der Hälfte der verbleibenden Zeit (15 Sekunden) lassen wir die nächsten zehn Bälle mit den Nummern 11 bis 20 ins Fass fallen, greifen wieder hinein und werfen den Ball mit der Nummer 2 hinaus. Sollten Sie glauben, das sei schnell gegangen, dann schauen Sie jetzt genau zu. In der Hälfte der verbleibenden Zeit (7,5 Sekunden) fügen wir die nächsten zehn Bälle in der Reihe – von 21 bis 30 – hinzu, greifen ins Fass, fischen Ball Nr. 3 heraus und werfen ihn weg. Auf diese Weise fahren wir fort – in der Hälfte der verbleibenden Zeit lassen wir die nächsten zehn nummerierten Tischtennisbälle in das Fass fallen und suchen und werfen den Ball mit der niedrigsten Zahl heraus.

Schauen wir uns an, wie dies wirklich funktioniert. In der ersten Halbzeit (das heißt, in den ersten 30 Sekunden, der Hälfte der 60 Sekunden) werfen wir die Bälle 1-10 ins Fass und entfernen Ball 1. In der zweiten Halbzeit (15 Sekunden, die Hälfte der verbleibenden Zeit) fügen wir Ball 11- 20 hinzu und entfernen schnell Ball 2. In der dritten Halbzeit (7,5 Sekunden) werfen wir die Bälle 21-30 hinein und entfernen Ball 3. Während der vierten Halbzeit (bloße 3 ZA Sekunden) werfen wir die Bälle 31-40 ins Fass und entfernen Ball 4. Dieses Verfahren wird fortgesetzt, bis die Stoppuhr die 60-Sekun- den-Marke erreicht. Dann ist das Experiment vorbei.

Beachten Sie: Während wir dem Ende näher kommen, nimmt unsere Geschwindigkeit stetig zu – wir werden bemerkenswert schnell. Eigentlich müssten wir in kürzester Zeit schneller als der Schall arbeiten – dann wären wir nicht einmal mehr in der Lage, uns beim Denken zuzuhören. Und bald nachdem wir die Lichtgeschwindigkeit hinter uns gelassen haben, würden wir vermutlich einfach verschwinden. Tatsächlich würden wir bald wesentlich schneller als mit Lichtgeschwindigkeit arbeiten. Was ja wohl unmöglich wäre. Richtig – aber das trifft auch auf den Anblick von unendlich vielen nummerierten Tischtennisbällen zu. Lassen wir also die physikalischen Beschänkungen unserer Wirklichkeit hinter uns und stellen wir uns vor, dieses Experiment allein im Kopf durchzuführen.

Wir wollen diese Runden deshalb mit zunehmender Geschwindigkeit absolvieren, um uns in die Lage zu versetzen, uns unendlich viele Runden 10 rein, 1 raus vorzustellen und uns dann die Ergebnisse anzuschauen. (Alternativ könnten wir eine Runde pro Minute spielen und uns dann fragen, was nach dem Verstreichen eines unendlichen Zeitraums geschehen ist. Beide Methoden funktionieren.)

Auf jeden Fall sind nach unendlich vielen Runden das Experiment und die 60 Sekunden vorbei. Und wir sind müde – schneller als mit Lichtgeschwindigkeit zu arbeiten kann auch dem Tatkräftigsten den Wind aus den Segeln nehmen. Sobald wir uns beruhigt und unsere Fassung wiedergewonnen haben, gehen wir zum Fass und schauen hinein. Was sehen wir? Ist das Fass nun gefüllt mit unendlich vielen Tischtennisbällen, enthält es eine endliche Menge Tischtennisbälle, oder ist es leer? Was glauben Sie? Äußern Sie eine Vermutung. Trauen Sie sich.

Eine vernüftige Vermutung. Eine Möglichkeit, das Problem anzugehen, besteht darin, sich zu überlegen, wie viele Bälle während des Experiments im Fass liegen bleiben. Nach der ersten Halbzeit haben wir 9 Bälle im Fass (denn wir haben 10 hineingetan und dann einen wieder herausgenommen). Nach der zweiten Halbzeit haben wir 18 (wir haben weitere 10 Bälle hinzugefügt und wieder einen herausgenommen). Nach der dritten Halbzeit haben wir 27 Bälle im Fass. Allmählich tritt ein Muster in Erscheinung. Nach der vierten Halbzeit zählen wir 36 Bälle (das heißt 4 X 9); nach der fünften Halbzeit haben wir 45 (5 X 9). Folglich hat nach jeder Halbzeit die Anzahl der Bälle um 9 zugenommen. Eine brillante Vermutung lautet, dass unendlich viele Bälle übrig bleiben, da wir ja unendlich oft neun Bälle hinzufügen. Klingt vernünftig.

Bleiben überhaupt Bälle im Fass? Nehmen wir einmal an, jemand glaubte, es blieben nach Ablauf der Minute ein paar Bälle im Fass liegen. Hmm … Nun, dann kann diese Person doch ins Fass schauen und Bälle darin liegen sehen. Interessant… Also kann diese Person in das Fass hineinlangen und einen herausziehen. Faszinierend … Erinnern Sie sich bitte, dass auf die Kugeloberfläche eines jeden Tischtennisballs eine Zahl gedruckt ist. Auch dieser Ball, den die Person gerade in der Hand hält, hat eine Zahl. Jetzt bitten wir die Person, die Zahl bekannt zu geben. Wir warten. Und warten. Wie könnte die Zahl lauten?

Könnte es die 4 sein? Nein, denn wir wissen ganz genau, dass Ball Nr. 4 bei der vierten Halbzeit entfernt wurde. Könnte es die 17 sein? Auch nicht, weil wir die 17 bei der 17. Halbzeit herausgenommen haben. Wie sieht es mit der 1009 328 aus? Nein, denn dieser Ball wurde bei der 1009 328. Halbzeit herausgenommen. Wie heißt also die Zahl auf dem Ball, der aus dem Fass herausgezogen wurde? Mancher mag Unendlichkeit sagen, aber Unendlichkeit ist keine Zahl, also steht dieses Wort auf keinem Ball. In Wirklichkeit gibt es keine Zahl, die auf diesem angeblichen Ball stehen könnte – denn alle Bälle haben aufgedruckte Zahlen, deshalb kommt hier nur der Fall in Frage, dass keine Bälle übrig geblieben sind. Das Fass ist absolut leer!

Was der Intuition zuwiderläuft, lässt sich der Intuition einverleiben. Die unglaubliche Tatsache, dass keine Bälle im Fass liegen bleiben, scheint unserer Intuition zuwiderzulaufen, was die Notwendigkeit veranschaulicht, unser Denken so fein abzustimmen, dass die Antwort leeres Fass vernünftig klingt. Als Hilfe zur Entwicklung unserer Intuition wollen wir das Szenario ein klein wenig verändern. Angenommen, wir beginnen damit, dass sich bereits alle nummerierten Bälle im Fass befinden und wir bei jeder Halbzeit nur den Ball mit der kleinsten Zahl entfernen. Demnach entfernen wir zur ersten Halbzeit Ball 1, bei der zweiten Halbzeit entfernen wir Ball 2, bei der dritten Halbzeit Ball 3 und so weiter bei unendlich vielen Halbzeiten. In diesem abgeänderten Szenario wird eindeutig ein Ball nach dem anderen entfernt, sodass nach 60 Sekunden (und unendlich vielen Halbzeiten) das Fass völlig leer ist. In gewisser Weise zeigt dieses Szenario, dass die Hin-zufügung von zehn Bällen auf einmal nur ein Ablenkungsmanöver ist. Der wichtigste Punkt, auf den wir uns konzentrieren sollten, ist die systematische Entfernung aller Bälle. Unsere intuitive Auffassung vergleichbarer Größen von Mengen – vor allem unendlicher Mengen – darf sich nur auf die Grundlage von Eins-zu-eins- Entsprechungen stützen. Auch hier erkennen wir eine natürliche Eins-zu-eins-Entsprechung zwischen der Zahl auf dem Ball und der Anzahl der Halbzeiten. Ball 37 entspricht der 37. Halbzeit. Diese Verlagerung des Denkens erfordert sorgfältiges Nachdenken, ist aber der Schlüssel zu unserer vorangegangenen Frage:

Können die Zimmer im Gasthaus zur Unendlichkeit jemals knapp werden? Oder mathematisch anspruchsvoller formuliert: Gibt es eine Unendlichkeit, die größer ist als die Unendlichkeit der Menge aller natürlichen Zahlen? Ist die Unendlichkeit immer Unendlichkeit, oder werden Unendlichkeiten, genau wie Unterwäsche, in unter-schiedlichen Größen ausgeliefert? Weder Mystiker und medial Begabte noch Schneider werden uns bei der Bewältigung dieses unglaublichen Rätsels helfen können. Das Einzige, was wir zur Verfügung haben, ist die grundsätzliche Vorstellung, dass gleiche Größe bedeutet: Es gibt eine Eins-zu-eins-Entsprechung.

Das Ungreifbare begreifen können. Ungeachtet der Details dieser der Intuition zuwiderlaufenden Rätsel ist eines gewiss, wenn es ums Unendliche geht: Mittlerweile können wir auf viel direktere Art und Weise mit der Unendlichkeit umgehen. Wir begannen mit einem vagen Gefühl für etwas Unbegreifliches und verwandelten es in eine konkrete Vorstellung. Als wir uns auf die einfache und vertraute Vorstellung von der Zahl 5 konzentrierten, fanden wir den Schlüssel für die Auseinandersetzung mit dem Unendlichen. Es war zwar kinderleicht, die Finger zusammenzubringen, aber das war der entscheidende Schritt. Obwohl wir noch weit entfernt davon sind, die Konsequenzen erschöpfend erforscht zu haben, die die Vorstellung von der Eins-zu-eins-Entsprechung mit sich bringt, erkennen wir bereits die Kraft, die entsteht, wenn wir dem Verlangen standhalten, uns mit einem Nebel der Unbestimmtheit zufriedenzugeben und uns stattdessen bemühen, das Einfache und Vertraute gründlich zu verstehen.