Das Zusammenwirken von Natur und Zahl – Lotto und Glücksspiele Tipps Teil 2

Das Zusammenwirken von Natur und Zahl – Lotto und Glücksspiele Tipps Teil 1

Demnach offenbaren Fibonacci-Zahlen eine elegante algebraische Einfachheit:

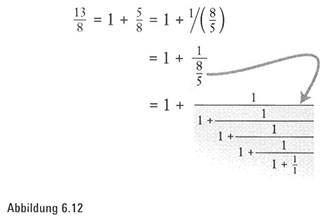
Wir erkennen also, dass das Verhältnis zweier beliebiger aufeinanderfolgender Terme als Kettenbruch langer Divisionen niedergeschrieben werden kann, in denen nur Einsen Vorkommen. Die natürliche Schönheit der Spiralenauszählung lenkte unsere Aufmerksamkeit zuerst auf die fortlaufenden Fibonacci-Zahlen. Inzwischen haben wir herausgefunden, dass diese fortlaufenden Fibonacci-Zahlen eine mathematische Struktur von großer Schönheit erzeugen, die es mit den Spiralen, ihren Gegenstücken in der Natur, aufnehmen kann. Tatsächlich ist diese algebraische Einfachheit eine charakterisierende Eigenschaft. Das heißt, es gibt keine Brüche außer den Verhältnissen aufeinanderfolgender Fibonacci-Zahlen, die als Kettenbrüche ausgedrückt werden können, in denen nur Einsen Vorkommen.

Ausgestattet mit dieser neuen Einsicht, können wir alle diese Einsen zu ihrer diagonalen Formation zusammenfügen, damit sie das Ziel in Angriff nehmen können, auf das alle Brüche hinauslaufen, nämlich die Zahl 1,618 … Wenn wir uns die ständig wachsende Liste der Einsen anschauen, kommen wir zu der Einsicht, dass unser Ziel übereinstimmen muss mit i plus i über i plus i über i plus i über i plus i über i, ad infinitum (Abbildung 6.13).

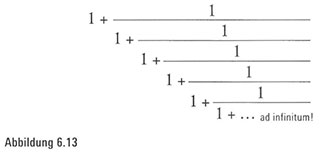
Das heißt, der endlose Dezimalausdruck 1,618 … kann als eine ganz einfache, sich wiederholende Menge von Einsen niedergeschrieben werden, mit dem einzigen Makel, dass die fortlaufende Division unendlich weitergeht.

Wenn wir die Zahl in dieser neuen, nie endenden Form sehen, entdecken wir eine elegante Selbstähnlichkeit. Wenn wir daher einfach einen Rahmen um den endlosen Verlauf der Einsen zeichnen (Abbildung 6.14), dann ist der umrahmte Inhalt eine weitere Kopie der ursprünglichen Zahl! Nennen wir die ursprüngliche Zahl Phi, den griechischen Buchstaben 9, machen wir die Beobachtung, dass

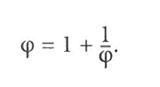
Wenn wir die Gleichung für auflösen, ergibt sich die seltene Gelegenheit, uns an die Algebralektionen aus unserer Schulzeit zu erinnern – wir brauchen nur diese gefürchtete Quadratformel anzuwenden. Aber statt Sie jetzt durch die ganzen langweiligen algebraischen Schritte zu führen, teilen wir Ihnen lediglich mit, dass die positive Antwort so lautet:

Abbildung 6.14: Die Zahl innerhalb des grauen Rahmens ist identisch mit der gesamten Zahl innerhalb des großen schwarzen Rahmens.

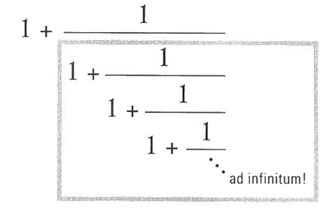
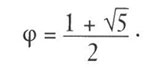
Die Quadratwurzelzahl mag bedrohlich und fremdartig klingen, aber wenn wir (1 + 5)/2 in einen Taschenrechner eingeben, wird folgendes Ergebnis auf dem Display angezeigt: 1,618033989… Unser Taschenrechner bestätigt uns also, dass diese Zahl tatsächlich der Dezimalwert ist, dem die Brüche der fortlaufenden Fibonacci-Zahlen zustreben. Interessant ist die Einsicht, dass es so etwas wie eine kostenlose mathematische Mahlzeit nicht gibt. Obwohl wir in der Lage sind, diese endlose Menge von Einsen in einem sehr gedrängten Ausdruck unterzubringen, hat er seinen Preis: Wir müssen eine Quadratwurzel einführen. In gewisser Hinsicht fängt die Quadratwurzel die unendliche Komplexität der ganzen endlosen Einser-Zipfel auf.

Die Zahl (1 + V5)/2 nennt man Goldener Schnitt, und wie wir im nächsten Kapitel noch entdecken werden, hat diese Zahl die Vorstellungskraft von Künstlern jahrtausendelang herausgefordert. Tatsächlich hat diese Zahl unsere ästhetische Auffassung geprägt, sodass wir uns fragen könnten, ob nicht vielleicht die Mathematik und unsere persönlichen Vorlieben eng miteinander verbunden sind.

Saat ausbringen und ständige Wiederholung ernten
Der endlos sich fortpflanzende Bruch von Einsen, der zum Goldenen Schnitt führt, entsteht aus der endlosen Liste der Fibonacci- Zahlen. Aber die Fibonacci-Zahlen selbst lassen sich in nur zwei Schritten beschreiben. Als Erstes haben wir die beiden Anfangswerte i und i, die wir als Samenkörner betrachten wollen. Und zweitens beschreiben wir den Prozess zur Bildung des nächsten Terms, was bedeutet, dass wir die vorangegangenen zwei Zahlen addieren. Die Samenkörner bilden zusammen mit der Regel die gesamte Fibonacci-Sequenz. Tatsächlich ist diese Sequenz ein Beispiel für eine sogenannte Wiederholungssequenz, weil wir die vorausgegangenen Werte in unserer Zahlenfolge benutzen, um die nächste Zahl zu erzeugen. Wir müssen lediglich die ersten paar Werte und das Verfahren kennen.

Wenn wir auf diese Weise die wesentlichen Bestandteile unseres Konstruktionsprozesses hervorheben, sehen wir, dass es möglich ist, die Fibonacci-Zahlen zu verallgemeinern und selbst noch ausgefallenere Zahlenanordnungen in Betracht zu ziehen, indem wir am Anfang einfach unterschiedliche Samenkörner verwenden. Angenommen, wir begännen mit dem Samenkorn 2 und 1 statt 1 und 1. Was bekämen wir zu sehen, behielten wir denselben Erzeugungsprozess bei, fingen aber mit 2 und 1 an? Die nächste Zahl wäre 2 + 1=3, danach 1 + 3=4 und dann 3 + 4 = 7 und so weiter. Fahren wir auf diese Weise fort, dann sieht die neue Zahlenfolge so aus:
2, 1, 3, 4, 7, 11, 18, 29, 47, 76 …

Diese neue Sequenz hat auch einen Namen; sie wird zu Ehren des französischen Mathematikers Eduard Lucas Lucas-Folge genannt. Er lebte im 19. Jahrhundert und studierte Wiederholungssequenzen.

Die Lucas-Folge hat nicht viel mit der Fibonacci-Sequenz gemeinsam. Nach den ersten paar Termen schon haben wir zwei Listen, die anscheinend völlig unterschiedlich sind.

Fibonacci-Zahlen: 1,2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …
Lucas-Zahlen: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199 …
Auch wenn sie demselben Erzeugungsprozess gehorchen – addieren Sie die beiden vorausgegangenen Zahlen, um die neue Zahl zu erhalten -, scheinen die zustande kommenden Listen nichts miteinander zu tun zu haben, da die Samenkörner am Anfang unterschiedlich sind.

Aber sind die Listen wirklich so unverbunden, wie es scheint?
Wir wollen sehen, wie die Lucas-Zahlen wachsen. Natürlich wissen wir, wie wir dieses Wachstum messen sollten, indem wir nämlich die Verhältnisse der aufeinanderfolgenden Terme und deren entsprechende Dezimalzahlen betrachten (Abbildung 6.15). Wohin werden wir also gelangen?

Überraschung. Es sieht ganz so aus, als befänden wir uns auf dem Weg zum Goldenen Schnitt! Können wir diese Behauptung selbst verifizieren? Natürlich können wir das, und wir wissen auch ganz genau, wie wir dabei vorgehen müssen. Wir schreiben die Verhältnisse fortlaufender Lucas-Zahlen als Kettenbrüche auf und schauen uns an, wohin sie führen (Abbildung 6.16). Schon bald entdecken wir ein fortlaufendes Bruchmuster, das auffällig demjenigen ähnelt, das wir mit den Fibonacci-Zahlen erzeugt haben.

Aber hier erkennen wir nun – statt ausschließlich Einsen zu sehen – lauter Einsen mit Ausnahme der letzten Zahl, die eine Drei ist. Was aber geschähe, wenn wir diesen Prozess unendlich oft wiederholten, wie es erforderlich ist, um den begrenzenden Zielwert

zu finden? Diese letzte 3 würde weiter, weiter und immer weiter in Richtung Unendlichkeit streben. Wiederholten wir also den Vorgang unendlich oft, verschwände die 3 schließlich am Horizont. Wir blieben mit einem endlosen Strom einer 1 plus 1 über 1 plus 1 über 1 plus 1 über 1 plus 1 über 1 ad infinitum zurück – was uns zum Goldenen Schnitt führt.

Also führen beide Wege zum Goldenen Schnitt. Die Entdeckung der Lucas-Folge veranschaulicht eigentlich eine tiefgreifende Strategie zum Verständnis der Suche nach dem Wesentlichen. Welche Merkmale einer Situation sind wirklich wichtig und welche sind irrelevant? Wir haben erkannt, dass die Verhältnisse der fortlaufenden Fibonacci-Zahlen zum Goldenen Schnitt führen und dass die Verhältnisse fortlaufender Lucas-Zahlen ebenfalls zum Goldenen Schnitt führen. Wenn wir uns die Ähnlichkeiten der Parameter anschauen, erkennen wir außerdem eine viel allgemeinere Wahrheit.

Angenommen, wir begännen mit zwei beliebigen Anfangszahlen, die nicht null sind, und erzeugten eine endlose Zahlenliste, für die die Regel gilt, die beiden vorausgegangenen Terme zu addieren, um die nächste Zahl auf der Liste zu erzeugen. Natürlich bringen unterschiedliche Samenkörner am Anfang völlig andere Zahlenfolgen hervor. Allerdings nähern sich, ohne Rücksicht auf den Wert der zu Beginn eingesetzten Samenkörner-, ob klein, ob groß – die Verhältnisse der fortlaufenden Terme zueinander dem Goldenen Schnitt. Das bedeutet, alle diese Wiederholungsprozeduren führen zum Goldenen Schnitt. Die Ausgangswerte sind irrelevant; wichtig ist allein die Prozedur. Hiermit haben wir das Wesentliche herauskristallisiert und das Unwichtige identifiziert.

Zusammenfassung
Die Natur führte uns zu einer Zahlenliste, zu den sogenannten Fibonacci-Zahlen, die uns ihrerseits wiederum dem Goldenen Schnitt näherbrachten. Zuerst erschienen uns jene Zahlen willkürlich und fremdartig. Nachdem wir jedoch den Mustern folgten und den einfachen Dingen auf den Grund gingen, entdeckten wir die überraschende verborgene Schönheit und Struktur, die von Willkürlichkeit weit entfernt sind. Denn innerhalb jeder Zahlensequenz, die wir bilden, indem wir die beiden vorausgegangenen Terme addieren, um die nächste Zahl zu erzeugen, schwirren die nachfolgenden Terme auf den Goldenen Schnitt zu wie die Motten aufs Licht.

Natur und Mathematik überraschen uns mit unerwartetem Zusammenwirken. Wir entdeckten die Fibonacci-Zahlen in unterschiedlichen Blumen und Früchten, während wir den Goldenen Schnitt in unvorhergesehenen Zahlenfolgen fanden. Im nächsten Kapitel richten wir unseren Verstand und unseren Blick auf die visuelle Welt der Geometrie, da wir Widerspiegelungen des Goldenen Schnitts sowohl in der Natur als auch in der Welt der bildenden Kunst finden werden